こんにちはコーヤです。
このページでは、無限が絡む積分を計算する広義積分の計算方法を勉強します。
広義積分の使い所
広義積分は不連続な関数、有界でない関数の積分を計算する方法です。主に無限が絡む以下の2つの場面で使用します。
- 積分区間が無限のとき
- 積分区間内で被積分関数が無限になるとき
それぞれのパターンを見ていきましょう。
パターン1. 積分区間が無限のとき
積分区間に無限があるときは、積分区間をひとまず$R$とおいて計算した後に極限をとります。
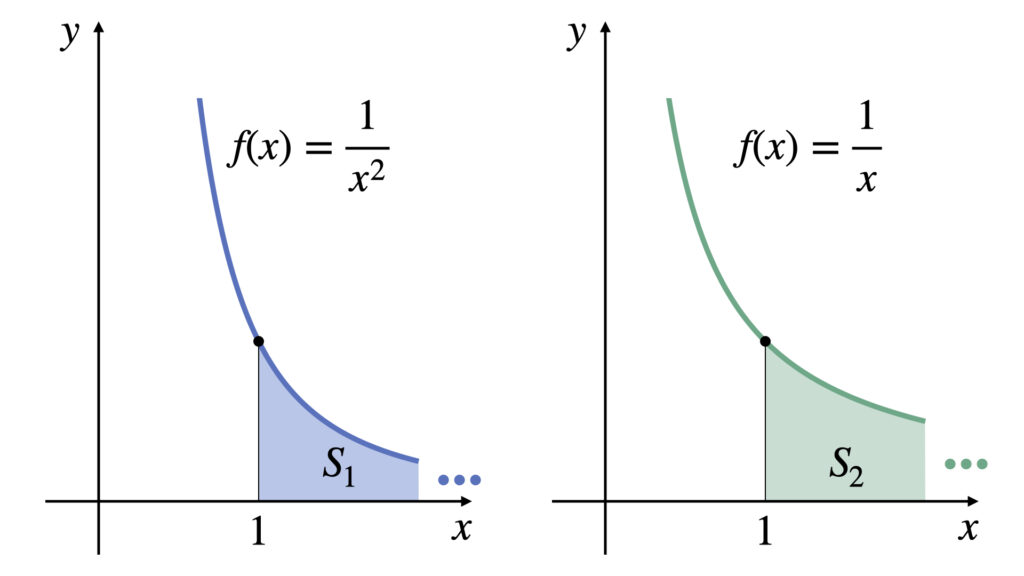
図の色がついた面積$S$を求めます。
$$
\begin{align}
S_1
&=
\displaystyle\int_1^{\infty}
\displaystyle\frac{1}{x^2}
~dx
\\\\&=
\displaystyle\lim_{R\to\infty}
\displaystyle\int_1^R
\displaystyle\frac{1}{x^2}
~dx
\\\\&=
\displaystyle\lim_{R\to\infty}
\left[
-\displaystyle\frac{1}{x}
\right]_1^R
\\\\&=
\displaystyle\lim_{R\to\infty}
\left(
-\displaystyle\frac{1}{R}+1
\right)
\\\\&=
1
\end{align}
$$
$$
\begin{align}
S_2
&=
\displaystyle\int_1^{\infty}
\displaystyle\frac{1}{x}
~dx
\\\\&=
\displaystyle\lim_{R\to\infty}
\displaystyle\int_1^R
\displaystyle\frac{1}{x}
~dx
\\\\&=
\displaystyle\lim_{R\to\infty}
\left[
\log |x|
\right]_1^R
\\\\&=
\displaystyle\lim_{R\to\infty}
\log R
\\\\&=
\infty
\end{align}
$$
$S_1$のように広義積分の値が収束する場合、この広義積分の値は存在し、値は$S_1=1$となります。
$S_2$のように広義積分の値が収束しない場合、この広義積分の値は存在しないとみなします。
パターン2. 積分区間内で被積分関数が無限になるとき
積分区間内で被積分関数が無限になるときは、積分区間をひとまず$r$とおいて計算した後に極限をとります。
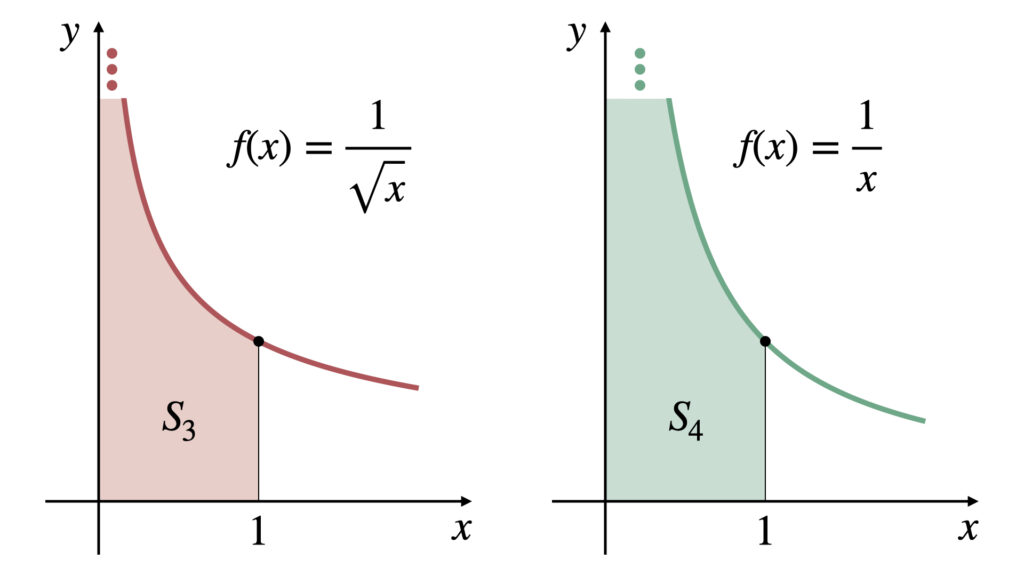
図の色がついた面積$S$を求めます。
$$
\begin{align}
S_3
&=
\displaystyle\int_0^1
\displaystyle\frac{1}{\sqrt{x}}
~dx
\\\\&=
\displaystyle\lim_{r\to +0}
\displaystyle\int_r^1
\displaystyle\frac{1}{\sqrt{x}}
~dx
\\\\&=
\displaystyle\lim_{r\to +0}
\left[
2\sqrt{x}
\right]_r^1
\\\\&=
\displaystyle\lim_{r\to +0}
\left(
2-2\sqrt{r}
\right)
\\\\&=
2
\end{align}
$$
$$
\begin{align}
S_4
&=
\displaystyle\int_0^1
\displaystyle\frac{1}{x}
~dx
\\\\&=
\displaystyle\lim_{r\to +0}
\displaystyle\int_r^1
\displaystyle\frac{1}{x}
~dx
\\\\&=
\displaystyle\lim_{r\to +0}
\left[
\log |x|
\right]_r^1
\\\\&=
\displaystyle\lim_{r\to +0}
-\log r
\\\\&=
\infty
\end{align}
$$
$S_3$のように広義積分の値が収束する場合、この広義積分の値は存在し、値は$S_3=2$となります。
$S_4$のように広義積分の値が収束しない場合、この広義積分の値は存在しないとみなします。
広義積分の収束判定
広義積分が直接計算できない場合は収束判定を行います。
- 積分区間が無限のとき
- 積分区間内で被積分関数が無限になるとき
それぞれのパターンで収束判定の計算が異なります。
パターン1. 積分区間が無限のとき
収束判定の定義
収束判定の定義は以下のとおりです。
区間$[a,\infty)$で連続な関数$f(x)$が$\lambda >1$の定数$\lambda$と$C>0$の定数$C$を用いて、$x\to\infty$のとき
$$
\left|
f(x)x^{\lambda}
\right|
\leq
C
$$
を満たすような$\lambda,C$が存在すれば
$$
\displaystyle\int_a^{\infty}
f(x)
~dx
$$
は絶対収束する。
例題1
$$
S_1
=
\displaystyle\int_1^{\infty}
\displaystyle\frac{1}{x^2}
~dx
$$
が絶対収束するためには、区間$[1,\infty)$で
$$
\left|
x^{\lambda -2}
\right|
\leq
C
$$
を満たせばよいです。例えば
$$
\begin{array}{cc}
\lambda = \displaystyle\frac{3}{2}
&
C = 1
\end{array}
$$
とすると
$$
\left|
x^{\lambda -2}
\right|
=
\left|
\displaystyle\frac{1}{\sqrt{x}}
\right|
$$
となり、$x\to\infty$で
$$
\displaystyle\lim_{x\to\infty}
\left|
\displaystyle\frac{1}{\sqrt{x}}
\right|
\leq
1
$$
となります。
以上より$S_1$は絶対収束します。
例題2
$$
S_2
=
\displaystyle\int_1^{\infty}
\displaystyle\frac{1}{x}
~dx
$$
が絶対収束するためには、区間$[1,\infty)$で
$$
\left|
x^{\lambda -1}
\right|
\leq
C
$$
を満たせばよいですが
$$
\lambda = 1.01
$$
のように$\lambda$をなるべく小さくしても
$$
\left|
x^{\lambda -1}
\right|
=
\left|
x^{\frac{1}{100}}
\right|
$$
となり、$x\to\infty$で
$$
\displaystyle\lim_{x\to\infty}
\left|
x^{\frac{1}{100}}
\right|
=
\infty
$$
となるので、定数$C$をどんな値にしても不等式が成り立ちません。
以上より$S_2$の値は存在しません。
パターン2. 積分区間内で被積分関数が無限になるとき
収束判定の定義
収束判定の定義は以下のとおりです。
区間$(a,b]$で連続な関数$f(x)$が$0<\lambda <1$の定数$\lambda$と$C>0$の定数$C$を用いて、$x\to a+0$のとき
$$
\left|
f(x)(x-a)^{\lambda}
\right|
\leq
C
$$
を満たすような$\lambda,C$が存在すれば
$$
\displaystyle\int_a^b
f(x)
~dx
$$
は絶対収束する。
例題3
$$
S_3
=
\displaystyle\int_0^1
\displaystyle\frac{1}{\sqrt{x}}
~dx
$$
が絶対収束するためには、区間$(0,1]$で
$$
\left|
x^{\lambda -\frac{1}{2}}
\right|
\leq
C
$$
を満たせばよいです。例えば
$$
\begin{array}{cc}
\lambda = \displaystyle\frac{2}{3}
&
C = 1
\end{array}
$$
とすると
$$
\left|
x^{\lambda -\frac{1}{2}}
\right|
=
\left|
x^{\frac{1}{6}}
\right|
$$
となり、$x\to +0$で
$$
\displaystyle\lim_{x\to +0}
\left|
x^{\frac{1}{6}}
\right|
\leq
1
$$
となります。
以上より$S_3$は絶対収束します。
例題4
$$
S_4
=
\displaystyle\int_0^1
\displaystyle\frac{1}{x}
~dx
$$
が絶対収束するためには、区間$(0,1]$で
$$
\left|
x^{\lambda -1}
\right|
\leq
C
$$
を満たせばよいですが
$$
\lambda = 0.99
$$
のように$\lambda$をなるべく大きくしても
$$
\left|
x^{\lambda -1}
\right|
=
\left|
x^{-\frac{1}{100}}
\right|
$$
となり、$x\to +0$で
$$
\displaystyle\lim_{x\to +0}
\left|
x^{-\frac{1}{100}}
\right|
=
\infty
$$
となるので、定数$C$をどんな値にしても不等式が成り立ちません。
以上より$S_4$の値は存在しません。
コーシーの主値
$$
\displaystyle\int_{-\infty}^{\infty}
f(x)
~dx
=
\displaystyle\lim_{R\to\infty}
\displaystyle\int_{-R}^{R}
f(x)
~dx
$$
このように計算するのは間違いです。積分区間の$\infty$と$-\infty$が同じ発散速度かわからないので、1つの文字$R$だけで表すのはNGです。
正しくは
$$
\displaystyle\int_{-\infty}^{\infty}
f(x)
~dx
=
\displaystyle\lim_{R_1\to\infty}
\displaystyle\lim_{R_2\to\infty}
\displaystyle\int_{-R_2}^{R_1}
f(x)
~dx
$$
と2つの文字で計算しないといけません。
例題5
$$
\begin{align}
\displaystyle\int_{-\infty}^{\infty}
2x
~dx
&=
\displaystyle\lim_{R_1\to\infty}
\displaystyle\lim_{R_2\to\infty}
\displaystyle\int_{-R_2}^{R_1}
2x
~dx
\\\\&=
\displaystyle\lim_{R_1\to\infty}
\displaystyle\lim_{R_2\to\infty}
\left[
x^2
\right]_{-R_2}^{R_1}
\\\\&=
\displaystyle\lim_{R_1\to\infty}
\displaystyle\lim_{R_2\to\infty}
\left(
R_1^2-R_2^2
\right)
\end{align}
$$
このように不定形になります。
例題6
$$
\begin{align}
\displaystyle\int_{-1}^{1}
\displaystyle\frac{1}{x}
~dx
&=
\displaystyle\lim_{r_1\to +0}
\displaystyle\lim_{r_2\to +0}
\left(
\displaystyle\int_{-1}^{-r_2}
\displaystyle\frac{1}{x}
~dx
+
\displaystyle\int_{r_1}^{1}
\displaystyle\frac{1}{x}
~dx
\right)
\\\\&=
\displaystyle\lim_{r_1\to +0}
\displaystyle\lim_{r_2\to +0}
\left(
\left[
\log |x|
\right]_{-1}^{-r_2}
+
\left[
\log |x|
\right]_{r_1}^{1}
\right)
\\\\&=
\displaystyle\lim_{r_1\to +0}
\displaystyle\lim_{r_2\to +0}
\left(
\log r_2 -\log r_1
\right)
\\\\&=
\displaystyle\lim_{r_1\to +0}
\displaystyle\lim_{r_2\to +0}
\log
\displaystyle\frac{r_2}{r_1}
\end{align}
$$
これも不定形になります。
上記の例題5,6のように、広義積分は2つの文字を使うと値を計算できなくなることが多いです。
これを解消するために「コーシーの主値」という特別ルールを採用する場合があります。
例題5のように積分区間が$(-\infty,\infty)$の場合、同じくらいの発散速度だと仮定して$(-R,R)$として計算します。
例題6のように被積分関数が$x=0$で定義されていない場合、積分区間が同じくらい定義域から離れている仮定して$(-1,-r)$と$(r,1)$として計算します。
この特別ルールで積分の値を計算する場合はインテグラルの前に$PV$をつけて表します。
例題5(コーシーの主値)
$$
\begin{align}
PV
\displaystyle\int_{-\infty}^{\infty}
2x
~dx
&=
\displaystyle\lim_{R\to\infty}
\displaystyle\int_{-R}^{R}
2x
~dx
\\\\&=
\displaystyle\lim_{R\to\infty}
\left[
x^2
\right]_{-R}^{R}
\\\\&=
\displaystyle\lim_{R\to\infty}
\left(
R^2-R^2
\right)
\\\\&=
0
\end{align}
$$
例題6(コーシーの主値)
$$
\begin{align}
PV
\displaystyle\int_{-1}^{1}
\displaystyle\frac{1}{x}
~dx
&=
\displaystyle\lim_{r\to +0}
\left(
\displaystyle\int_{-1}^{-r}
\displaystyle\frac{1}{x}
~dx
+
\displaystyle\int_{r}^{1}
\displaystyle\frac{1}{x}
~dx
\right)
\\\\&=
\displaystyle\lim_{r\to +0}
\left(
\left[
\log |x|
\right]_{-1}^{_2}
+
\left[
\log |x|
\right]_{r}^{1}
\right)
\\\\&=
\displaystyle\lim_{r\to +0}
\left(
\log r -\log r
\right)
\\\\&=
0
\end{align}
$$
このようにコーシーの主値を使うと値が求まります。

$PV$は主値(Principal Value)のことです。
置換積分と広義積分の相性
置換積分を駆使しながら積分値を求めるとき、広義積分で使う$R$や$r$が邪魔して置換が上手く行かない場合があります。
$$
\displaystyle\int_{-\infty}^{\infty}
e^{-x^2}
~dx
$$
$$
\displaystyle\int_{0}^{\frac{1}{2}\pi}
\log(\sin x)
~dx
$$
こういった積分です。
こういう場合は最初に収束判定を行うと計算しやすくなります。収束すると分かれば
- $R$や$r$を使わずに計算できる
- 積分値を$I$など文字をつかって表現できる
といったメリットがあります。
計算過程を実際に見たほうがメリットが伝わると思うので、上記2つの積分を解いているページをご覧ください。1つ目の例はガウス積分のページ、2つ目の例は積分腕試しのページで解いています。
まとめ
- 積分区間が無限のとき
- 積分区間内で被積分関数が無限になるとき
このような場合は広義積分で計算します。






コメント欄