こんにちはコーヤです。
このページでは、回転体の体積と表面積の計算方法を勉強します。陽関数表示、媒介変数表示、極座標表示の3パターンです。
回転体の体積と表面積の公式
陽関数表示、媒介変数表示、極座標表示の3パターンにおいて、回転体の体積$V$と表面積$S$を以下のように決めます。
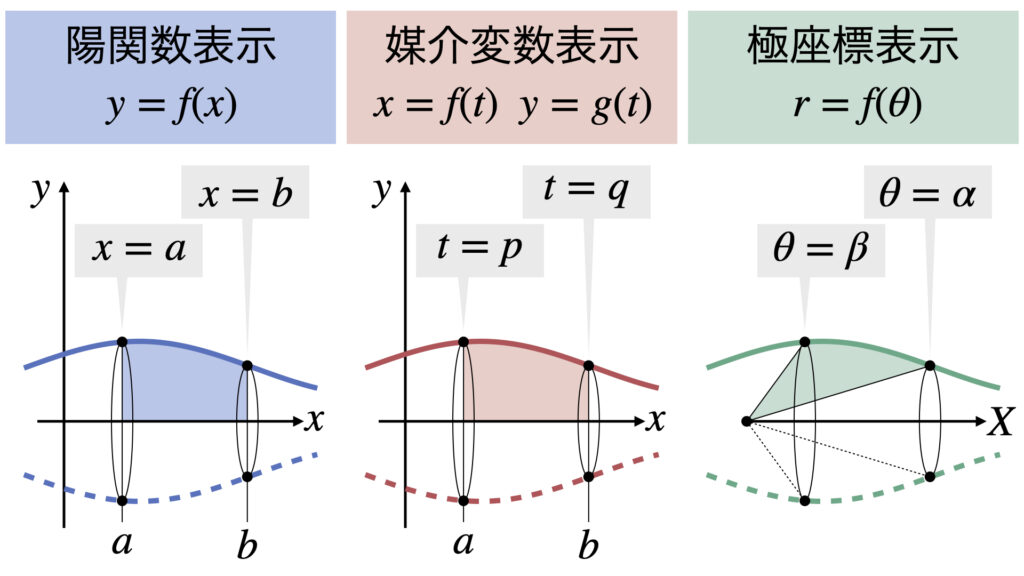
それぞれの表示形式において$x$軸で回転させた時の回転体の体積$V$と表面積$S$とし、体積$V$と表面積$S$の公式は以下の式です。
陽関数表示の公式
$$
\begin{align}
V
&=
\pi
\displaystyle\int_a^b
f(x)^2
~dx
\\\\
S
&=
2\pi
\displaystyle\int_a^b
f(x)\sqrt{1+f'(x)^2}
~dx
\end{align}
$$
媒介変数表示の公式
$$
\begin{align}
V
&=
\pi
\displaystyle\int_p^q
f'(t)g(t)^2
~dt
\\\\
S
&=
2\pi
\displaystyle\int_p^q
g(t)\sqrt{f'(t)^2+g'(t)^2}
~dt
\end{align}
$$
極座標表示の公式
$$
\begin{align}
V
&=
\displaystyle\frac{2}{3}\pi
\displaystyle\int_{\alpha}^{\beta}
f(\theta)^3\sin\theta
~d\theta
\\\\
S
&=
2\pi
\displaystyle\int_{\alpha}^{\beta}
f(\theta)\sin\theta\sqrt{f(\theta)^2+f'(\theta)^2}
~d\theta
\end{align}
$$
それでは例題で計算しましょう。
回転体の体積と表面積の例題
陽関数表示の例題
$$
\begin{array}{cc}
y=f(x)=\cosh x
&
(0\leq x\leq \log 2)
\end{array}
$$
この関数を$x$軸まわりで回転させた回転体の体積$V$と表面積$S$を計算します。
まずは体積$V$の計算です。
$$
\begin{align}
V
&=
\pi
\displaystyle\int_0^{\log 2}
f(x)^2
~dx
\\\\&=
\pi
\displaystyle\int_0^{\log 2}
\cosh^2 x
~dx
\\\\&=
\displaystyle\frac{1}{2}\pi
\displaystyle\int_0^{\log 2}
\cosh 2x+1
~dx
\\\\&=
\displaystyle\frac{1}{2}\pi
\left[
\displaystyle\frac{1}{2}\sinh 2x+x
\right]_0^{\log 2}
\\\\&=
\displaystyle\frac{1}{2}\pi
\left\{
\displaystyle\frac{1}{2}\sinh (2\log 2)+\log 2
\right\}
\\\\&=
\displaystyle\frac{1}{2}\pi
\left(
\displaystyle\frac{15}{16}+\log 2
\right)
\end{align}
$$
次に表面積$S$の計算です。
$$
f'(x)
=
\sinh x
$$
より
$$
\begin{align}
S
&=
2\pi
\displaystyle\int_0^{\log 2}
f(x)\sqrt{1+f'(x)^2}
~dx
\\\\&=
2\pi
\displaystyle\int_0^{\log 2}
\cosh x\sqrt{1+\sinh^2 x}
~dx
\\\\&=
2\pi
\displaystyle\int_0^{\log 2}
\cosh x\sqrt{\cosh^2 x}
~dx
\\\\&=
2\pi
\displaystyle\int_0^{\log 2}
\cosh x|\cosh x|
~dx
\\\\&=
2\pi
\displaystyle\int_0^{\log 2}
\cosh^2 x
~dx
\\\\&=
\pi
\left(
\displaystyle\frac{15}{16}+\log 2
\right)
\end{align}
$$
途中の絶対値が出てくる式は、$0\leq x\leq \log 2$の範囲で$\cosh x >0$なので絶対値が外れます。
最後の積分計算は体積$V$と同じ積分なので計算過程を省略しました。
媒介変数表示の例題
$$
\begin{array}{cc}
\begin{array}{l}
x=f(t)=t-\sin t
\\
y=g(t)=1-\cos t
\end{array}
&
(0\leq t\leq 2\pi)
\end{array}
$$
この関数を$x$軸まわりで回転させた回転体の体積$V$と表面積$S$を計算します。サイクロイドと呼ばれる関数です。
まずは体積$V$の計算です。
$$
f'(t)
=
1-\cos t
$$
より
$$
\begin{align}
V
&=
\pi
\displaystyle\int_0^{2\pi}
f'(t)g(t)^2
~dt
\\\\&=
\pi
\displaystyle\int_0^{2\pi}
(1-\cos t)(1-\cos t)^2
~dt
\\\\&=
\pi
\displaystyle\int_0^{2\pi}
1-3\cos t+3\cos^2 t-\cos^3 t
~dt
\\\\&=
\pi
\displaystyle\int_0^{2\pi}
\displaystyle\frac{5}{2}-\displaystyle\frac{15}{4}\cos t+\displaystyle\frac{3}{2}\cos 2t-\displaystyle\frac{1}{4}\cos 3t
~dt
\\\\&=
\pi
\left[
\displaystyle\frac{5}{2}t-\displaystyle\frac{15}{4}\sin t+\displaystyle\frac{3}{4}\sin 2t-\displaystyle\frac{1}{12}\sin 3t
\right]_0^{2\pi}
\\\\&=
5\pi^2
\end{align}
$$
次に表面積$S$の計算です。
$$
g'(t)
=
\sin t
$$
より
$$
\begin{align}
S
&=
2\pi
\displaystyle\int_0^{2\pi}
g(t)\sqrt{f'(t)^2+g'(t)^2}
~dt
\\\\&=
2\pi
\displaystyle\int_0^{2\pi}
(1-\cos t)\sqrt{(1-\cos t)^2+\sin ^2t}
~dt
\\\\&=
2\pi
\displaystyle\int_0^{2\pi}
(1-\cos t)\sqrt{2(1-\cos t)}
~dt
\\\\&=
2\sqrt{2}\pi
\displaystyle\int_0^{2\pi}
(1-\cos t)^{\frac{3}{2}}
~dt
\\\\&=
2\sqrt{2}\pi
\displaystyle\int_0^{2\pi}
\left(
2\sin^2\displaystyle\frac{t}{2}
\right)^{\frac{3}{2}}
~dt
\\\\&=
8\pi
\displaystyle\int_0^{2\pi}
\sin^3\displaystyle\frac{t}{2}
~dt
\\\\&=
8\pi
\displaystyle\int_0^{2\pi}
\left(
1-\cos^2 \displaystyle\frac{t}{2}
\right)
\sin\displaystyle\frac{t}{2}
~dt
\end{align}
$$
変数を$t$から$u$へ置換します。
$$
\begin{align}
u&=\cos \displaystyle\frac{t}{2}
\\\\
du&=-\displaystyle\frac{1}{2}\sin \displaystyle\frac{t}{2} ~dt
\end{align}
$$
$$
\begin{array}{ccccc}
t & : & 0 & \to & 2\pi
\\\\
u & : & 1 & \to & -1
\end{array}
$$
よって
$$
\begin{align}
8\pi
\displaystyle\int_0^{2\pi}
\left(
1-\cos^2 \displaystyle\frac{t}{2}
\right)
\sin\displaystyle\frac{t}{2}
~dt
&=
8\pi
\displaystyle\int_1^{-1}
(1-u^2)(-2)
~du
\\\\&=
16\pi
\displaystyle\int_{-1}^{1}
1-u^2
~du
\\\\&=
16\pi
\left[
u-\displaystyle\frac{1}{3}u^3
\right]_{-1}^1
\\\\&=
\displaystyle\frac{64}{3}\pi
\end{align}
$$
となります。
極座標表示の例題
$$
\begin{array}{cc}
r=f(\theta)=1+\cos\theta
&
(0\leq \theta\leq \pi)
\end{array}
$$
この関数を始線$X$まわりで回転させた回転体の体積$V$と表面積$S$を計算します。カージオイドと呼ばれる関数です。
まずは体積$V$の計算です。
$$
\begin{align}
V
&=
\displaystyle\frac{2}{3}\pi
\displaystyle\int_{0}^{\pi}
f(\theta)^3\sin\theta
~d\theta
\\\\&=
\displaystyle\frac{2}{3}\pi
\displaystyle\int_{0}^{\pi}
(1+\cos\theta)^3\sin\theta
~d\theta
\end{align}
$$
変数を$\theta$から$t$へ置換します。
$$
\begin{align}
t&=\cos \theta
\\\\
dt&=-\sin\theta ~d\theta
\end{align}
$$
$$
\begin{array}{ccccc}
\theta & : & 0 & \to & \pi
\\\\
t & : & 1 & \to & -1
\end{array}
$$
よって
$$
\begin{align}
\displaystyle\frac{2}{3}\pi
\displaystyle\int_{0}^{\pi}
(1+\cos\theta)^3\sin\theta
~d\theta
&=
\displaystyle\frac{2}{3}\pi
\displaystyle\int_{1}^{-1}
(1+t^3)(-1)
~dt
\\\\&=
\displaystyle\frac{2}{3}\pi
\displaystyle\int_{-1}^{1}
1+t^3
~dt
\\\\&=
\displaystyle\frac{2}{3}\pi
\left[
\displaystyle\frac{1}{4}(1+t)^4
\right]_{-1}^{1}
\\\\&=
\displaystyle\frac{8}{3}\pi
\end{align}
$$
次に表面積$S$の計算です。
$$
f'(\theta)
=
-\sin\theta
$$
より
$$
\begin{align}
S
&=
2\pi
\displaystyle\int_{0}^{\pi}
f(\theta)\sin\theta\sqrt{f(\theta)^2+f'(\theta)^2}
~d\theta
\\\\&=
2\pi
\displaystyle\int_{0}^{\pi}
(1+\cos\theta)\sin\theta\sqrt{(1+\cos\theta)^2+(-\sin\theta)^2}
~d\theta
\\\\&=
2\pi
\displaystyle\int_{0}^{\pi}
(1+\cos\theta)\sin\theta\sqrt{2(1+\cos\theta)}
~d\theta
\\\\&=
2\sqrt{2}\pi
\displaystyle\int_{0}^{\pi}
(1+\cos\theta)^{\frac{3}{2}}\sin\theta
~d\theta
\end{align}
$$
変数を$\theta$から$t$へ置換します。
$$
\begin{align}
t&=\cos \theta
\\\\
dt&=-\sin\theta ~d\theta
\end{align}
$$
$$
\begin{array}{ccccc}
\theta & : & 0 & \to & \pi
\\\\
t & : & 1 & \to & -1
\end{array}
$$
よって
$$
\begin{align}
2\sqrt{2}\pi
\displaystyle\int_{0}^{\pi}
(1+\cos\theta)^{\frac{3}{2}}\sin\theta
~d\theta
&=
2\sqrt{2}\pi
\displaystyle\int_{1}^{-1}
(1+t)^{\frac{3}{2}}(-1)
~dt
\\\\&=
2\sqrt{2}\pi
\displaystyle\int_{-1}^{1}
(1+t)^{\frac{3}{2}}
~dt
\\\\&=
2\sqrt{2}\pi
\left[
\displaystyle\frac{2}{5}(1+t)^{\frac{5}{2}}
\right]_{-1}^{1}
\\\\&=
\displaystyle\frac{32}{5}\pi
\end{align}
$$
となります。
極座標表示の回転体の注意点
同じ曲線でも、陽関数表示(もしくは媒介変数表示)で回転させた場合と極座標表示で回転させた場合で形が異なります。
単位円の$\displaystyle\frac{1}{4}\pi$から$\displaystyle\frac{1}{2}\pi$の曲線を、それぞれ陽関数表示と極座標表示で回転させて体積$V$と表面積$S$を求めてみます。

この曲線を陽関数表示と極座標表示で表すと以下のようになります。
$$
\begin{array}{lll}
f(x)=\sqrt{1-x^2}
&&
\left( 0 \leq x \leq \displaystyle\frac{1}{\sqrt{2}} \right)
\\\\
f(\theta)=1
&&
\left( \displaystyle\frac{1}{4}\pi \leq x \leq \displaystyle\frac{1}{2}\pi \right)
\end{array}
$$
陽関数表示の体積と表面積
$$
\begin{align}
V
&=
\pi
\displaystyle\int_a^b
f(x)^2
~dx
\\\\&=
\pi
\displaystyle\int_0^{\frac{1}{\sqrt{2}}}
1-x^2
~dx
\\\\&=
\pi
\left[
x-\displaystyle\frac{1}{3}x^3
\right]_{0}^{\frac{1}{\sqrt{2}}}
\\\\&=
\displaystyle\frac{5\sqrt{2}}{12}\pi
\end{align}
$$
$$
\begin{align}
S
&=
2\pi
\displaystyle\int_a^b
f(x)\sqrt{1+f'(x)^2}
~dx
\\\\&=
2\pi
\displaystyle\int_0^{\frac{1}{\sqrt{2}}}
\sqrt{1-x^2}\displaystyle\frac{1}{\sqrt{1-x^2}}
~dx
\\\\&=
2\pi
\displaystyle\int_0^{\frac{1}{\sqrt{2}}}
~dx
\\\\&=
2\pi
\left[
x
\right]_{0}^{\frac{1}{\sqrt{2}}}
\\\\&=
\sqrt{2}\pi
\end{align}
$$
極座標表示の体積と表面積
$$
\begin{align}
V
&=
\displaystyle\frac{2}{3}\pi
\displaystyle\int_{\alpha}^{\beta}
f(\theta)^3\sin\theta
~d\theta
\\\\&=
\displaystyle\frac{2}{3}\pi
\displaystyle\int_{\frac{1}{4}\pi}^{\frac{1}{2}\pi}
\sin\theta
~d\theta
\\\\&=
\displaystyle\frac{2}{3}\pi
\left[
\cos\theta
\right]_{\frac{1}{4}\pi}^{\frac{1}{2}\pi}
\\\\&=
\displaystyle\frac{\sqrt{2}}{3}\pi
\\\\&=
\displaystyle\frac{4\sqrt{2}}{12}\pi
\end{align}
$$
$$
\begin{align}
S
&=
2\pi
\displaystyle\int_{\alpha}^{\beta}
f(\theta)\sin\theta\sqrt{f(\theta)^2+f'(\theta)^2}
~d\theta
\\\\&=
2\pi
\displaystyle\int_{\frac{1}{4}\pi}^{\frac{1}{2}\pi}
\sin\theta
~d\theta
\\\\&=
2\pi
\left[
\cos\theta
\right]_{\frac{1}{4}\pi}^{\frac{1}{2}\pi}
\\\\&=
\sqrt{2}\pi
\end{align}
$$
結果を比較すると、表面積は同じですが体積は異なります。なぜでしょうか。
体積が異なる理由

体積が異なる理由は回転している領域が異なるからです。
陽関数表示のときは図の$A_1,A_2$の部分が回転します。極座標表示のときは図の$A_1$が回転します。
したがって$A_2$の回転体の体積だけ差が出ることになります。
$A_2$の回転体は、底面が半径$\displaystyle\frac{1}{\sqrt{2}}$の円、高さ$\displaystyle\frac{1}{\sqrt{2}}$の円錐なのでその体積は
$$
V=\displaystyle\frac{\sqrt{2}}{12}\pi
$$
となります。陽関数表示と極座標表示の体積の差と一致しています。
表面積が一致する理由
表面積が一致する理由は、どちらの表示形式でも図の曲線$L$の部分が回転した表面積だからです。
体積や表面積の導出過程が気になった方は、以下の公式の導出をご覧ください。
公式の導出
それぞれの公式の導出を行います。
陽関数表示の公式の導出
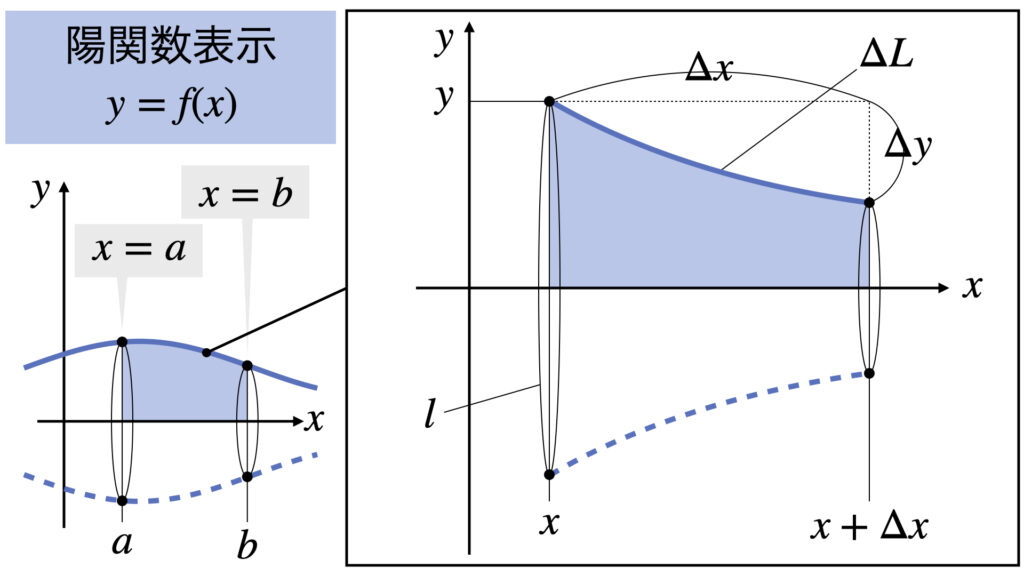
まず体積$V$の公式を導出します。
$\Delta V$を円柱だと近似して、底面の半径$y$で高さ$\Delta x$の円柱の体積を求めると
$$
\Delta V
\simeq
\pi y^2\Delta x
$$
$\Delta x$を移項して
$$
\displaystyle\frac{\Delta V}{\Delta x}
\simeq
\pi y^2
$$
ここで$\Delta x\to 0$のとき
$$
\displaystyle\frac{dV}{dx}
=
\pi y^2
$$
両辺を$a\leq x\leq b$の範囲の$x$で積分して
$$
V
=
\pi
\displaystyle\int_a^b
y^2
~dx
$$
となります。
次に表面積$S$の公式を導出します。
半径$y$の円の周長$l$は
$$
l
=
2\pi y
$$
これに曲線の長さ$\Delta L$をかけて、表面積$\Delta S$は
$$
\Delta S
\simeq
2\pi y\Delta L
$$
ここで三平方の定理より
$$
\begin{align}
\Delta L
&\simeq
\sqrt{(\Delta x)^2+(\Delta y)^2}
\\\\&=
\sqrt{1+\left(\displaystyle\frac{\Delta y}{\Delta x}\right)^2}
\Delta x
\end{align}
$$
よって
$$
\Delta S
\simeq
2\pi y
\sqrt{1+\left(\displaystyle\frac{\Delta y}{\Delta x}\right)^2}
\Delta x
$$
$\Delta x$を移項して
$$
\displaystyle\frac{\Delta S}{\Delta x}
\simeq
2\pi y
\sqrt{1+\left(\displaystyle\frac{\Delta y}{\Delta x}\right)^2}
$$
ここで$\Delta x\to 0$のとき
$$
\displaystyle\frac{dS}{dx}
=
2\pi y
\sqrt{1+\left(\displaystyle\frac{dy}{dx}\right)^2}
$$
両辺を$a\leq x\leq b$の範囲の$x$で積分して
$$
S
=
2\pi
\displaystyle\int_a^b
y\sqrt{1+\left(\displaystyle\frac{dy}{dx}\right)^2}
~dx
$$
となります。
媒介変数表示の公式の導出
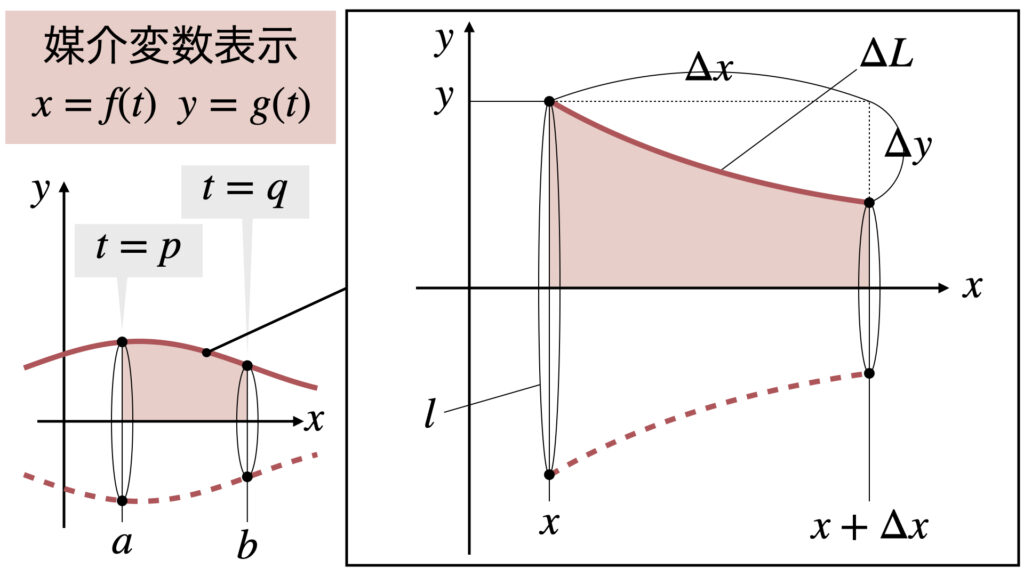
体積$V$の公式は陽関数の公式の変数を$x=f(t)$と置換すれば求まります。
$$
\begin{align}
V
&=
\pi
\displaystyle\int_a^b
y^2
~dx
\\\\&=
\pi
\displaystyle\int_p^q
y^2
\displaystyle\frac{dx}{dt}
~dt
\end{align}
$$
表面積$S$の公式も陽関数のときと同じような計算です。
半径$y$の円の周長$l$は
$$
l
=
2\pi y
$$
これに曲線の長さ$\Delta L$をかけて、表面積$\Delta S$は
$$
\Delta S
\simeq
2\pi y\Delta L
$$
ここで三平方の定理より
$$
\begin{align}
\Delta L
&\simeq
\sqrt{(\Delta x)^2+(\Delta y)^2}
\\\\&=
\sqrt{\left(\displaystyle\frac{\Delta x}{\Delta t}\right)^2+\left(\displaystyle\frac{\Delta y}{\Delta t}\right)^2}
\Delta t
\end{align}
$$
よって
$$
\Delta S
\simeq
2\pi y
\sqrt{\left(\displaystyle\frac{\Delta x}{\Delta t}\right)^2+\left(\displaystyle\frac{\Delta y}{\Delta t}\right)^2}
\Delta t
$$
$\Delta t$を移項して
$$
\displaystyle\frac{\Delta S}{\Delta t}
\simeq
2\pi y
\sqrt{\left(\displaystyle\frac{\Delta x}{\Delta t}\right)^2+\left(\displaystyle\frac{\Delta y}{\Delta t}\right)^2}
$$
ここで$\Delta t\to 0$のとき
$$
\displaystyle\frac{dS}{dx}
=
2\pi y
\sqrt{\left(\displaystyle\frac{dx}{dt}\right)^2+\left(\displaystyle\frac{dy}{dt}\right)^2}
$$
両辺を$p\leq t\leq q$の範囲の$t$で積分して
$$
S
=
2\pi
\displaystyle\int_p^q
y\sqrt{\left(\displaystyle\frac{dx}{dt}\right)^2+\left(\displaystyle\frac{dy}{dt}\right)^2}~dt
$$
となります。
極座標表示の公式の導出
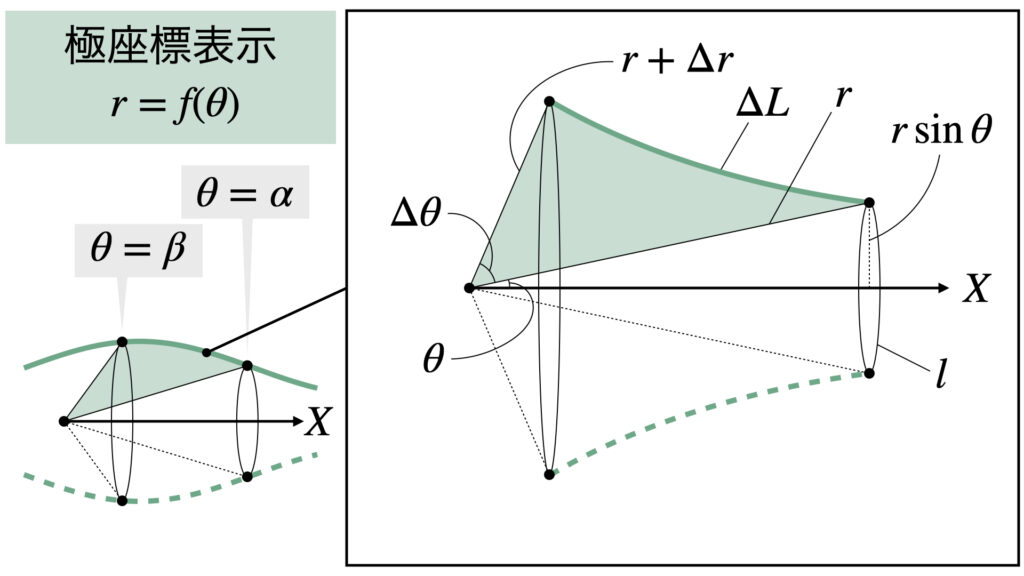
まず体積$V$の公式を導出します。
極座標平面の領域を回転させると計算が大変なので、回転させる前に直交座標に直します。
極座標中の点$(r,\theta)$と点$(r+\Delta r,\theta +\Delta\theta)$を直交座標に直すと
$$
\begin{array}{lll}
(r,\theta)
& \to &
(r\cos\theta,r\sin\theta)
\\\\
(r+\Delta r,\theta +\Delta\theta)
& \to &
((r+\Delta r)\cos(\theta +\Delta\theta),(r+\Delta r)\sin(\theta +\Delta\theta))
\end{array}
$$
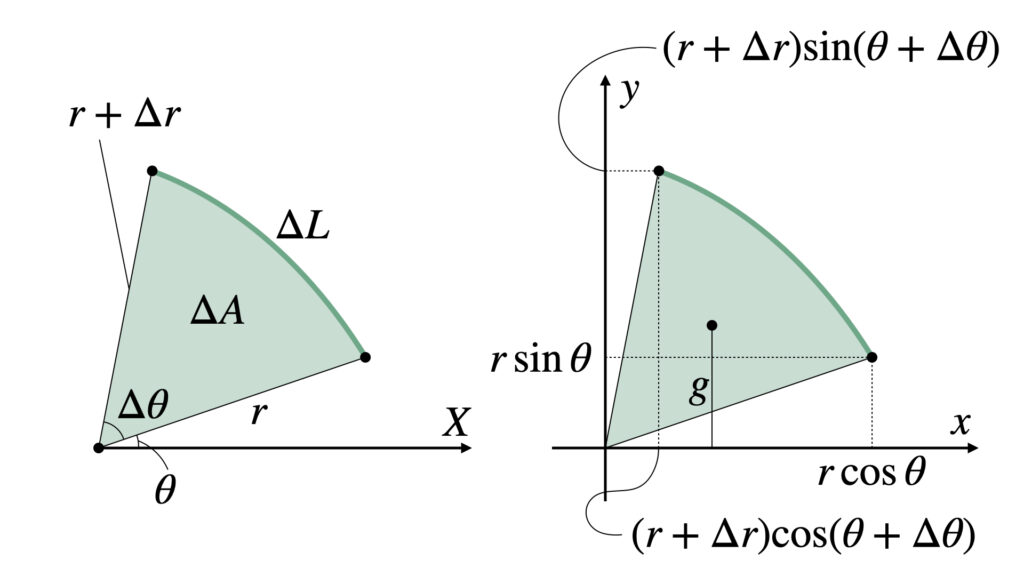
となります。
図の$\Delta A$は三角形の面積だと近似して
$$
\Delta A
\simeq
\displaystyle\frac{1}{2}
r(r+\Delta r)\sin\Delta\theta
$$
また、三角形の重心と$x$軸との距離$g$は
$$
g
\simeq
\displaystyle\frac{1}{3}
\left\{
r\sin\theta+(r+\Delta r)\sin(\theta+\Delta\theta)
\right\}
$$
ここでパップスギュルダンの定理より

パップスギュルダンの定理は平面図形を回転させた回転体の体積を求める定理です。
「平面図形の面積」と「平面図形の重心が回転で移動する距離」の積が回転体の体積となります。
今の例だと「平面図形の面積」は$\Delta A$で「平面図形の重心が回転で移動する距離」が$2\pi g$です。
$$
\begin{align}
\Delta V
&\simeq
2\pi g\Delta A
\\\\&=
\displaystyle\frac{1}{3}
\pi
\left\{
r\sin\theta+(r+\Delta r)\sin(\theta+\Delta\theta)
\right\}
r(r+\Delta r)\sin\Delta\theta
\end{align}
$$
となります。
両辺を$\Delta \theta$で割って
$$
\displaystyle\frac{\Delta V}{\Delta\theta}
\simeq
\displaystyle\frac{1}{3}
\pi
\left\{
r\sin\theta+(r+\Delta r)\sin(\theta+\Delta\theta)
\right\}
r(r+\Delta r)
\displaystyle\frac{\sin\Delta\theta}{\Delta\theta}
$$
ここで$\Delta \theta\to 0$のとき$\Delta r\to 0$なので
$$
\begin{align}
\displaystyle\frac{dV}{d\theta}
&=
\displaystyle\frac{1}{3}
\pi
\left\{
r\sin\theta+r\sin\theta
\right\}
r\cdot r\cdot 1
\\\\&=
\displaystyle\frac{2}{3}
\pi
r^3\sin\theta
\end{align}
$$
両辺を$\alpha\leq \theta\leq \beta$の範囲の$\theta$で積分して
$$
V
=
\displaystyle\frac{2}{3}
\pi
\displaystyle\int_{\alpha}^{\beta}
r^3\sin\theta
~d\theta
$$
となります。
次に表面積$S$の公式を導出します。陽関数のときと同じような計算です。
半径$r\sin\theta$の円の周長$l$は
$$
l
=
2\pi r\sin\theta
$$
これに曲線の長さ$\Delta L$をかけて、表面積$\Delta S$は
$$
\Delta S
\simeq
2\pi r\sin\theta\Delta L
$$
両辺$\Delta\theta$で割って
$$
\displaystyle\frac{\Delta S}{\Delta\theta}
\simeq
2\pi r\sin\theta\displaystyle\frac{\Delta L}{\Delta\theta}
$$
となります。ここで余弦定理より
$$
\begin{align}
(\Delta L)^2
&\simeq
r^2+(r+\Delta r)^2-2r(r+\Delta r)\cos\Delta\theta
\\\\&=
2r^2+2r\Delta r+(\Delta r)^2-(2r^2+2r\Delta r)\cos\Delta\theta
\\\\&=
(2r^2+2r\Delta r)(1-\cos\Delta\theta)+(\Delta r)^2
\\\\&=
2r(r+\Delta r)(1-\cos\Delta\theta)+(\Delta r)^2
\end{align}
$$
両辺を$(\Delta\theta)^2$で割って
$$
\left(
\displaystyle\frac{\Delta L}{\Delta\theta}
\right)^2
\simeq
2r(r+\Delta r)
\displaystyle\frac{(1-\cos\Delta\theta)}{(\Delta\theta)^2}
+
\left(
\displaystyle\frac{\Delta r}{\Delta\theta}
\right)^2
$$
ルートを使って
$$
\displaystyle\frac{\Delta L}{\Delta\theta}
\simeq
\sqrt{
2r(r+\Delta r)
\displaystyle\frac{(1-\cos\Delta\theta)}{(\Delta\theta)^2}
+
\left(
\displaystyle\frac{\Delta r}{\Delta\theta}
\right)^2
}
$$
となります。
ルートを使いましたが
$$
\displaystyle\frac{\Delta L}{\Delta\theta}
\simeq
\pm
\sqrt{
2r(r+\Delta r)
\displaystyle\frac{(1-\cos\Delta\theta)}{(\Delta\theta)^2}
+
\left(
\displaystyle\frac{\Delta r}{\Delta\theta}
\right)^2
}
$$
のように$\pm$は付きません。
極座標表示なので$r\geq 0$かつ$\Delta r\geq 0$です。よって
$$
2r(r+\Delta r)
\geq
0
$$
となり、この項はプラスです。
次に$-1\leq \cos\Delta\theta\leq 1$より
$$
1-\cos\Delta\theta
\geq
0
$$
となり、この項もプラスです。
残ってる項は2乗されているのでプラスです。
ルートの中身が全てプラスなので、ルートの外の符号はプラマイではなくプラスになります。
この結果を代入して
$$
\begin{align}
\displaystyle\frac{\Delta S}{\Delta\theta}
&\simeq
2\pi r\sin\theta\displaystyle\frac{\Delta L}{\Delta\theta}
\\\\&=
2\pi r\sin\theta
\sqrt{
2r(r+\Delta r)
\displaystyle\frac{(1-\cos\Delta\theta)}{(\Delta\theta)^2}
+
\left(
\displaystyle\frac{\Delta r}{\Delta\theta}
\right)^2
}
\end{align}
$$
ここで$\Delta \theta\to 0$のとき$\Delta r\to 0$なので
$$
\begin{align}
\displaystyle\frac{dS}{d\theta}
&=
2\pi r\sin\theta
\sqrt{
2r\cdot r \cdot
\displaystyle\frac{1}{2}
+
\left(
\displaystyle\frac{dr}{d\theta}
\right)^2
}
\\\\&=
2\pi r\sin\theta
\sqrt{
r^2
+
\left(
\displaystyle\frac{dr}{d\theta}
\right)^2
}
\end{align}
$$
両辺を$\alpha\leq \theta\leq \beta$の範囲の$\theta$で積分して
$$
S
=
2\pi
\displaystyle\int_{\alpha}^{\beta}
r\sin\theta\sqrt{r^2+\left(\displaystyle\frac{dr}{d\theta}\right)^2}
~d\theta
$$
となります。
まとめ
陽関数表示、媒介変数表示、極座標表示の3パターンにおいて、回転体の体積$V$と表面積$S$を以下のように決めます。

このとき、それぞれの表示形式において体積$V$と表面積$S$の公式は以下の式です。
陽関数表示
$$
\begin{align}
V
&=
\pi
\displaystyle\int_a^b
f(x)^2
~dx
\\\\
S
&=
2\pi
\displaystyle\int_a^b
f(x)\sqrt{1+f'(x)^2}
~dx
\end{align}
$$
媒介変数表示
$$
\begin{align}
V
&=
\pi
\displaystyle\int_p^q
f'(t)g(t)^2
~dt
\\\\
S
&=
2\pi
\displaystyle\int_p^q
g(t)\sqrt{f'(t)^2+g'(t)^2}
~dt
\end{align}
$$
極座標表示
$$
\begin{align}
V
&=
\displaystyle\frac{2}{3}\pi
\displaystyle\int_{\alpha}^{\beta}
f(\theta)^3\sin\theta
~d\theta
\\\\
S
&=
2\pi
\displaystyle\int_{\alpha}^{\beta}
f(\theta)\sin\theta\sqrt{f(\theta)^2+f'(\theta)^2}
~d\theta
\end{align}
$$




コメント欄