こんにちはコーヤです。
このページでは、陰関数の極値を計算方法を勉強します。陽関数へ変形できない関数も偏微分を使うことで増減が分かるようになります。
陰関数の極値の計算方法
陰関数$f(x,y)=0$の極値を求めるとき、計算の方針は2つあります。
- 陽関数へ変形する
- 陰関数のまま計算する
パターン1の陽関数へ変形する方針なら、普通に微分して増減表を書けばOKです。この計算は高校生のときに習いました。
このページではパターン2の陰関数のまま極値の計算を行う方法を勉強します。
陰関数のまま計算をする方針は、陽関数のような増減表を書くのが難しくなります。なので増減表を使わずに極値を判定する条件を考えなければいけません。
では極値の条件はどのように表されるのか、慣れている陽関数へ変形するパターンの例を使用して考えてみます。
パターン1. 陽関数へ変形する
以下の陰関数の極値を計算します。
$$
x^3-3x-y=0
$$
これは$y$を移項することで
$$
y=x^3-3x
$$
と陽関数へ変形できます。この関数を2階微分して
$$
\begin{align}
y &= x^3-3x
\\\\
y’ &= 3x^2-3
\\\\
y'{}’ &= 6x
\end{align}
$$
この結果を利用して増減表とグラフを書くと
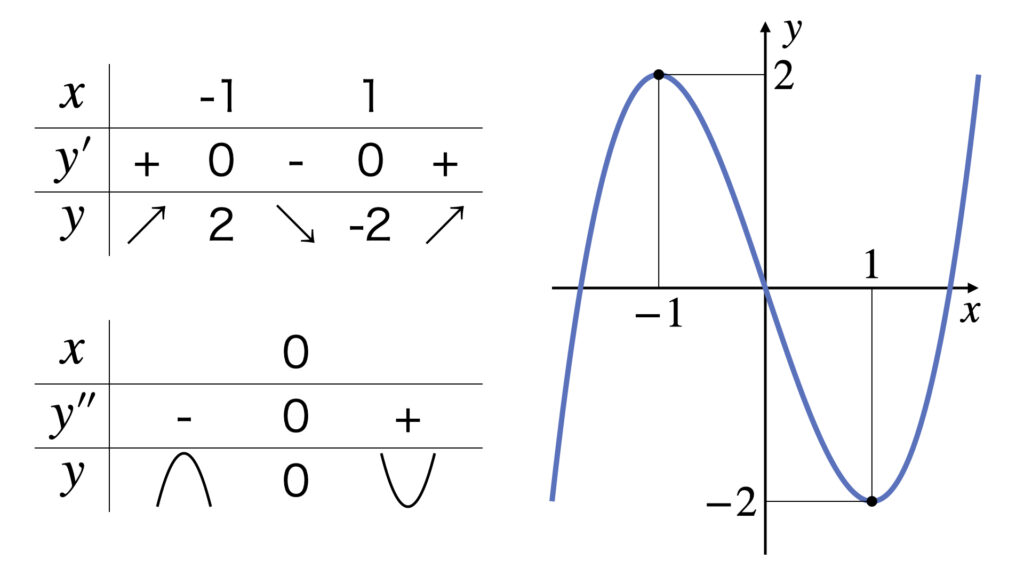
このようになるので、極値は$x=-1$のとき極大値、$x=1$のとき極小値と分かります。
さて、この例で注目したいのは計算過程ではなく極値の条件です。
極値は増加と減少が入れ替わる点ですので、$y’=0$になることが必要条件です。

$y’=0$は極値の必要条件であって十分条件ではありません。$y=x^3$のグラフを書くと$y’=0$でも極値にならないことが分かります。
極大値と極小値のどちらなのかは増減表の$y'{}’$の符号を使えば判断できます。$y'{}’$が正なら極小値、負なら極大値となります。
以上をまとめて極値の条件は以下のようになります。
- $y’=0$を満たす点が極値の候補である
- $y'{}’>0$なら極小値、$y'{}'<0$なら極大値である
陰関数の極値の条件の導出
陰関数にも極値の条件を当てはめるため、陽関数の$y’$と$y'{}’$に相当する関数を計算します。
陰関数を
$$
f(x,y)=0
$$
として、この両辺を$x$で微分すると
$$
\begin{align}
0
&=
\displaystyle\frac{d}{dx}f
\\\\&=
\displaystyle\frac{df}{dx}
\\\\&=
\displaystyle\frac{f_xdx+f_ydy}{dx}
\\\\&=
f_x+f_y\displaystyle\frac{dy}{dx}
\end{align}
$$
となります。途中の分子の式変形で全微分を使いました。
これより
$$
\displaystyle\frac{dy}{dx}
=
-\displaystyle\frac{f_x}{f_y}
$$
となります。左辺は$y$を$x$で微分した関数なので、陽関数の$y’$に相当する関数が導出できました。
さらにこの両辺を$x$で微分すると
$$
\begin{align}
\displaystyle\frac{d^2y}{dx^2}
&=
\displaystyle\frac{d}{dx}
\left(
-\displaystyle\frac{f_x}{f_y}
\right)
\\\\&=
-\displaystyle\frac
{
\left(
\displaystyle\frac{d}{dx}f_x
\right)
f_y
-f_x
\left(
\displaystyle\frac{d}{dx}f_y
\right)
}
{f_y^2}
\end{align}
$$
となります。式変形に分数関数の微分を使いました。
ここで
$$
\begin{align}
\displaystyle\frac{d}{dx}f_x
&=
\displaystyle\frac{df_x}{dx}
\\\\&=
\displaystyle\frac{f_{xx}dx+f_{xy}dy}{dx}
\\\\&=
f_{xx}+f_{xy}
\left(
\displaystyle\frac{dy}{dx}
\right)
\\\\&=
f_{xx}+f_{xy}
\left(
-\displaystyle\frac{f_x}{f_y}
\right)
\\\\&=
\displaystyle\frac{f_{xx}f_y-f_{xy}f_x}{f_y}
\end{align}
$$
$$
\begin{align}
\displaystyle\frac{d}{dx}f_y
&=
\displaystyle\frac{df_y}{dx}
\\\\&=
\displaystyle\frac{f_{yx}dx+f_{yy}dy}{dx}
\\\\&=
f_{yx}+f_{yy}
\left(
\displaystyle\frac{dy}{dx}
\right)
\\\\&=
f_{yx}+f_{yy}
\left(
-\displaystyle\frac{f_x}{f_y}
\right)
\\\\&=
\displaystyle\frac{f_{yx}f_y-f_{yy}f_x}{f_y}
\end{align}
$$
これらを代入して
$$
\begin{align}
\displaystyle\frac{d^2y}{dx^2}
&=
-\displaystyle\frac
{
\left(
\displaystyle\frac{d}{dx}f_x
\right)
f_y
-f_x
\left(
\displaystyle\frac{d}{dx}f_y
\right)
}
{f_y^2}
\\\\&=
-\displaystyle\frac
{
\left(
\displaystyle\frac{f_{xx}f_y-f_{xy}f_x}{f_y}
\right)
f_y
-f_x
\left(
\displaystyle\frac{f_{yx}f_y-f_{yy}f_x}{f_y}
\right)
}
{f_y^2}
\\\\&=
-\displaystyle\frac
{(f_{xx}f_y-f_{xy}f_x)f_y-f_x(f_{yx}f_y-f_{yy}f_x)}
{f_y^3}
\\\\&=
-\displaystyle\frac
{f_{xx}f_y^2-2f_{xy}f_xf_y+f_{yy}f_x^2}
{f_y^3}
\end{align}
$$
となります。左辺は$y$を$x$で2階微分した関数なので、陽関数の$y'{}’$に相当する関数が導出できました。
以上の結果を用いて極値の条件に当てはめます。
陽関数の極値の候補は$y’=0$を満たす点なので、陰関数の極値の候補は
$$
-\displaystyle\frac{f_x}{f_y}
=
0
$$
を満たす点となります。
分母が$0$だと定義できないので
$$
f_y
\neq
0
$$
も条件に加えないといけません。
この2つの条件が成り立つとき、2階微分した関数を整理すると
$$
\begin{align}
\displaystyle\frac{d^2y}{dx^2}
&=
-\displaystyle\frac
{f_{xx}f_y^2-2f_{xy}f_xf_y+f_{yy}f_x^2}
{f_y^3}
\\\\&=
-\displaystyle\frac{f_{xx}}{f_y}
-\displaystyle\frac{2f_{xy}}{f_y}
\left(
-\displaystyle\frac{f_x}{f_y}
\right)
-\displaystyle\frac{f_{yy}}{f_y}
\left(
-\displaystyle\frac{f_x}{f_y}
\right)^2
\\\\&=
-\displaystyle\frac{f_{xx}}{f_y}
-\displaystyle\frac{2f_{xy}}{f_y}
\cdot 0
-\displaystyle\frac{f_{yy}}{f_y}
\cdot 0^2
\\\\&=
-\displaystyle\frac{f_{xx}}{f_y}
\end{align}
$$
となるので、極大値と極小値の判断は
$$
-\displaystyle\frac{f_{xx}}{f_y}
<
0
$$
なら極大値の候補となり
$$
-\displaystyle\frac{f_{xx}}{f_y}
>
0
$$
なら極小値の候補となります。
残念ながら
$$
-\displaystyle\frac{f_{xx}}{f_y}
=
0
$$
のときは極大極小の判定はできません。陽関数に変形したり、グラフを書いたり、別の方法で判定しないといけません。
パターン2. 陰関数のまま計算する
それでは導出した条件を利用して、以下の陰関数の極値を計算します。(陰関数と言いつつ実際は単位円の式です。)
$$
f(x,y)=x^2+y^2-1=0
$$
まずは必要な偏導関数を計算します。
$$
\begin{align}
f_x(x,y) &= 2x
\\\\
f_y(x,y) &= 2y
\\\\
f_{xx}(x,y) &= 2
\end{align}
$$
極値の候補は
$$
\begin{align}
-\displaystyle\frac{f_x}{f_y} &= 0
\\\\
f_y &\neq 0
\end{align}
$$
この2つの条件を満たす点なので、計算すると$x=0$かつ$y\neq 0$となります。
ここで$x=0$のとき
$$
f(0,y)=y^2-1=0
$$
より$y=\pm 1$であることが分かります。
したがって、極値の候補は$(0,1)$と$(0,-1)$の2点です。
それぞれ極大極小を計算すると、点$(0,1)$について
$$
-\displaystyle\frac{f_{xx}}{f_y}
=
-\displaystyle\frac{2}{1}
<
0
$$
となるので極大値の候補です。
点$(0,-1)$について
$$
-\displaystyle\frac{f_{xx}}{f_y}
=
-\displaystyle\frac{2}{-1}
>
0
$$
となるので極大値の候補です。
$f(x,y)$は単位円の式ですので、$(0,1)$が極大値の候補、$(0,-1)$が極小値の候補となることは直感的な感覚とも一致します。
まとめ
陰関数の極値の候補は以下の条件を満たす点です。
$$
\begin{align}
-\displaystyle\frac{f_x}{f_y} &= 0
\\\\
f_y &\neq 0
\end{align}
$$
極値の候補において以下の関数が正なら極小値の候補、負なら極大値の候補です。
$$
-\displaystyle\frac{f_{xx}}{f_y}
$$




コメント欄