余因子展開の計算方法

こんにちはコーヤです。

このページでは余因子展開の計算方法を3ステップに分けて勉強します。余因子展開ができると高次の行列式が計算できるようになります。

余因子展開の3ステップ

余因子展開の計算は3ステップです。

余因子展開をすると$n$次の行列式が$n-1$次の行列式に変換されて求まります。$n$次から$n-1$次に変換し、$n-1$次から$n-2$次に変換し、どんどん小さくしていくことで3次か2次まで下げれば公式で求めることができます。

それでは以下の行列$X$を例に1ステップずつ見ていきましょう。

Step1. 展開する場所を決める

余因子展開する行or列を1個決めていきます。どこを選んでも計算結果は同じになるので、選ぶ基準は計算が楽かどうかです。

成分のどこかしらに0が含まれる行列なら、0がなるべく多くなるように行or列を選びましょう。0が多いほど余因子展開は楽になります。

例の行列$X$のように行列の各成分に値がある場合は、どこを選んでもさほど変わりません。

今回は1行目を選んで進めていきます。

Step2. 余因子を求める

選んだ行or列の余因子を求めていきます。

今回は1行目を選んだので、（1行1列）（1行2列）（1行3列）（1行4列）の4つの余因子を求めます。

1行1列の余因子=$X_{11}$
1行2列の余因子=$X_{12}$
1行3列の余因子=$X_{13}$
1行4列の余因子=$X_{14}$

とします。

Step3. 成分と余因子の積を足す

最後は行列の成分と対応する余因子の積を足していくだけです。

1行1列に注目します。1行1列の成分は$a$です。1行1列の余因子は$X_{11}$です。

1行1列で求めたい値は行列の成分と余因子の積なので、$aX_{11}$となります。

同様に1行2列は$bX_{12}$です。1行3列は$cX_{13}$です。1行4列は$dX_{14}$です。

これらの和が行列式になります。したがって

これで行列式が求まりました。

余因子展開の計算のイメージを画像にしました。画像で見ると展開してる感が伝わると思います。

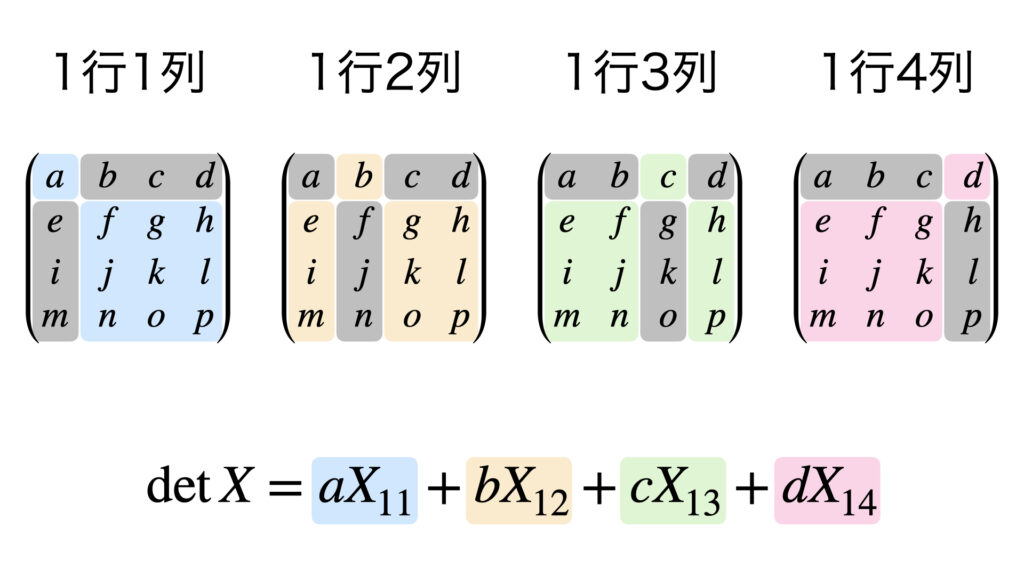
余因子展開の具体例

それでは具体例で余因子展開してみましょう。紙とペンがある方はぜひ手計算でやってみてください。

Step1. 展開する場所を決める

今回は1行目で余因子展開することにします。

Step2. 余因子を求める

1行1列の余因子=$A_{11}$
1行2列の余因子=$A_{12}$
1行3列の余因子=$A_{13}$
1行4列の余因子=$A_{14}$

とおくと

になります。

Step3. 成分と余因子の積を足す

行列式が求まりました。

この行列式を手計算で求めた方には伝わっていると思いますが、余因子展開は計算量が多くて大変です。

少しでも計算量を減らすためにはステップ1の場所決めで0が多い場所を選ぶことが重要です。

この行列を1行目で余因子展開すると、ステップ3の式が

こうなります。

つまりステップ2で$B_{12},B_{13},B_{14}$を計算する必要がなくなるんですね。

展開する場所に0があればある分だけステップ2の余因子の計算を省略できます。なるべく0が多い場所を選ぶのが余因子展開のコツです。

まとめ

余因子展開の計算は3ステップです。