こんにちはコーヤです。
このページでは3次の行列の対角化とジョルダン標準形の計算を全パターン勉強します。
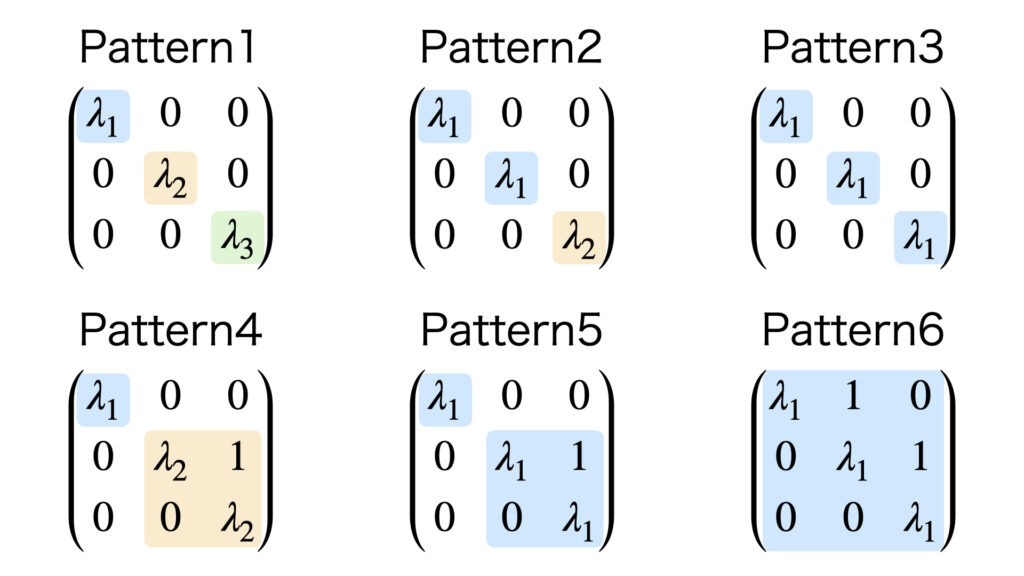
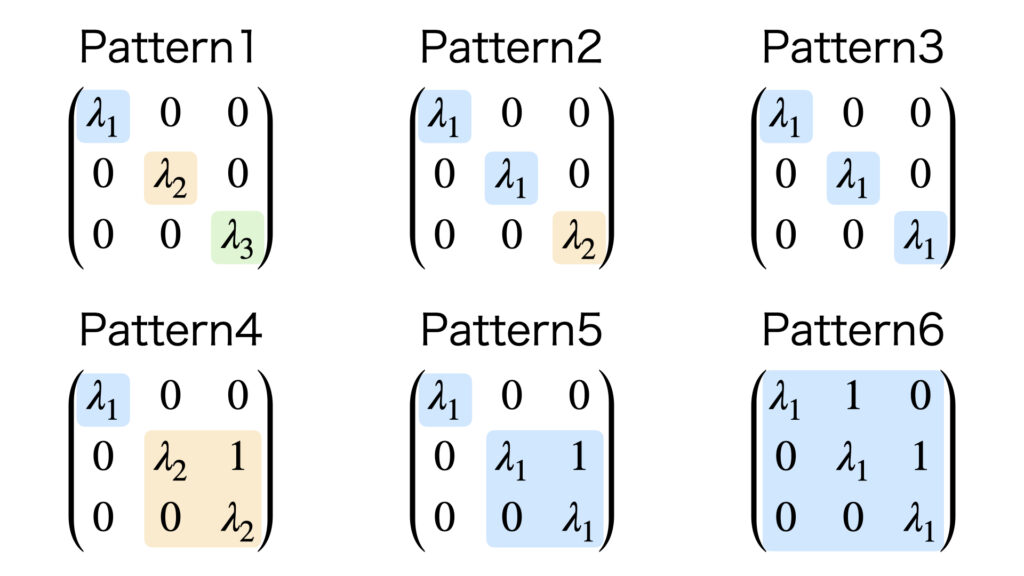
3次の対角化とジョルダン標準形の分類
3次の行列の対角化計算は以下の6パターンに分類することができます。
対角化の4ステップを再掲します。
- 固有値と固有ベクトルを求める
- 対角化可能か判定する
- 変換行列$P$を作る
- 逆行列$P^{-1}$を計算する
全てのパターンを計算できるよう勉強していきましょう。
パターン1
以下の行列Aを対角化します。
$$
A
=
\begin{pmatrix}
1 & 2 & 0 \\
-1 & -2 & 1 \\
0 & 0 & 1
\end{pmatrix}
$$
Step1. 固有値と固有ベクトルを求める
行列$A$の固有方程式は
$$
\begin{align}
\det (A-\lambda E)
&=
\begin{vmatrix}
1-\lambda & 2 & 0 \\
-1 & -2-\lambda & 1 \\
0 & 0 & 1-\lambda
\end{vmatrix}
\\\\&=
-(\lambda+1)\lambda(\lambda-1)
\end{align}
$$
これより固有値、固有ベクトルは
$$
\begin{array}{ccc}
\lambda_1=-1
&
\lambda_2=0
&
\lambda_3=1
\end{array}
$$
$$
\begin{array}{ccc}
\boldsymbol{v}_1
=
k_1
\begin{pmatrix}
1\\
-1\\
0
\end{pmatrix}
&
\boldsymbol{v}_2
=
k_2
\begin{pmatrix}
2\\
-1\\
0
\end{pmatrix}
&
\boldsymbol{v}_3
=
k_3
\begin{pmatrix}
1\\
0\\
1
\end{pmatrix}
\end{array}
$$
です。
Step2. 対角化可能か判定する
3次の行列$A$に対し線形独立な固有ベクトルが$\boldsymbol{v}_1, \boldsymbol{v}_2 , \boldsymbol{v}_3$の3個あるので、対角化可能です。
対角行列$D$は
$$
\begin{align}
D
&=
\begin{pmatrix}
\lambda_1 & 0 & 0 \\
0 & \lambda_2 & 0 \\
0 & 0 & \lambda_3
\end{pmatrix}
\\\\&=
\begin{pmatrix}
-1 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 1
\end{pmatrix}
\end{align}
$$
となります。
Step3. 変換行列$P$を作る
$k_1=k_2=k_3=1$として
$$
P
=
\begin{pmatrix}
1 & 2 & 1 \\
-1 & -1 & 0 \\
0 & 0 & 1
\end{pmatrix}
$$
とします。
Step4. 逆行列$P^{-1}$を計算する
$P$の逆行列を計算すると
$$
P^{-1}
=
\begin{pmatrix}
-1 & -2 & 1 \\
1 & 1 & -1 \\
0 & 0 & 1
\end{pmatrix}
$$
となります。
最終的に対角化の式$P^{-1}AP=D$に代入して
$$
\begin{pmatrix}
-1 & -2 & 1 \\
1 & 1 & -1 \\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 2 & 0 \\
-1 & -2 & 1 \\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 2 & 1 \\
-1 & -1 & 0 \\
0 & 0 & 1
\end{pmatrix}
=
\begin{pmatrix}
-1 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 1
\end{pmatrix}
$$
となり対角化完了です。
パターン2
以下の行列Aを対角化します。
$$
A
=
\begin{pmatrix}
1 & 2 & -2 \\
2 & 1 & -2 \\
2 & 2 & -3
\end{pmatrix}
$$
Step1. 固有値と固有ベクトルを求める
行列$A$の固有方程式は
$$
\begin{align}
\det (A-\lambda E)
&=
\begin{vmatrix}
1-\lambda & 2 & -2 \\
2 & 1-\lambda & -2 \\
2 & 2 & -3-\lambda
\end{vmatrix}
\\\\&=
-(\lambda+1)^2(\lambda-1)
\end{align}
$$
これより固有値、固有ベクトルは
$$
\begin{array}{cc}
\lambda_1=-1
&
\lambda_2=1
\end{array}
$$
$$
\begin{array}{cc}
\boldsymbol{v}_1
=
k_{11}
\begin{pmatrix}
1\\
0\\
1
\end{pmatrix}
+
k_{12}
\begin{pmatrix}
0\\
1\\
1
\end{pmatrix}
&
\boldsymbol{v}_2
=
k_2
\begin{pmatrix}
1\\
1\\
1
\end{pmatrix}
\end{array}
$$
です。
Step2. 対角化可能か判定する
3次の行列$A$に対し固有ベクトルが$\boldsymbol{v}_1, \boldsymbol{v}_2$の2個しかありませんので対角化不可能かと思いますが、ここで注意ポイントです。
$n$次の行列を対角化する条件は$n$個の「線形独立な」固有ベクトルがあることです。
固有ベクトルの式は2個しか得られませんでしたが、任意定数$k_{11},k_{12},k2$の値を調整して線形独立な固有ベクトルが3個になればOKです。
今回の例だと$\boldsymbol{v}_1$のうち$k_{11}=1,k_{12}=0$のときと$k_{11}=0,k_{12}=1$のときで線形独立な固有ベクトルが2個得られます。$\boldsymbol{v}_2$も合わせて線形独立な固有ベクトルが3個になるので、対角化可能です。
対角行列$D$は
$$
\begin{align}
D
&=
\begin{pmatrix}
\lambda_1 & 0 & 0 \\
0 & \lambda_1 & 0 \\
0 & 0 & \lambda_2
\end{pmatrix}
\\\\&=
\begin{pmatrix}
-1 & 0 & 0 \\
0 & -1 & 0 \\
0 & 0 & 1
\end{pmatrix}
\end{align}
$$
となります。
Step3. 変換行列$P$を作る
変換行列$P$は線形独立な固有ベクトルを並べて作ったものです。
- 1列目は$\boldsymbol{v}_1$の$k_{11}=1,k_{12}=0$の場合の固有ベクトル
- 2列目は$\boldsymbol{v}_1$の$k_{11}=0,k_{12}=1$の場合の固有ベクトル
- 3列目は$\boldsymbol{v}_2$の$k_2=1$の場合の固有ベクトル
以上のように任意定数を設定して
$$
P
=
\begin{pmatrix}
1 & 0 & 1 \\
0 & 1 & 1 \\
1 & 1 & 1
\end{pmatrix}
$$
とします。
Step4. 逆行列$P^{-1}$を計算する
$P$の逆行列を計算すると
$$
P^{-1}
=
\begin{pmatrix}
0 & -1 & 1 \\
-1 & 0 & 1 \\
1 & 1 & -1
\end{pmatrix}
$$
となります。
最終的に対角化の式$P^{-1}AP=D$に代入して
$$
\begin{pmatrix}
0 & -1 & 1 \\
-1 & 0 & 1 \\
1 & 1 & -1
\end{pmatrix}
\begin{pmatrix}
1 & 2 & -2 \\
2 & 1 & -2 \\
2 & 2 & -3
\end{pmatrix}
\begin{pmatrix}
1 & 0 & 1 \\
0 & 1 & 1 \\
1 & 1 & 1
\end{pmatrix}
=
\begin{pmatrix}
-1 & 0 & 0 \\
0 & -1 & 0 \\
0 & 0 & 1
\end{pmatrix}
$$
となり対角化完了です。
パターン3
残念ながらパターン3は存在しません。
存在しないことは簡単に確認できるので確認してみましょう。
行列$A$を対角化してパターン3になると仮定します。
パターン3の対角行列$D$は以下のように変形できます。
$$
\begin{align}
D
&=
\begin{pmatrix}
\lambda_1 & 0 & 0 \\
0 & \lambda_1 & 0 \\
0 & 0 & \lambda_1
\end{pmatrix}
\\\\&=
\lambda_1 E
\end{align}
$$
これを対角化の式$P^{-1}AP=D$に代入して
$$
P^{-1}AP = \lambda_1 E
$$
両辺に左側から$P$をかけて
$$
\begin{align}
AP
&=
P \lambda_1 E
\\\\&=
\lambda_1 P
\end{align}
$$
両辺に右側から$P^{-1}$をかけて
$$
\begin{align}
A
&=
\lambda_1 P P^{-1}
\\\\&=
\lambda_1 E
\\\\&=
D
\end{align}
$$
これより$A=D$であればパターン3になることが分かります。
対角化する前の行列$A$が$A=D$ということは既に対角行列になっています。対角行列を対角化計算する必要はありませんので、パターン3は存在しないということになります。
パターン4
以下の行列Aを対角化します。
$$
A
=
\begin{pmatrix}
1 & 0 & -1 \\
1 & -2 & 1 \\
1 & -1 & 0
\end{pmatrix}
$$
Step1. 固有値と固有ベクトルを求める
行列$A$の固有方程式は
$$
\begin{align}
\det (A-\lambda E)
&=
\begin{vmatrix}
1-\lambda & 0 & -1 \\
1 & -2-\lambda & 1 \\
1 & -1 & -\lambda
\end{vmatrix}
\\\\&=
-(\lambda+1)\lambda^2
\end{align}
$$
これより固有値、固有ベクトルは
$$
\begin{array}{cc}
\lambda_1=-1
&
\lambda_2=0
\end{array}
$$
$$
\begin{array}{cc}
\boldsymbol{v}_1
=
k_1
\begin{pmatrix}
1\\
3\\
2
\end{pmatrix}
&
\boldsymbol{v}_2
=
k_2
\begin{pmatrix}
1\\
1\\
1
\end{pmatrix}
\end{array}
$$
です。
Step2. 対角化可能か判定する
3次の行列$A$に対し固有ベクトルが$\boldsymbol{v}_1, \boldsymbol{v}_2$の2個しかありません。任意定数の値を調整しても、線形独立な固有ベクトルは2個しか得られません。
よって対角化不可能のためジョルダン標準形を目指します。
ジョルダン標準形$J$は
$$
\begin{align}
J
&=
\begin{pmatrix}
\lambda_1 & 0 & 0 \\
0 & \lambda_2 & 1 \\
0 & 0 & \lambda_2
\end{pmatrix}
\\\\&=
\begin{pmatrix}
-1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 0 & 0
\end{pmatrix}
\end{align}
$$
となります。
Step3. 変換行列$P$を作る
広義固有ベクトル$\boldsymbol{v}’_2$は以下のジョルダン鎖の条件を満たします。
$$
(A-\lambda E) \boldsymbol{v}’_2 = \boldsymbol{v}_2
$$
この非同次連立1次方程式の拡大係数行列は以下のようになります。
$$
\left(
\begin{array}{ccc|c}
1 & 0 & -1 & k_2 \\
1 & -2 & 1 & k_2 \\
1 & -1 & 0 & k_2 \\
\end{array}
\right)
$$
これは自由度1なので任意定数1個で$\boldsymbol{v}’_2$を表現できます。
任意定数を$k’_2$として
$$
\boldsymbol{v}’_2
=
k_2
\begin{pmatrix}
1 \\
0 \\
0
\end{pmatrix}
+
k’_2
\begin{pmatrix}
1 \\
1 \\
1
\end{pmatrix}
$$
となります。
それでは変換行列$P$を作ります。
- 1列目は$\boldsymbol{v}_1$の$k_1=1$の場合の固有ベクトル
- 2列目は$\boldsymbol{v}_2$の$k_2=1$の場合の固有ベクトル
- 3列目は$\boldsymbol{v}’_2$の$k_2=1,k’_2=0$の場合の広義固有ベクトル
2列目と3列目は鎖でつながっているので、共通している任意定数は同じ値を使わないといけません。
以上のように任意定数を設定して
$$
P
=
\begin{pmatrix}
1 & 1 & 1 \\
3 & 1 & 0 \\
2 & 1 & 0
\end{pmatrix}
$$
とします。
Step4. 逆行列$P^{-1}$を計算する
$P$の逆行列を計算すると
$$
P^{-1}
=
\begin{pmatrix}
0 & 1 & -1 \\
0 & -2 & 3 \\
1 & 1 & -2
\end{pmatrix}
$$
となります。
最終的に対角化の式$P^{-1}AP=J$に代入して
$$
\begin{pmatrix}
0 & 1 & -1 \\
0 & -2 & 3 \\
1 & 1 & -2
\end{pmatrix}
\begin{pmatrix}
1 & 0 & -1 \\
1 & -2 & 1 \\
1 & -1 & 0
\end{pmatrix}
\begin{pmatrix}
1 & 1 & 1 \\
3 & 1 & 0 \\
2 & 1 & 0
\end{pmatrix}
=
\begin{pmatrix}
-1 & 0 & 0 \\
0 & 0 & 1 \\
0 & 0 & 0
\end{pmatrix}
$$
となり対角化完了です。
パターン5
以下の行列Aを対角化します。
$$
A
=
\begin{pmatrix}
3 & 3 & 1 \\
-1 & -1 & -1 \\
2 & 6 & 4
\end{pmatrix}
$$
Step1. 固有値と固有ベクトルを求める
行列$A$の固有方程式は
$$
\begin{align}
\det (A-\lambda E)
&=
\begin{vmatrix}
3-\lambda & 3 & 1 \\
-1 & -1-\lambda & -1 \\
2 & 6 & 4-\lambda
\end{vmatrix}
\\\\&=
-(\lambda-2)^3
\end{align}
$$
これより固有値、固有ベクトルは
$$
\lambda_1=2
$$
$$
\boldsymbol{v}_1
=
k_{11}
\begin{pmatrix}
3\\
-1\\
0
\end{pmatrix}
+
k_{12}
\begin{pmatrix}
1\\
0\\
-1
\end{pmatrix}
$$
です。
Step2. 対角化可能か判定する
3次の行列$A$に対し固有ベクトルが$\boldsymbol{v}_1$の1個しかありません。任意定数の値を調整しても、線形独立な固有ベクトルは2個しか得られません。
よって対角化不可能のためジョルダン標準形を目指します。
ジョルダン標準形$J$は
$$
\begin{align}
J
&=
\begin{pmatrix}
\lambda_1 & 0 & 0 \\
0 & \lambda_1 & 1 \\
0 & 0 & \lambda_1
\end{pmatrix}
\\\\&=
\begin{pmatrix}
2 & 0 & 0 \\
0 & 2 & 1 \\
0 & 0 & 2
\end{pmatrix}
\end{align}
$$
となります。
Step3. 変換行列$P$を作る
広義固有ベクトル$\boldsymbol{v}’_1$は以下のジョルダン鎖の条件を満たします。
$$
(A-\lambda E) \boldsymbol{v}’_1 = \boldsymbol{v}_1
$$
この非同次連立1次方程式の拡大係数行列は以下のようになります。
$$
\left(
\begin{array}{ccc|c}
1 & 3 & 1 & 3k_{11}+k_{12} \\
-1 & -3 & -1 & -k_{11} \\
2 & 6 & 2 & -k_{12}
\end{array}
\right)
$$
これを階段行列に変形すると
$$
\left(
\begin{array}{ccc|c}
1 & 3 & 1 & 3k_{11}+k_{12} \\
0 & 0 & 0 & 2k_{11}+k_{12} \\
0 & 0 & 0 & -6k_{11}-3k_{12}
\end{array}
\right)
$$
広義固有ベクトルが存在するためにはこの非同次連立1次方程式が解を持たなければいけません。
つまり
$$
\begin{cases}
2k_{11}+k_{12}=0 \\
-6k_{11}-3k_{12}=0
\end{cases}
$$
この条件を満たさないと係数行列と拡大係数行列のランクが合わずに解なしとなってしまいます。
この条件式2つを満たすように
$$
k_{12}=-2k_{11}
$$
とします。これを満たすような固有ベクトルを用いることで広義固有ベクトルが存在するようになります。
拡大係数行列にこの条件を代入して書き直すと
$$
\left(
\begin{array}{ccc|c}
1 & 3 & 1 & 3k_{11}+k_{12} \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0
\end{array}
\right)
$$
これは自由度2なので任意定数2個で$\boldsymbol{v}’_1$を表現できます。
任意定数を$k’_{11},k’_{12}$として
$$
\boldsymbol{v}’_1
=
k_{11}
\begin{pmatrix}
3 \\
0 \\
0
\end{pmatrix}
+
k_{12}
\begin{pmatrix}
1 \\
0 \\
0
\end{pmatrix}
+
k’_{11}
\begin{pmatrix}
3 \\
-1 \\
0
\end{pmatrix}
+
k’_{12}
\begin{pmatrix}
1 \\
0 \\
-1
\end{pmatrix}
$$
となります。
それでは変換行列$P$を作ります。
ジョルダン鎖の条件を満たすように任意定数の値を設定します。
広義固有ベクトルが存在するために固有ベクトルが満たすべき条件、という流れで非同次連立1次方程式を解きました。つまり$k_{12}=-2k_{11}$を満たすべきは広義固有ベクトルではなく固有ベクトルです。
今回は$k_{11}=1,k_{12}=-2$として固有ベクトルを作ります。
変換行列$P$を1列目と2列目が固有ベクトル、3列目が広義固有ベクトルの形で作るとします。
固有ベクトルと広義固有ベクトルの間の鎖なので、2列目と3列目の鎖となります。なので2列目の固有ベクトルを$k_{11}=1,k_{12}=-2$とします。
逆に1列目は$k_{12}=-2k_{11}$を満たしてはいけません。変換行列$P$は線形独立なベクトルを並べたものなので、2列目と線形独立になるように1列目の固有ベクトルを決めます。
これらの条件を満たすように
- 1列目は$\boldsymbol{v}_1$の$k_{11}=0,k_{12}=1$の場合の固有ベクトル
- 2列目は$\boldsymbol{v}_1$の$k_{11}=1,k_{12}=-2$の場合の固有ベクトル
- 3列目は$\boldsymbol{v}’_1$の$k_{11}=1,k_{12}=-2,k’_{11}=0,k’_{12}=0$の場合の広義固有ベクトル
2列目と3列目は鎖でつながっているので、共通している任意定数は同じ値を使わないといけません。
以上のように任意定数を設定して
$$
P
=
\begin{pmatrix}
1 & 1 & 1 \\
0 & -1 & 0 \\
-1 & 2 & 0
\end{pmatrix}
$$
とします。
Step4. 逆行列$P^{-1}$を計算する
$P$の逆行列を計算すると
$$
P^{-1}
=
\begin{pmatrix}
0 & -2 & -1 \\
0 & -1 & 0 \\
1 & 3 & 1
\end{pmatrix}
$$
となります。
最終的に対角化の式$P^{-1}AP=J$に代入して
$$
\begin{pmatrix}
0 & -2 & -1 \\
0 & -1 & 0 \\
1 & 3 & 1
\end{pmatrix}
\begin{pmatrix}
3 & 3 & 1 \\
-1 & -1 & -1 \\
2 & 6 & 4
\end{pmatrix}
\begin{pmatrix}
1 & 1 & 1 \\
0 & -1 & 0 \\
-1 & 2 & 0
\end{pmatrix}
=
\begin{pmatrix}
2 & 0 & 0 \\
0 & 2 & 1 \\
0 & 0 & 2
\end{pmatrix}
$$
となり対角化完了です。
パターン6
以下の行列Aを対角化します。
$$
A
=
\begin{pmatrix}
-2 & -1 & -1 \\
-1 & -3 & -2 \\
0 & 1 & -1
\end{pmatrix}
$$
Step1. 固有値と固有ベクトルを求める
行列$A$の固有方程式は
$$
\begin{align}
\det (A-\lambda E)
&=
\begin{vmatrix}
-2-\lambda & -1 & -1 \\
-1 & -3-\lambda & -2 \\
0 & 1 & -1-\lambda
\end{vmatrix}
\\\\&=
-(\lambda+2)^3
\end{align}
$$
これより固有値、固有ベクトルは
$$
\lambda_1=-2
$$
$$
\boldsymbol{v}_1
=
k_1
\begin{pmatrix}
1\\
1\\
-1
\end{pmatrix}
$$
です。
Step2. 対角化可能か判定する
3次の行列$A$に対し固有ベクトルが$\boldsymbol{v}_1$の1個しかありません。任意定数の値を調整しても、線形独立な固有ベクトルは1個しか得られません。
よって対角化不可能のためジョルダン標準形を目指します。
ジョルダン標準形$J$は
$$
\begin{align}
J
&=
\begin{pmatrix}
\lambda_1 & 1 & 0 \\
0 & \lambda_1 & 1 \\
0 & 0 & \lambda_1
\end{pmatrix}
\\\\&=
\begin{pmatrix}
-2 & 1 & 0 \\
0 & -2 & 1 \\
0 & 0 & -2
\end{pmatrix}
\end{align}
$$
となります。
Step3. 変換行列$P$を作る
広義固有ベクトル$\boldsymbol{v}’_1$は以下のジョルダン鎖の条件を満たします。
$$
(A-\lambda E) \boldsymbol{v}’_1 = \boldsymbol{v}_1
$$
この非同次連立1次方程式の拡大係数行列は以下のようになります。
$$
\left(
\begin{array}{ccc|c}
0 & -1 & -1 & k_1 \\
-1 & -1 & -2 & k_1 \\
0 & 1 & 1 & -k_1
\end{array}
\right)
$$
これを階段行列に変形すると
$$
\left(
\begin{array}{ccc|c}
1 & 0 & 1 & 0 \\
0 & 1 & 1 & -k_1 \\
0 & 0 & 0 & 0
\end{array}
\right)
$$
これは自由度1なので任意定数1個で$\boldsymbol{v}’_1$を表現できます。
任意定数を$k’_1$として
$$
\boldsymbol{v}’_1
=
k_1
\begin{pmatrix}
0 \\
-1 \\
0
\end{pmatrix}
+
k’_1
\begin{pmatrix}
1 \\
1 \\
-1
\end{pmatrix}
$$
となります。
現時点で固有ベクトル1個、広義固有ベクトル1個の計2個なので対角化計算のためにはもう1個広義固有ベクトルが必要です。
広義固有ベクトル$\boldsymbol{v}'{}’_1$は以下のジョルダン鎖の条件を満たします。
$$
(A-\lambda E) \boldsymbol{v}'{}’_1 = \boldsymbol{v}’_1
$$
この非同次連立1次方程式の拡大係数行列は以下のようになります。
$$
\left(
\begin{array}{ccc|c}
0 & -1 & -1 & k’_1 \\
-1 & -1 & -2 & -k_1+k’_1 \\
0 & 1 & 1 & -k’_1
\end{array}
\right)
$$
これを階段行列に変形すると
$$
\left(
\begin{array}{ccc|c}
1 & 0 & 1 & k_1 \\
0 & 1 & 1 & -k’_1 \\
0 & 0 & 0 & 0
\end{array}
\right)
$$
これは自由度1なので任意定数1個で$\boldsymbol{v}'{}’_1$を表現できます。
任意定数を$k'{}’_1$として
$$
\boldsymbol{v}'{}’_1
=
k_1
\begin{pmatrix}
1 \\
0 \\
0
\end{pmatrix}
+
k’_1
\begin{pmatrix}
0 \\
-1 \\
0
\end{pmatrix}
+
k'{}’_1
\begin{pmatrix}
1 \\
1 \\
-1
\end{pmatrix}
$$
となります。
それでは変換行列$P$を作ります。
- 1列目は$\boldsymbol{v}_1$の$k_1=1$の場合の固有ベクトル
- 2列目は$\boldsymbol{v}’_1$の$k_1=1,k’_1=0$の場合の広義固有ベクトル
- 3列目は$\boldsymbol{v}'{}’_1$の$k_1=1,k’_1=0,k'{}’_1=0$の場合の広義固有ベクトル
1列目と2列目は鎖でつながっているので、共通している任意定数は同じ値を使わないといけません。
2列目と3列目は鎖でつながっているので、共通している任意定数は同じ値を使わないといけません。
以上のように任意定数を設定して
$$
P
=
\begin{pmatrix}
1 & 0 & 1 \\
1 & -1 & 0 \\
-1 & 0 & 0
\end{pmatrix}
$$
とします。
Step4. 逆行列$P^{-1}$を計算する
$P$の逆行列を計算すると
$$
P^{-1}
=
\begin{pmatrix}
0 & 0 & -1 \\
0 & -1 & -1 \\
1 & 0 & 1
\end{pmatrix}
$$
となります。
最終的に対角化の式$P^{-1}AP=J$に代入して
$$
\begin{pmatrix}
0 & 0 & -1 \\
0 & -1 & -1 \\
1 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
-2 & -1 & -1 \\
-1 & -3 & -2 \\
0 & 1 & -1
\end{pmatrix}
\begin{pmatrix}
1 & 0 & 1 \\
1 & -1 & 0 \\
-1 & 0 & 0
\end{pmatrix}
=
\begin{pmatrix}
-2 & 1 & 0 \\
0 & -2 & 1 \\
0 & 0 & -2
\end{pmatrix}
$$
となり対角化完了です。
まとめ
3次の対角化、ジョルダン標準形は6パターンのどれかに分類できます。




コメント欄