こんにちはコーヤです。
このページでは内積空間と直交補空間の性質を勉強します。線形空間に演算を定義を追加します。
内積空間の条件
線形空間には和の演算とスカラー倍の演算が定義されていました。
もう1つ演算を追加して、内積の演算を定義したのが内積空間です。いわば線形空間の進化系です。
内積の演算が満たすべき性質は4つあります。それでは1つずつ見ていきましょう。
線形空間$V$の任意の元$\boldsymbol{a} , \boldsymbol{b} , \boldsymbol{c}$とし、任意のスカラーを$k$とします。
Filter1
交換法則を満たすか調べます。
$$
\boldsymbol{a} \cdot \boldsymbol{b}
=
\boldsymbol{b} \cdot \boldsymbol{a}
$$
が成り立てばOKです。
Filter2
和の分配法則を満たすか調べます。
$$
(\boldsymbol{a} + \boldsymbol{b} ) \cdot \boldsymbol{c}
=
\boldsymbol{a} \cdot \boldsymbol{c} + \boldsymbol{b} \cdot \boldsymbol{c}
$$
$$
\boldsymbol{a} \cdot ( \boldsymbol{b} + \boldsymbol{c} )
=
\boldsymbol{a} \cdot \boldsymbol{b} + \boldsymbol{a} \cdot \boldsymbol{c}
$$
が成り立てばOKです。
Filter3
スカラー倍の分配法則を満たすか調べます。
$$
( k \boldsymbol{a} ) \cdot \boldsymbol{b}
=
k ( \boldsymbol{a} \cdot \boldsymbol{b} )
$$
$$
\boldsymbol{a} \cdot ( k \boldsymbol{b} )
=
k ( \boldsymbol{a} \cdot \boldsymbol{b} )
$$
が成り立てばOKです。
Filter4
自身との内積を調べます。
$$
\boldsymbol{a} \cdot \boldsymbol{a}
\geq
0
$$
が成り立てばOKです。
線形空間$V$がこれら4つのフィルターを突破したら内積空間になります。
線形空間はベクトルとか関数とか色々なものが該当しました。内積はベクトルの計算だから内積空間になるのはベクトルだけかと思いますが、関数も内積を定義できます。
関数$f(x)$と$g(x)$の内積を
$$
f(x) \cdot g(x)
=
\int_{-\pi}^{\pi} f(x)g(x) ~dx
$$
と定義すると、上記4つの性質を満たします。
内積と言われるとどうしてもベクトルをイメージしてしまうので、関数の内積と言われてもイメージが湧きませんが、関数を無理やりベクトルっぽく表すとこんな感じです。
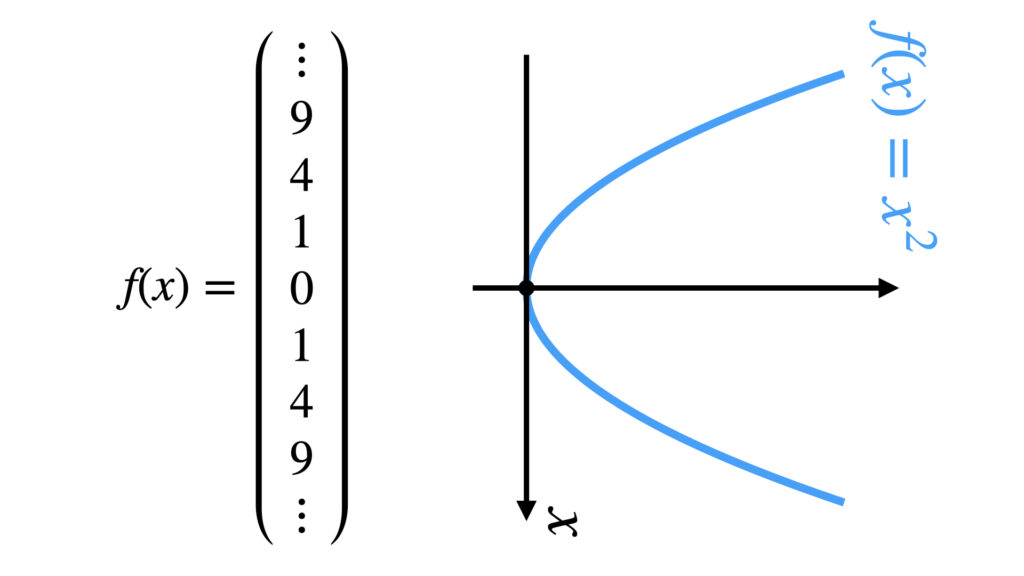
「内積はベクトルの演算」のイメージは払拭しましょう。
ノルムの性質
内積空間$V$の元$\boldsymbol{a}$のノルムを以下のように定義します。
$$
\| \boldsymbol{a} \|
=
\sqrt{\boldsymbol{a} \cdot \boldsymbol{a}}
$$
ベクトルの長さみたいな値のことを一般化して、ノルムと呼びます。
ノルムは以下の4つの性質を満たします。内積空間$V$の任意の元$\boldsymbol{a} , \boldsymbol{b} $とし、任意のスカラーを$k$とします。
$$
\begin{array}{cl}
(1) & \| \boldsymbol{a} \| \geq 0 \\
(2) & \| k\boldsymbol{a} \| = |k| \| \boldsymbol{a} \| \\
(3) & | \boldsymbol{a} \cdot \boldsymbol{b} | \leq \| \boldsymbol{a} \|\| \boldsymbol{b} \| \\
(4) & \| \boldsymbol{a} + \boldsymbol{b} \| \leq \| \boldsymbol{a} \| + \| \boldsymbol{b} \|
\end{array}
$$
縦線ばっかりで見にくいですが、ベクトルをイメージしながら式を1つ1つ見ていけば納得できる性質だと思います。
角度の性質
内積とノルムを使うと角度も定義できるようになります。「なす角」と呼ばれる角度です。
$\boldsymbol{a}$と$\boldsymbol{b}$のなす角$\theta$を以下のように定義します。
$$
\left.
\begin{array}{cc}
\cos \theta
=
\displaystyle \frac
{\boldsymbol{a} \cdot \boldsymbol{b}}
{\| \boldsymbol{a} \| \| \boldsymbol{b} \|}
&
( 0 \leq \theta \leq \pi )
\end{array}
\right.
$$
続いて直交の定義もします。
$$
\begin{array}{ccc}
\boldsymbol{a} \perp \boldsymbol{b}
&
\Leftrightarrow
&
\boldsymbol{a} \cdot \boldsymbol{b}=0
\end{array}
$$
このように内積が0の場合を直交と定義します。
$\cos \theta =0$の場合だけが直交となるわけではなく、$\boldsymbol{a}$か$\boldsymbol{b}$が零ベクトルの場合も直交になります。
直交補空間の具体例
直交が定義されたことによって、新たな部分空間である直交補空間というのが登場します。
直交補空間は部分空間と直和の続編のような空間です。部分空間や直和が不安な方はご覧ください。
内積空間$V$の部分空間を$W$とし、$W$に直交する$V$の元を集めて作る空間を直交補空間$W^{\perp}$といいます。
言葉で見ても難しいのでさっそく具体例を見ていきます。
具体例1
内積空間$V$を2次元列ベクトル空間$R^2$とします。
$V$の元$\boldsymbol{f}_1$が作る部分空間$W$を$y=2x$の直線とします。
この部分空間に直交する$V$の元を集めてきます。
$$
\left.
\begin{array}{ccc}
\boldsymbol{f}_1
=
\begin{pmatrix}
1 \\
2
\end{pmatrix}
&
\boldsymbol{f}_2
=
\begin{pmatrix}
2 \\
-1
\end{pmatrix}
&
\boldsymbol{f}_3
=
\begin{pmatrix}
-4 \\
2
\end{pmatrix}
\end{array}
\right.
$$
例えば$\boldsymbol{f}_2$と$\boldsymbol{f}_3$が集まったとします。$\boldsymbol{f}_2$と$\boldsymbol{f}_3$が$W$と直交することを確認します。
$W$は$y=2x$の直線なので、$W$上の点は$(t,2t)$と表せます。この点$(t,2t)$を表すベクトルを$\boldsymbol{w}$として
$$
\boldsymbol{w} \cdot \boldsymbol{f}_2
=
\begin{pmatrix}
t \\
2t
\end{pmatrix}
\cdot
\begin{pmatrix}
2 \\
-1
\end{pmatrix}
=0
$$
$$
\boldsymbol{w} \cdot \boldsymbol{f}_3
=
\begin{pmatrix}
t \\
2t
\end{pmatrix}
\cdot
\begin{pmatrix}
-4 \\
2
\end{pmatrix}
=0
$$
どちらも内積が0になるため直交の条件を満たしています。
$W$に直交する元$\boldsymbol{f}_2 , \boldsymbol{f}_3$が作る部分空間が直交補空間$W^{\perp}$です。つまり
$$
\begin{align}
c_1 \boldsymbol{f}_2 + c_2 \boldsymbol{f}_3
&=
c_1
\begin{pmatrix}
2 \\
-1
\end{pmatrix}
+
c_2
\begin{pmatrix}
-4 \\
2
\end{pmatrix}
\\\\&=
\begin{pmatrix}
2c_1-4c_2 \\
-c_1+2c_2
\end{pmatrix}
\end{align}
$$
これより$W^{\perp}$は$x+2y=0$の直線だと分かります。
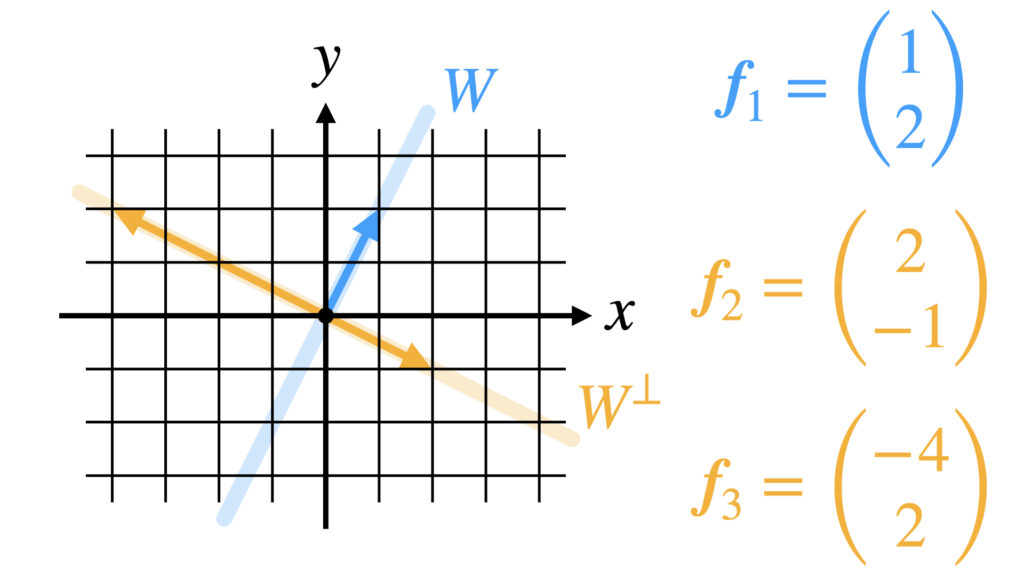
具体例2
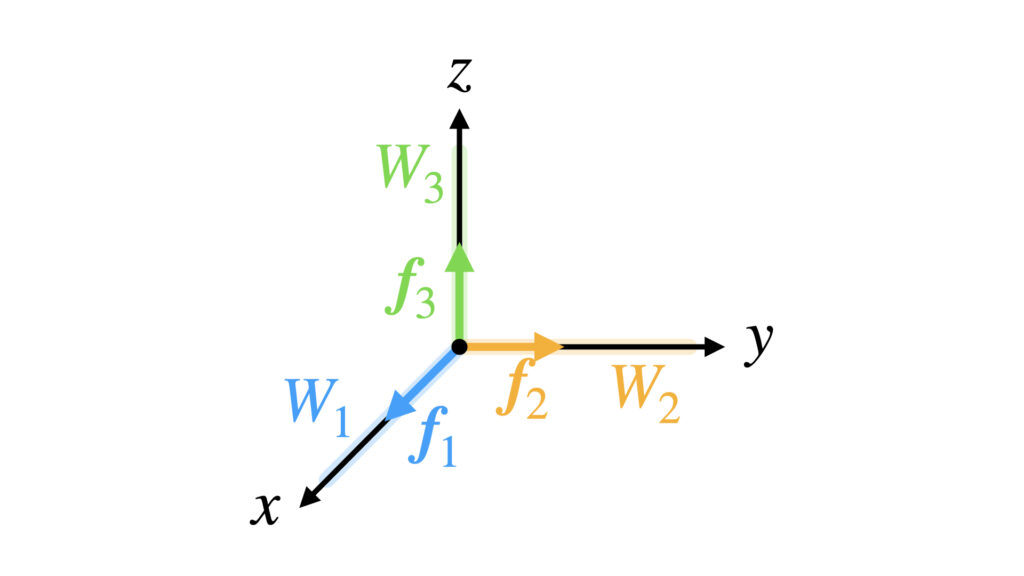
内積空間$V$を3次元列ベクトル空間$R^3$とします。
$V$の元$\boldsymbol{f}_1$が作る部分空間$W_1$を$y=z=0$の直線とします。
この部分空間に直交する$V$の元を集めてきます。
$$
\left.
\begin{array}{ccc}
\boldsymbol{f}_1
=
\begin{pmatrix}
1 \\
0 \\
0
\end{pmatrix}
&
\boldsymbol{f}_2
=
\begin{pmatrix}
0 \\
1 \\
0
\end{pmatrix}
&
\boldsymbol{f}_3
=
\begin{pmatrix}
0 \\
0 \\
1
\end{pmatrix}
\end{array}
\right.
$$
今回も$\boldsymbol{f}_2$と$\boldsymbol{f}_3$が集まったとします。$\boldsymbol{f}_1 \perp \boldsymbol{f}_2$かつ$\boldsymbol{f}_1 \perp \boldsymbol{f}_3$です。
$\boldsymbol{f}_2$が作る部分空間を$W_2$、$\boldsymbol{f}_3$が作る部分空間を$W_3$とします。
これを見ると$W_1$の直交補空間は$W_2$と$W_3$の2つのように見えますが、ミスしやすい注意ポイントです。
$W_1$の直交補空間は$W_1$に直交する元を集めて作る空間なので、$\boldsymbol{f}_2$と$\boldsymbol{f}_3$が作る部分空間です。
$W_2$と$W_3$は$\boldsymbol{f}_2$と$\boldsymbol{f}_3$それぞれが作る部分空間なので直交補空間にはなりません。
$\boldsymbol{f}_2$と$\boldsymbol{f}_3$が作る空間は$\boldsymbol{f}_2$と$\boldsymbol{f}_3$の線形結合で表せるので
$$
\begin{align}
c_1 \boldsymbol{f}_2 + c_2 \boldsymbol{f}_3
&=
c_1
\begin{pmatrix}
0 \\
1 \\
0
\end{pmatrix}
+
c_2
\begin{pmatrix}
0 \\
0 \\
1
\end{pmatrix}
\\\\&=
\begin{pmatrix}
0 \\
c_1 \\
c_2
\end{pmatrix}
\end{align}
$$
これより$W^{\perp}$は$x=0$の平面です。
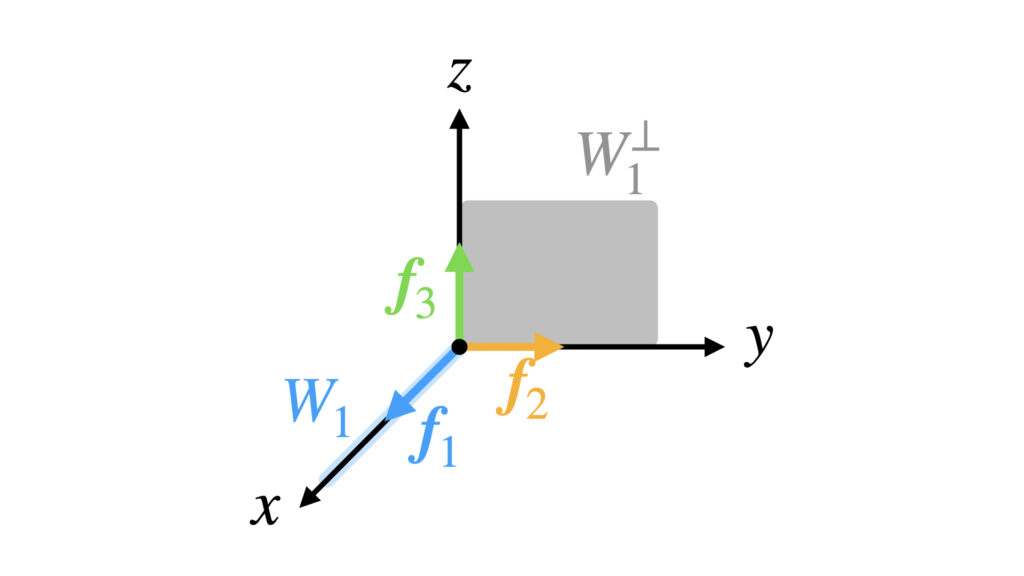
直交補空間の検算
具体例2で見たように、部分空間$W$に直交する元を全て集めないと直交補空間$W^{\perp}$は作れません。
$W$に直交する元の探し漏れがないかどうか、以下の公式で確認できます。
$$
V=W \oplus W^{\perp}
$$
直交補空間$W^{\perp}$を求めたら、この公式が成り立っているかで確認すれば大丈夫です。
まとめ
内積空間は線形空間の性質と内積の性質4つを満たす集合です。
直交補空間は部分空間に直交する元が作る部分空間です。






コメント欄