こんにちはコーヤです。
このページでは線形代数の定番問題である行列の対角化を4ステップに分けて勉強します。
対角化の計算の流れ
まずは対角化の計算の流れから見ていきます。具体的な計算はページ後半でやります。
2次の行列$A$とその固有値$\lambda_1,\lambda_2$と固有ベクトル$\boldsymbol{v}_1, \boldsymbol{v}_2$を例にします。
固有値、固有ベクトルは以下の式を満たすものでした。
$$
\begin{align}
A \boldsymbol{v}_1 &= \lambda_1 \boldsymbol{v}_1
\\\\
A \boldsymbol{v}_2 &= \lambda_2 \boldsymbol{v}_2
\end{align}
$$
これを行列の形で表現すると
$$
A
\begin{pmatrix}
\boldsymbol{v}_1 & \boldsymbol{v}_2
\end{pmatrix}
=
\begin{pmatrix}
\boldsymbol{v}_1 & \boldsymbol{v}_2
\end{pmatrix}
\begin{pmatrix}
\lambda_1 & 0 \\
0 & \lambda_2
\end{pmatrix}
$$
ここで
$$
P
=
\begin{pmatrix}
\boldsymbol{v}_1 & \boldsymbol{v}_2
\end{pmatrix}
$$
とすると
$$
AP
=
P
\begin{pmatrix}
\lambda_1 & 0 \\
0 & \lambda_2
\end{pmatrix}
$$
となります。$P$の逆行列を左側からかけて
$$
P^{-1}AP
=
\begin{pmatrix}
\lambda_1 & 0 \\
0 & \lambda_2
\end{pmatrix}
$$
これで対角化完了です。右辺の成分が対角の部分以外0になっています。
式をスッキリさせるために
$$
D
=
\begin{pmatrix}
\lambda_1 & 0 \\
0 & \lambda_2
\end{pmatrix}
$$
とおいて
$$
P^{-1}AP=D
$$
と表現されることが多いです。
$P$を変換行列、$D$を対角行列といいます。
対角化の計算4ステップ
それでは対角化計算の具体例を見ていきます。4ステップです。
- 固有値と固有ベクトルを求める
- 対角化可能か判定する
- 変換行列$P$を作る
- 逆行列$P^{-1}$を計算する
以下の行列$A$を対角化します。
$$
A
=
\begin{pmatrix}
1 & 2 \\
-1 & 4
\end{pmatrix}
$$
Step1. 固有値と固有ベクトルを求める
行列$A$の固有方程式は
$$
\begin{align}
\det (A-\lambda E)
&=
\begin{vmatrix}
1-\lambda & 2 \\
-1 & 4-\lambda
\end{vmatrix}
\\\\&=
(\lambda-2)(\lambda-3)
\end{align}
$$
これより固有値、固有ベクトルは
$$
\begin{array}{cc}
\lambda_1=2
&
\lambda_2=3
\end{array}
$$
$$
\begin{array}{cc}
\boldsymbol{v}_1
=
k_1
\begin{pmatrix}
2\\
1
\end{pmatrix}
&
\boldsymbol{v}_2
=
k_2
\begin{pmatrix}
1\\
1
\end{pmatrix}
\end{array}
$$
です。
Step2. 対角化可能か判定する
$n$次の行列を対角化したいときは$n$個の線形独立な固有ベクトルが必要です。
もし$n$個の線形独立な固有ベクトルがない場合は対角化できません。対角化の代わりにジョルダン標準形という形にします。
今回対角化したい行列$A$は2次です。固有ベクトルが$\boldsymbol{v}_1, \boldsymbol{v}_2$の2個あり、これらは線形独立なので今回は対角化可能です。
対角行列$D$は
$$
\begin{align}
D
&=
\begin{pmatrix}
\lambda_1 & 0 \\
0 & \lambda_2
\end{pmatrix}
\\\\&=
\begin{pmatrix}
2 & 0 \\
0 & 3
\end{pmatrix}
\end{align}
$$
となります。
Step3. 変換行列$P$を作る
変換行列$P$は線形独立な固有ベクトルを並べたものです。
線形独立な固有ベクトルは求まっているのですぐに$P$を作ってもいいですが、このままだと$P$は任意定数$k_1,k_2$が含まれた行列になってしまいこの後の計算が面倒になります。
詳細は省きますが、固有ベクトルが0にならなければ任意定数はどんな値で対角化しても同じ結果になるので、計算が楽になるようにテキトーに$k_1,k_2$の値を決めるのがおすすめです。
任意定数の値の決め方の方針は主に2種類あります。
- 変換行列が計算しやすいようテキトーに決める
- 固有ベクトルを正規化する任意定数の値を求める
対角化が目的ならテキトーに決めても正規化してもOKです。(計算を楽にするためにテキトーに決めるのがほとんどです。)
主軸変換のための対角化が目的の場合は正規化する必要があります。詳しくは対称行列の対角化のページで勉強します。
今回は$k_1=k_2=1$として、固有ベクトルを
$$
\begin{array}{cc}
\boldsymbol{v}_1
=
\begin{pmatrix}
2\\
1
\end{pmatrix}
&
\boldsymbol{v}_2
=
\begin{pmatrix}
1\\
1
\end{pmatrix}
\end{array}
$$
とします。冒頭で紹介したとおり変換行列$P$は
$$
P
=
\begin{pmatrix}
\boldsymbol{v}_1 & \boldsymbol{v}_2
\end{pmatrix}
$$
ですので
$$
P
=
\begin{pmatrix}
2 & 1 \\
1 & 1
\end{pmatrix}
$$
となります。固有ベクトルの並べ方は画像で見ると分かりやすいと思います。
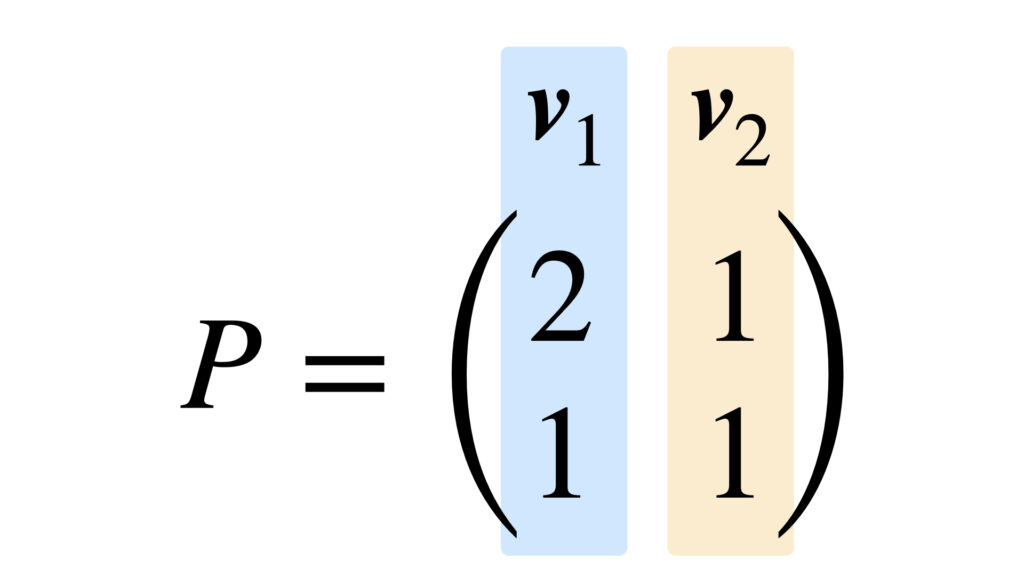
Step4. 逆行列$P^{-1}$を計算する
$P$の逆行列を計算すると
$$
P^{-1}
=
\begin{pmatrix}
1 & -1 \\
-1 & 2
\end{pmatrix}
$$
となります。
最終的に対角化の式$P^{-1}AP=D$に代入して
$$
\begin{pmatrix}
1 & -1 \\
-1 & 2
\end{pmatrix}
\begin{pmatrix}
1 & 2 \\
-1 & 4
\end{pmatrix}
\begin{pmatrix}
2 & 1 \\
1 & 1
\end{pmatrix}
=
\begin{pmatrix}
2 & 0 \\
0 & 3
\end{pmatrix}
$$
となり対角化完了です。
まとめ
行列の対角化は4ステップです。
- 固有値と固有ベクトルを求める
- 対角化可能か判定する
- 変換行列$P$を作る
- 逆行列$P^{-1}$を計算する
対角化の式は以下の式です。
$$
P^{-1}AP=D
$$





コメント欄