こんにちはコーヤです。
このページでは非同次連立1次方程式の解と自由度の関係を勉強します。線形結合や基底変換の分野で重要な知識です。
解ける式と解けない式
非同次の勉強をする前に同次の勉強を済ませておくとスムーズに進むと思います。
非同次連立1次方程式には解ける式と解けない式があります。それぞれ具体例を見ていきます。
まずは解ける非同次連立1次方程式です。
$$
\begin{align}
x+2y&=4
\\\\
3x-4y&=2
\end{align}
$$
$(x,y)=(2,1)$です。
次に解けない非同次連立1次方程式です。
$$
\begin{align}
x+2y&=4
\\\\
-2x-4y&=-8
\end{align}
$$
$(x,y)=(2,1),(4,0),(-2,3) \cdots$たくさん答えがあります。
無理やり解を出すなら任意定数$t$を用いて$(x,y)=(2t,-t+2)$となります。
厳密には「解けない」わけではありませんが「解が定まらない」ということですね。
さらに解けない式はもう1つパターンがあります。
$$
\begin{align}
x+2y&=4
\\\\
3x+6y&=4
\end{align}
$$
これは解なしになります。
これも厳密には「解けない」わけではありませんが「解が見つからない」ということです。
これを踏まえて読み進めるとスムーズにいくと思います。
拡大係数行列の作り方
今の例を使って拡大係数行列を作っていきます。やり方は簡単です。
$$
\begin{align}
x+2y&=4
\\\\
3x-4y&=2
\end{align}
$$
これを行列の形に変更して
$$
\begin{pmatrix}
1 & 2\\
3 & -4
\end{pmatrix}
\begin{pmatrix}
x\\
y
\end{pmatrix}
=
\begin{pmatrix}
4\\
2
\end{pmatrix}
$$
こうなります。
係数行列$A$は
$$
A
=
\begin{pmatrix}
1 & 2\\
3 & -4
\end{pmatrix}
$$
でしたが、拡大係数行列では右辺の値も行列の中に入れてあげます。
右辺の値を$b$とすると
$$
b
=
\begin{pmatrix}
4\\
2
\end{pmatrix}
$$
です。
拡大係数行列$A|b$は
$$
\left(
\begin{array}{cc|c}
1 & 2 & 4\\
3 & -4 & 2
\end{array}
\right)
$$
このように書きます。
解と自由度の関係
拡大係数行列から求める自由度と解の関係を調べます。
基本的には同次の時と同じような関係になるので、拡大係数行列の扱い方の注意ポイントを中心に見ていきます。
それではさっきの例で確認してみましょう。
解ける例
$$
\begin{align}
x+2y&=4
\\\\
3x-4y&=2
\end{align}
$$
この非同次連立1次方程式の拡大係数行列は
$$
\left(
\begin{array}{cc|c}
1 & 2 & 4\\
3 & -4 & 2
\end{array}
\right)
$$
でした。これの階段行列を作ると
$$
\left(
\begin{array}{cc|c}
1 & 2 & 4\\
0 & -10 & -10
\end{array}
\right)
$$
なのでランクは
$$
\mathrm{rank}\, A
=
\mathrm{rank}\, A|b
=
2
$$
です。
自由度は未知数の数から拡大係数行列のランクを引いたものなので、自由度0です。
実際に解は$(x,y)=(2,1)$でした。任意定数0個で解が表せています。
解が定まらない例
$$
\begin{align}
x+2y&=4
\\\\
-2x-4y&=-8
\end{align}
$$
この非同次連立1次方程式の拡大係数行列は
$$
\left(
\begin{array}{cc|c}
1 & 2 & 4\\
-2 & -4 & -8
\end{array}
\right)
$$
です。これの階段行列を作ると
$$
\left(
\begin{array}{cc|c}
1 & 2 & 4\\
0 & 0 & 0
\end{array}
\right)
$$
なのでランクは
$$
\mathrm{rank}\, A
=
\mathrm{rank}\, A|b
=
1
$$
です。
自由度は未知数の数から拡大係数行列のランクを引いたものなので、自由度1です。
実際に解は$(x,y)=(2t,-t+2)$でした。任意定数1個で解が表せています。
解が見つからない例
$$
\begin{align}
x+2y&=4
\\\\
3x+6y&=4
\end{align}
$$
この非同次連立1次方程式の拡大係数行列は
$$
\left(
\begin{array}{cc|c}
1 & 2 & 4\\
3 & 6 & 4
\end{array}
\right)
$$
です。これの階段行列を作ると
$$
\left(
\begin{array}{cc|c}
1 & 2 & 4\\
0 & 0 & -8
\end{array}
\right)
$$
なのでランクは
$$
\begin{align}
\mathrm{rank}\, A &= 1
\\\\
\mathrm{rank}\, A|b &= 2
\end{align}
$$
です。ここでストップ。
$$
\mathrm{rank}\, A < \mathrm{rank}\, A|b
$$
のときは解なしとなります。
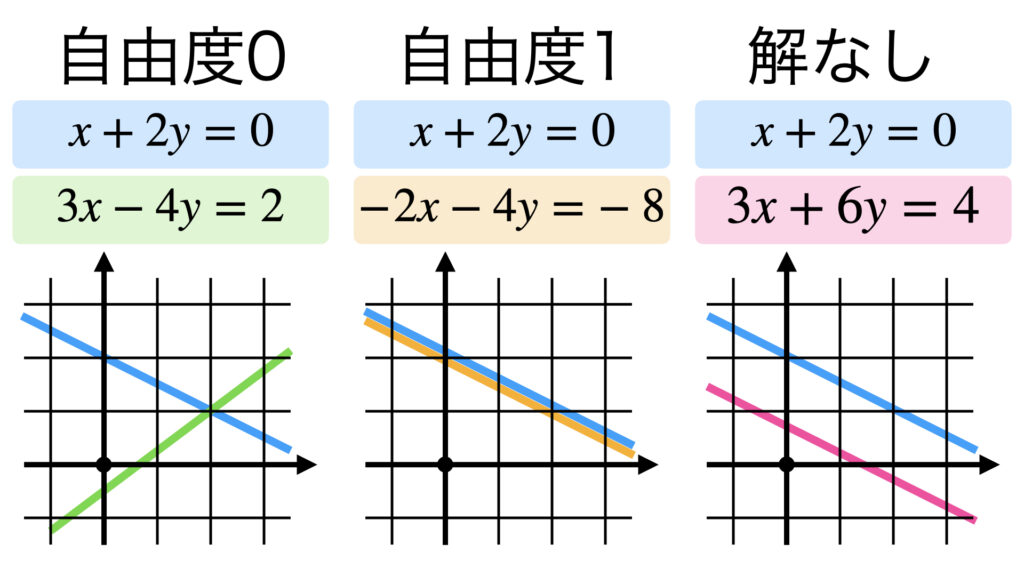
グラフで見比べればさらに自由度のイメージが付きやすいと思います。
ランクの不等式が出てきましたが
$$
\mathrm{rank}\, A > \mathrm{rank}\, A|b
$$
となる場合はありません。
$$
\begin{align}
x+2y&=4
\\\\
2x-4y&=8
\end{align}
$$
この非同次連立1次方程式の拡大係数行列は
$$
\left(
\begin{array}{cc|c}
1 & 2 & 4\\
2 & 4 & 8
\end{array}
\right)
$$
です。これの階段行列を作ると
$$
\left(
\begin{array}{cc|c}
1 & 2 & 4\\
0 & -8 & 0
\end{array}
\right)
$$
なのでランクは
$$
\mathrm{rank}\, A
=
\mathrm{rank}\, A|b
=
2
$$
です。
$$
\begin{align}
\mathrm{rank}\, A &= 2
\\\\
\mathrm{rank}\, A|b &= 1
\end{align}
$$
と勘違いしそうですが、あくまで拡大係数行列は2行3列の行列としてランクを求めます。
非同次連立1次方程式の具体例
それでは具体例4つで非同次連立1次方程式の解を求める練習をしましょう。
具体例1
$$
\begin{align}
x+2y+3z&=25
\\\\
3x+4y+2z&=41
\\\\
2x+3y+5z&=43
\end{align}
$$
この非同次連立1次方程式の解を求めます。行列形式に変形して
$$
\begin{pmatrix}
1 & 2 & 3\\
3 & 4 & 2\\
2 & 3 & 5
\end{pmatrix}
\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}
=
\begin{pmatrix}
25\\
41\\
43
\end{pmatrix}
$$
拡大係数行列を階段行列に変形してランクを求めると
$$
\left(
\begin{array}{ccc|c}
1 & 2 & 3 & 25\\
3 & 4 & 2 & 41\\
2 & 3 & 5 & 43
\end{array}
\right)
\Rightarrow
\left(
\begin{array}{ccc|c}
1 & 2 & 3 & 25\\
0 & -1 & -1 & -7\\
0 & 0 & -5 & -20
\end{array}
\right)
$$
係数行列、拡大係数行列どちらもランク3で一致しています。未知数の数は$x,y,z$の3個、ランクは3なので、自由度は0です。
つまり任意定数を使わずに解が求まります。
階段行列を使って式を書くと
$$
\begin{pmatrix}
1 & 2 & 3\\
0 & -1 & -1\\
0 & 0 & -5
\end{pmatrix}
\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}
=
\begin{pmatrix}
25\\
-7\\
-20
\end{pmatrix}
$$
行列形式から普通の方程式の形に変形して
$$
\begin{align}
x+2y+3z&=25
\\\\
-y-z&=-7
\\\\
-5z&=-20
\end{align}
$$
となります。この連立1次方程式を普通に解いて
$$
(x,y,z)=(7,3,4)
$$
となります。
具体例2
$$
\begin{align}
x+2y+3z&=25
\\\\
3x+4y+2z&=41
\\\\
4x+6y+5z&=66
\end{align}
$$
この非同次連立1次方程式の解を求めます。行列形式に変形して
$$
\begin{pmatrix}
1 & 2 & 3\\
3 & 4 & 2\\
4 & 6 & 5
\end{pmatrix}
\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}
=
\begin{pmatrix}
25\\
41\\
66
\end{pmatrix}
$$
拡大係数行列を階段行列に変形してランクを求めると
$$
\left(
\begin{array}{ccc|c}
1 & 2 & 3 & 25\\
3 & 4 & 2 & 41\\
4 & 6 & 5 & 66
\end{array}
\right)
\Rightarrow
\left(
\begin{array}{ccc|c}
1 & 2 & 3 & 25\\
0 & -2 & -7 & -34\\
0 & 0 & 0 & 0
\end{array}
\right)
$$
係数行列、拡大係数行列どちらもランク2で一致しています。未知数の数は$x,y,z$の3個、ランクは2なので、自由度は1です。
自由度が1ということは、任意定数1個で解が表せるということです。
階段行列を使って式を書くと
$$
\begin{pmatrix}
1 & 2 & 3\\
0 & -2 & -7\\
0 & 0 & 0
\end{pmatrix}
\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}
=
\begin{pmatrix}
25\\
-34\\
0
\end{pmatrix}
$$
行列形式から普通の方程式の形に変形して
$$
\begin{align}
x+2y+3z&=25
\\\\
-2y-7z&=-34
\end{align}
$$
となります。ここで任意定数$t$の出番です。
$z=2t$とおくと、2行目の方程式から$y=-7t+17$が求まります。
$y$と$z$が分かったので、1行目の方程式から$x=8t-11$が求まります。
よって
$$
(x,y,z)=(8t-11,-7t+17,2t)
$$
となります。
具体例3
$$
\begin{align}
x+2y+3z&=25
\\\\
2x+4y+6z&=50
\\\\
3x+6y+9z&=75
\end{align}
$$
この非同次連立1次方程式の解を求めます。行列形式に変形して
$$
\begin{pmatrix}
1 & 2 & 3\\
2 & 4 & 6\\
3 & 6 & 9
\end{pmatrix}
\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}
=
\begin{pmatrix}
25\\
50\\
75
\end{pmatrix}
$$
拡大係数行列を階段行列に変形してランクを求めると
$$
\left(
\begin{array}{ccc|c}
1 & 2 & 3 & 25\\
2 & 4 & 6 & 50\\
3 & 6 & 9 & 75
\end{array}
\right)
\Rightarrow
\left(
\begin{array}{ccc|c}
1 & 2 & 3 & 25\\
0 & 0 & 0 & 0\\
0 & 0 & 0 & 0
\end{array}
\right)
$$
係数行列、拡大係数行列どちらもランク1で一致しています。未知数の数は$x,y,z$の3個、ランクは1なので、自由度は2です。
自由度が2ということは、任意定数2個で解が表せるということです。
階段行列を使って式を書くと
$$
\begin{pmatrix}
1 & 2 & 3\\
0 & 0 & 0\\
0 & 0 & 0
\end{pmatrix}
\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}
=
\begin{pmatrix}
25\\
0\\
0
\end{pmatrix}
$$
行列形式から普通の方程式の形に変形して
$$
x+2y+3z=25\\
$$
となります。ここで任意定数$t_1,t_2$の出番です。
$y=t_1,z=t_2$とすると、方程式から$x=-2t_1-3t_2+25$が求まります。
よって
$$
(x,y,z)=(-2t_1-3t_2+25,t_1,t_2)
$$
となります。
具体例4
$$
\begin{align}
x+2y+3z&=25
\\\\
3x+4y+2z&=41
\\\\
2x+2y-z&=43
\end{align}
$$
この非同次連立1次方程式の解を求めます。行列形式に変形して
$$
\begin{pmatrix}
1 & 2 & 3\\
3 & 4 & 2\\
2 & 2 & -1
\end{pmatrix}
\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}
=
\begin{pmatrix}
25\\
41\\
43
\end{pmatrix}
$$
拡大係数行列を階段行列に変形してランクを求めると
$$
\left(
\begin{array}{ccc|c}
1 & 2 & 3 & 25\\
3 & 4 & 2 & 41\\
2 & 2 & -1 & 43
\end{array}
\right)
\Rightarrow
\left(
\begin{array}{ccc|c}
1 & 2 & 3 & 25\\
0 & -2 & -7 & -34\\
0 & 0 & 0 & 27
\end{array}
\right)
$$
係数行列のランクは2で、拡大係数行列のランクは3です。
拡大係数行列のランクが係数行列のランクより大きいときは解なしです。
まとめ
未知数の数から拡大係数行列のランクを引いたものが自由度です。
自由度は解の任意定数の個数を表しています。
拡大係数行列のランクが係数行列のランクより大きいときは解なしです。




コメント欄