こんにちはコーヤです。
このページでは線形写像の像空間と核空間の計算方法を勉強します。どちらも線形写像の性質を表す重要な空間です。
線形写像の意味
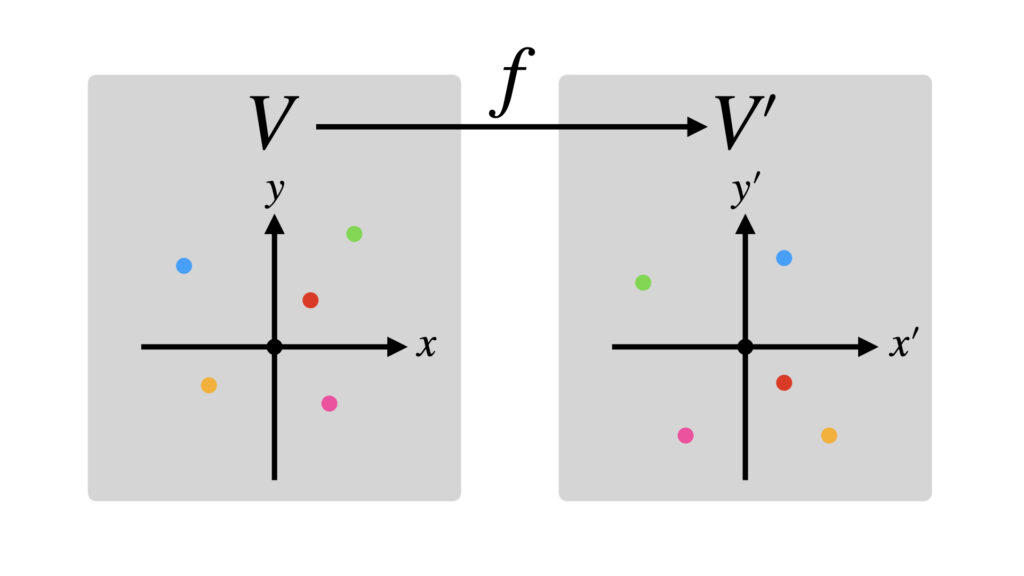
線形空間$V$から拾ってきたテキトーな元を拾ってきて、別の線形空間$V’$に引っ越しさせるというのが線形写像$f$のイメージです。
線形写像$f$によって$V$から$V’$に引っ越します、というのを式ではこう書きます。
$$
f:V \to V’
$$
引っ越しの雰囲気を画像で見るとこんな感じです。
線形写像の具体例
それでは具体例で線形写像の計算をしましょう。
引っ越し前の線形空間$V$を2次元列ベクトル$R^2$とします。座標は$x,y$です。
引っ越し先の線形空間$V’$も2次元列ベクトル$R^2$とします。座標は$x’,y’$です。
引っ越し手続きの線形写像$f$は以下のようにします。
$$
f
=
\begin{pmatrix}
0 & 1 \\
2 & 0
\end{pmatrix}
$$
この引っ越しは以下のように計算します。
$$
\begin{pmatrix}
x’ \\
y’
\end{pmatrix}
=
\begin{pmatrix}
0 & 1 \\
2 & 0
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}
$$
例えば$V$の点$(1,-1)$を引っ越しさせてみます。
$$
\begin{align}
\begin{pmatrix}
x’ \\
y’
\end{pmatrix}
&=
\begin{pmatrix}
0 & 1 \\
2 & 0
\end{pmatrix}
\begin{pmatrix}
1 \\
-1
\end{pmatrix}
\\\\&=
\begin{pmatrix}
-1 \\
2
\end{pmatrix}
\end{align}
$$
$V$の点$(1,-1)$から$V’$の点$(-1,2)$に引っ越しました。
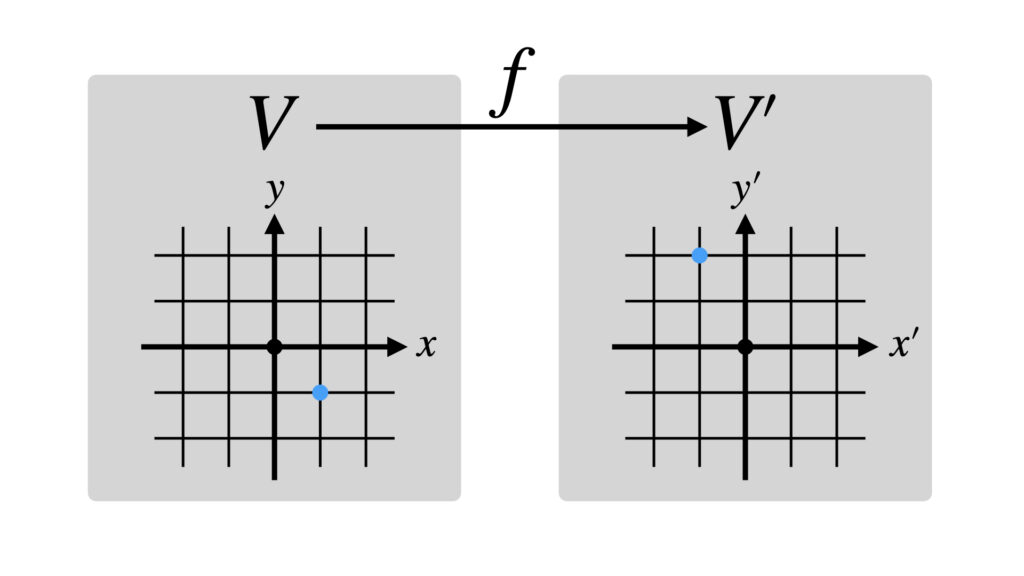
次に$V$の直線$y=2x-1$を引っ越しさせてみます。
直線$y=2x-1$上の点は任意定数$t$を用いて$(t,2t-1)$と表せます。
$$
\begin{align}
\begin{pmatrix}
x’ \\
y’
\end{pmatrix}
&=
\begin{pmatrix}
0 & 1 \\
2 & 0
\end{pmatrix}
\begin{pmatrix}
t \\
2t-1
\end{pmatrix}
\\\\&=
\begin{pmatrix}
2t-1 \\
2t
\end{pmatrix}
\end{align}
$$
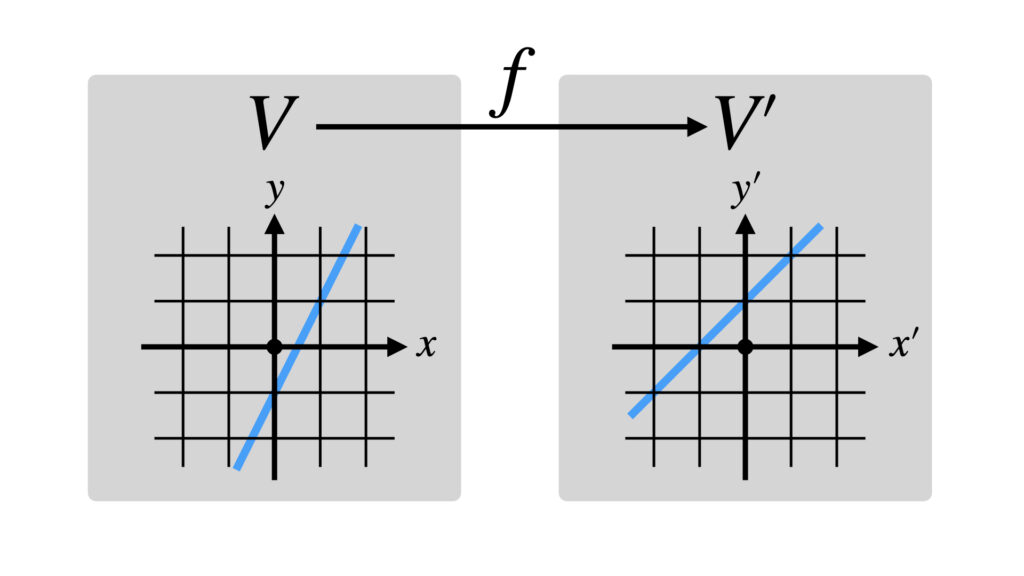
$V$の点$(t,2t-1)$から$V’$の点$(2t-1,2t)$に引っ越しました。点$(2t-1,2t)$が作る直線は$y=x+1$です。
つまり$V$の直線$y=2x-1$は$V’$の$y=x+1$に引っ越します。
像空間と核空間の意味
それでは線形写像の像空間と核空間を見ていきます。
線形写像は引っ越しみたいなものでした。
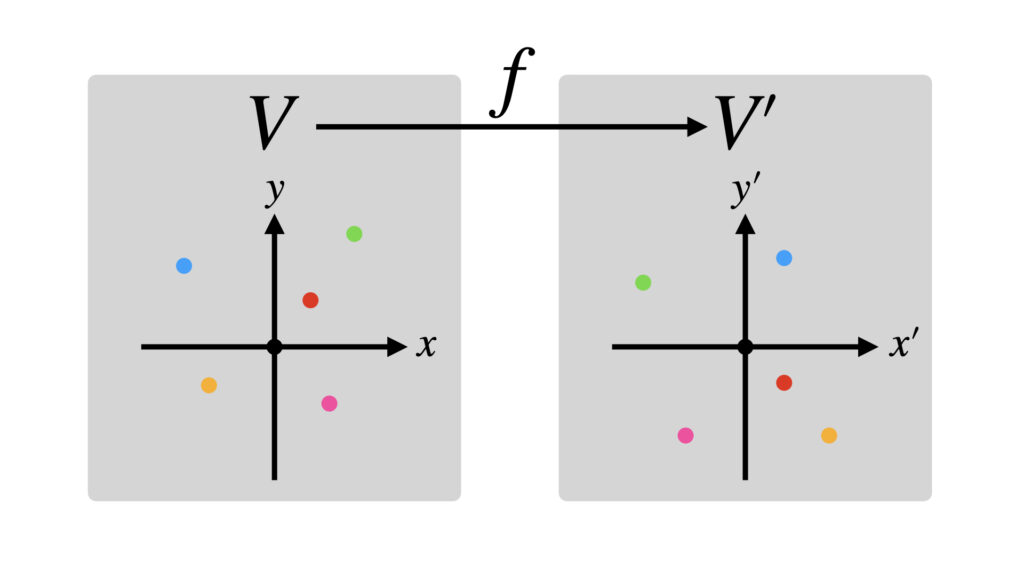
$V$全体を$V’$に線形写像したら$V’$の一部に固まったとき、その$V’$の一部が像空間$\mathrm{Im}\,f$です。
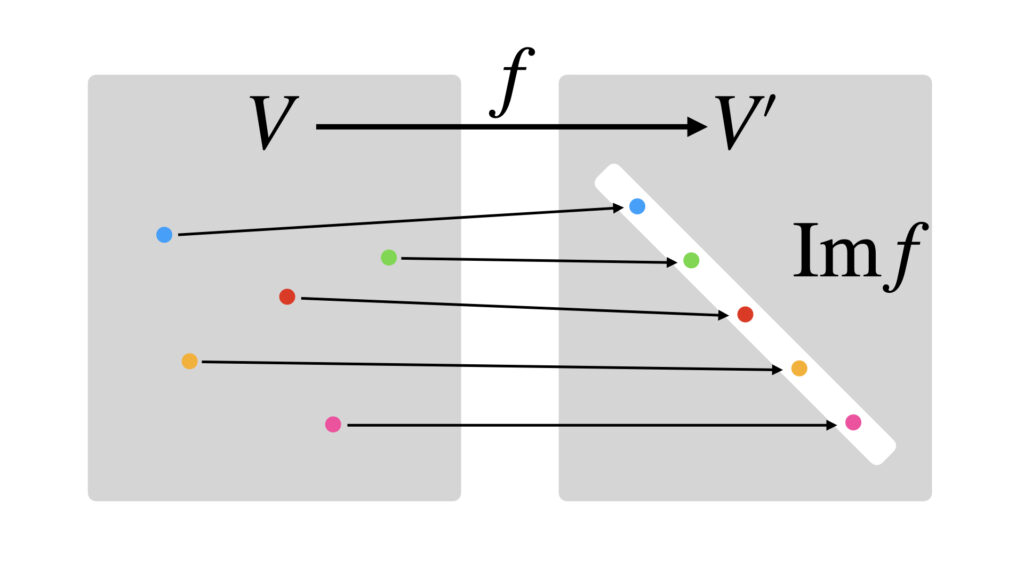
$V$の一部を写像したら$V’$の原点に固まったとき、その$V$の一部が核空間$\mathrm{Ker}\,f$です。
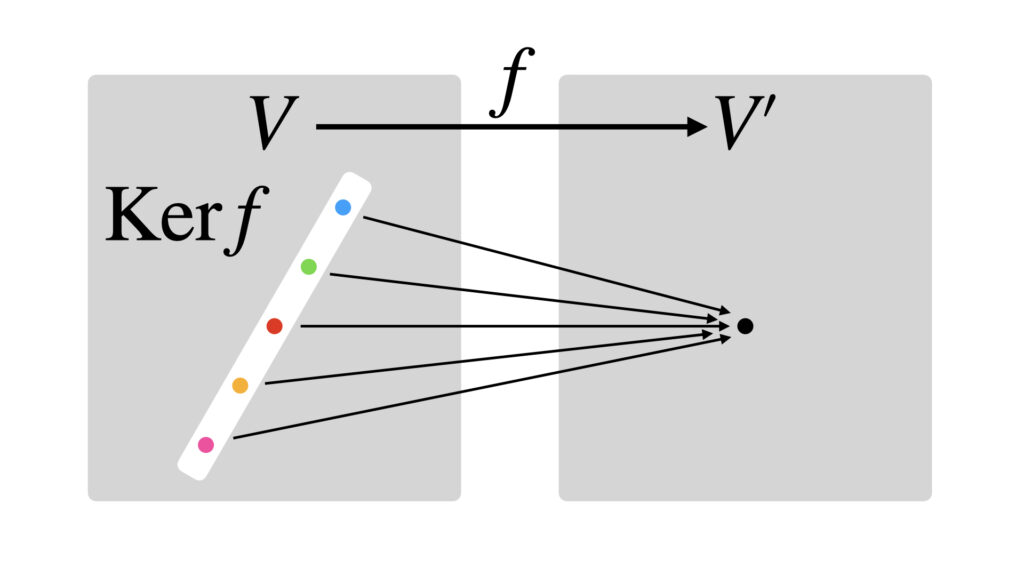
「一部」と書いたほうが雰囲気が伝わりやすいと思って書きましたが、正確には「部分空間」です。
$\mathrm{Im}\,f$は$V’$の部分空間です。$\mathrm{Ker}\,f$は$V$の部分空間です。
部分空間が不安な方は復習がてらご覧ください。
$\mathrm{Im}\,f$計算の具体例
線形写像$f:V \to V’$が以下のように定義されているとします。
$$
\begin{pmatrix}
x’ \\
y’
\end{pmatrix}
=
\begin{pmatrix}
2 & -1 \\
-2 & 1
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}
$$
$V$全体を$V’$に写像したら$V’$の一部に固まったとき、$V’$の一部が$\mathrm{Im}\,f$でした。
$V$は全体を考えるので$x,y$に制限はありません。自由な値が取れます。
$V’$は一部を考えるので$x’,y’$に制限がつきます。この制限を求めるのが$\mathrm{Im}\,f$計算のゴールです。
$\mathrm{Im}\,f$計算をするときは、最初に$\dim(\mathrm{Im}\,f)$を求めます。
$\mathrm{Im}\,f$の重要な性質の1つに、$\mathrm{Im}\,f$の次元は線形写像$f$の行列のランクと一致するという性質があります。
$$
\mathrm{rank}\,
\begin{pmatrix}
2 & -1 \\
-2 & 1
\end{pmatrix}
=
1
$$
これより$\dim (\mathrm{Im}\,f) = 1$となります。
次元が1ということは$\mathrm{Im}\,f$は直線です。また、直線ということは任意定数1個で表すことができます。
冒頭の例の点$(2t-1,2t)$が作る直線は$y=x+1$になる、というのを逆に捉えます。
直線$y=x+1$は任意定数$t$の1個で表すことができています。
任意定数2個なら平面、3個なら空間となります。
以上より$\mathrm{Im}\,f$は直線かつ任意定数1個という情報を得ました。
それでは線形写像$f$を方程式の形に変形して
$$
\begin{align}
x’&=2x-y
\\\\
y’&=-2x+y
\end{align}
$$
です。$x’,y’$の制限を求めるのがゴールなので$x,y$はいらない文字です。任意定数が1個使えることが分かっているので$2x-y=t$として$x,y$をまとめると
$$
\begin{align}
x’&=t
\\\\
y’&=-t
\end{align}
$$
となります。この2式から$x’,y’$は
$$
y’=-x’
$$
の制限がかかることが分かります。
これより$\mathrm{Im}\,f$は$y’=-x’$の直線です。
次元定理の意味
$\mathrm{Ker}\,f$計算で使う次元定理は以下の公式です。
$$
\dim V =\dim (\mathrm{Im}\,f) +\dim (\mathrm{Ker}\,f)
$$
今の例だと$V$は$x,y$の2次元空間なので$\dim V=2$です。$\dim(\mathrm{Im}f)$は計算したとおり$\dim(\mathrm{Im}f)=1$です。
$\mathrm{Ker}\,f$はまだ分かりませんが、次元定理より$\dim(\mathrm{Ker}f)=1$であることがわかりました。
$\mathrm{Ker}\,f$は1次元、つまり直線であるという情報を持った状態で計算に進みます。
$\mathrm{Ker}\,f$計算の具体例
$\mathrm{Im}\,f$の例と同じ$f:V \to V’$を考えます。
$$
\begin{pmatrix}
x’ \\
y’
\end{pmatrix}
=
\begin{pmatrix}
2 & -1 \\
-2 & 1
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}
$$
$V$の一部を写像したら$V’$の原点に固まったとき、$V$の一部が$\mathrm{Ker}\,f$でした。
$V$は一部を考えるので$x,y$に制限がつきます。この制限を求めるのが$\mathrm{Ker}\,f$計算のゴールです。
$V’$は原点を考えるので$(x’,y’)=(0,0)$です。
線形写像の式に$(x’,y’)=(0,0)$を代入して
$$
\begin{pmatrix}
0 \\
0
\end{pmatrix}
=
\begin{pmatrix}
2 & -1 \\
-2 & 1
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}
$$
これは同次連立1次方程式の形になっています。
同次連立1次方程式や自由度が不安な方はご覧ください。
この同次連立1次方程式から得られる式は
$$
2x-y=0
$$
です。
$\mathrm{Ker}\,f$は直線だと分かっているので、この式を直線だとわかるように変形して
$$
y=2x
$$
となります。
これより$\mathrm{Ker}\,f$は$y=2x$の直線です。
$\mathrm{Im}\,f$と$\mathrm{Ker}\,f$の検算
$V$全体を$V’$に線形写像したら$V’$の一部に固まったとき、その$V’$の一部が$\mathrm{Im}\,f$でした。
$V$の一部を写像したら$V’$の原点に固まったとき、その$V$の一部が$\mathrm{Ker}\,f$でした。
計算が終わったので、線形写像の様子を確認して$V$と$V’$の引っ越しの様子を見てみましょう。
$\mathrm{Im}\,f$の検算
$V$から適当に点を選びます。今回は$(1,0)$$(0,1)$$(-1,0)$$(0,-1)$とします。
4点がどこに移されるかそれぞれ計算すると
$$
\begin{pmatrix}
x’ \\
y’
\end{pmatrix}
=
\begin{pmatrix}
2 & -1 \\
-2 & 1
\end{pmatrix}
\begin{pmatrix}
1 \\
0
\end{pmatrix}
=
\begin{pmatrix}
2 \\
-2
\end{pmatrix}
$$
$$
\begin{pmatrix}
x’ \\
y’
\end{pmatrix}
=
\begin{pmatrix}
2 & -1 \\
-2 & 1
\end{pmatrix}
\begin{pmatrix}
0 \\
1
\end{pmatrix}
=
\begin{pmatrix}
-1 \\
1
\end{pmatrix}
$$
$$
\begin{pmatrix}
x’ \\
y’
\end{pmatrix}
=
\begin{pmatrix}
2 & -1 \\
-2 & 1
\end{pmatrix}
\begin{pmatrix}
-1 \\
0
\end{pmatrix}
=
\begin{pmatrix}
-2 \\
2
\end{pmatrix}
$$
$$
\begin{pmatrix}
x’ \\
y’
\end{pmatrix}
=
\begin{pmatrix}
2 & -1 \\
-2 & 1
\end{pmatrix}
\begin{pmatrix}
0 \\
-1
\end{pmatrix}
=
\begin{pmatrix}
1 \\
-1
\end{pmatrix}
$$
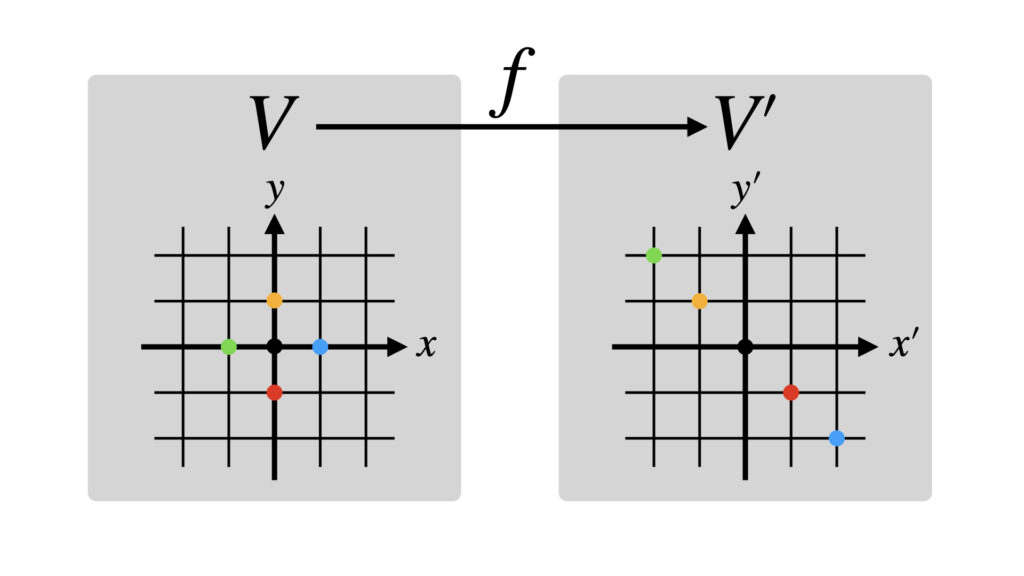
たしかに$y’=-x’$の直線上に移されていることが分かります。
$\mathrm{Ker}\,f$の検算
$y=2x$上から適当に点を選びます。今回は$(0,0)$$(1,2)$$(-1,-2)$とします。
3点がどこに移されるかそれぞれ計算すると
$$
\begin{pmatrix}
x’ \\
y’
\end{pmatrix}
=
\begin{pmatrix}
2 & -1 \\
-2 & 1
\end{pmatrix}
\begin{pmatrix}
0 \\
0
\end{pmatrix}
=
\begin{pmatrix}
0 \\
0
\end{pmatrix}
$$
$$
\begin{pmatrix}
x’ \\
y’
\end{pmatrix}
=
\begin{pmatrix}
2 & -1 \\
-2 & 1
\end{pmatrix}
\begin{pmatrix}
1 \\
2
\end{pmatrix}
=
\begin{pmatrix}
0 \\
0
\end{pmatrix}
$$
$$
\begin{pmatrix}
x’ \\
y’
\end{pmatrix}
=
\begin{pmatrix}
2 & -1 \\
-2 & 1
\end{pmatrix}
\begin{pmatrix}
-1 \\
-2
\end{pmatrix}
=
\begin{pmatrix}
0 \\
0
\end{pmatrix}
$$
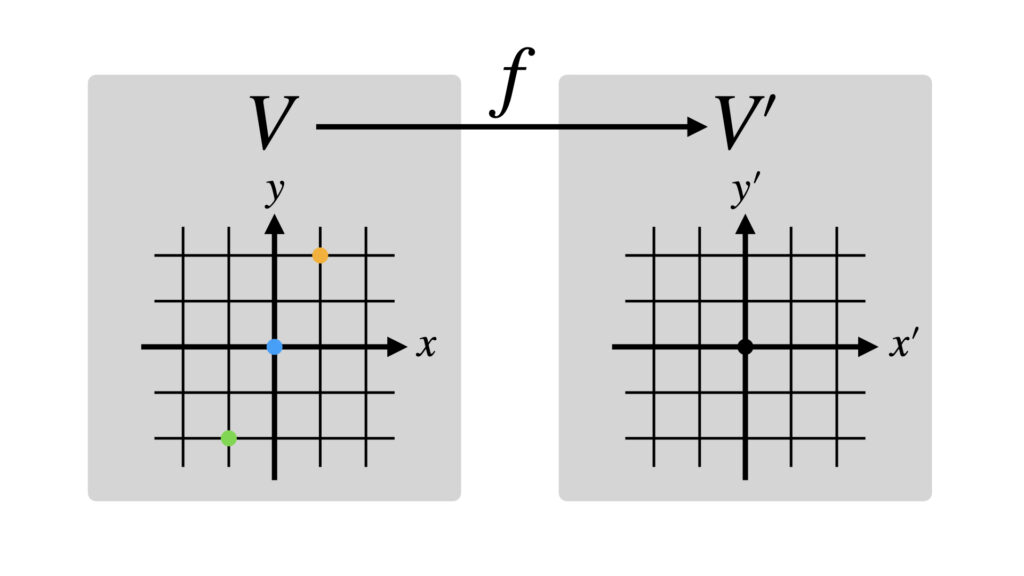
たしかに$y=2x$の直線上の点が$(x’,y’)=(0,0)$移されていることが分かります。
まとめ
線形空間$V$から線形空間$V’$に対応させるのが線形写像$f$です。
$V$全体を$V’$に写像したら$V’$の一部に固まったとき、$V’$の一部が$\mathrm{Im}f$です。
$V$の一部を写像したら$V’$の原点に固まったとき、$V$の一部が$\mathrm{Ker}\,f$です。
次元定理は以下の公式です。
$$
\dim V =\dim (\mathrm{Im}\,f) +\dim (\mathrm{Ker}\,f)
$$





コメント欄