こんにちはコーヤです。
このページでは同次連立1次方程式の解と自由度の関係を勉強します。線形独立の判定、固有ベクトル、核空間などの場面で必要な線形代数の重要な知識です。
同次・非同次の分類
同次と非同次は右辺が全部0かどうかで分類されます。
$$
\begin{align}
x+2y&=0
\\\\
3x-4y&=0
\end{align}
$$
$$
\begin{align}
x+2y&=4
\\\\
3x-4y&=2
\end{align}
$$
上の2式は同次連立1次方程式、下の2式は非同次連立1次方程式です。
このページでは同次連立1次方程式を扱います。非同次連立1次方程式は次のページで勉強します。
解ける式と解けない式
同次連立1次方程式には解ける式と解けない式があります。それぞれ具体例を見ていきます。
まずは解ける同次連立1次方程式です。
$$
\begin{align}
x+2y&=0
\\\\
3x-4y&=0
\end{align}
$$
$(x,y)=(0,0)$です。
次に解けない同次連立1次方程式です。
$$
\begin{align}
x+2y&=0
\\\\
-2x-4y&=0
\end{align}
$$
$(x,y)=(0,0),(2,-1),(-2,1) \cdots$たくさん答えがあります。
無理やり解を出すなら任意定数$t$を用いて$(x,y)=(2t,-t)$となります。
厳密には「解けない」わけではありませんが「解が定まらない」ということです。
これを踏まえて読み進めるとスムーズにいくと思います。
自由度の求め方
未知数の数から係数行列のランクを引いたのが自由度です。
さっきの例を使って自由度を求めます。
解ける例
$$
\begin{align}
x+2y&=0
\\\\
3x-4y&=0
\end{align}
$$
これを行列の形に変更して
$$
\begin{pmatrix}
1 & 2\\
3 & -4
\end{pmatrix}
\begin{pmatrix}
x\\
y
\end{pmatrix}
=
\begin{pmatrix}
0\\
0
\end{pmatrix}
$$
こうなります。
係数行列$A$を
$$
A
=
\begin{pmatrix}
1 & 2\\
3 & -4
\end{pmatrix}
$$
とすると$\mathrm{rank}\, A=2$です。
この同次連立1次方程式は未知数の数は$x,y$の2個、ランクは2です。
自由度は未知数の数からランクを引いたものなので、自由度0です。
解けない例
$$
\begin{align}
x+2y&=0
\\\\
-2x-4y&=0
\end{align}
$$
これを行列の形に変更して
$$
\begin{pmatrix}
1 & 2\\
-2 & -4
\end{pmatrix}
\begin{pmatrix}
x\\
y
\end{pmatrix}
=
\begin{pmatrix}
0\\
0
\end{pmatrix}
$$
こうなります。
係数行列$B$を
$$
B
=
\begin{pmatrix}
1 & 2\\
-2 & -4
\end{pmatrix}
$$
とすると$\mathrm{rank}\, B=1$です。
この同次連立1次方程式は未知数の数は$x,y$の2個、ランクは1です。
自由度は未知数の数からランクを引いたものなので、自由度1です。
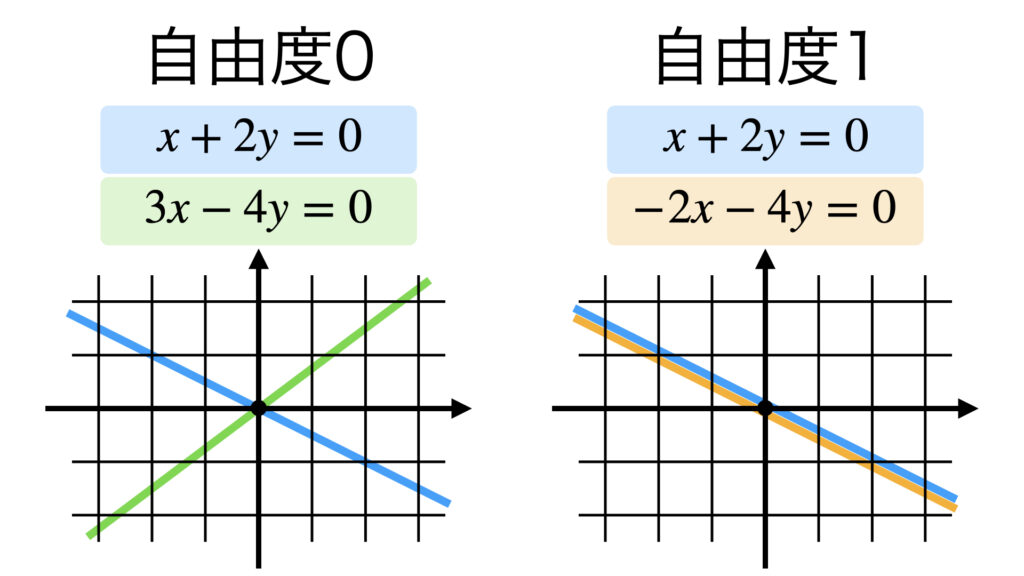
解と自由度の関係
自由度は解の任意定数の個数を表します。
$$
\begin{align}
x+2y&=0
\\\\
3x-4y&=0
\end{align}
$$
この同次連立1次方程式の自由度は0でした。
解は$(x,y)=(0,0)$です。任意定数0個で解が求まっています。
$$
\begin{align}
x+2y&=0
\\\\
-2x-4y&=0
\end{align}
$$
この同次連立1次方程式の自由度は1でした。
解は$(x,y)=(2t,-t)$です。任意定数1個で解が求まっています。
2つの例を見ると、たしかに自由度と解の任意定数の個数が一致しています。
グラフで見比べればさらに自由度のイメージが付きやすいと思います。
同次連立1次方程式の具体例
それでは具体例3つで同次連立1次方程式の解を求める練習をしましょう。
具体例1
$$
\begin{align}
x+2y+3z&=0
\\\\
3x+4y+2z&=0
\\\\
2x+3y+5z&=0
\end{align}
$$
この同次連立1次方程式の解を求めます。行列形式に変形して
$$
\begin{pmatrix}
1 & 2 & 3\\
3 & 4 & 2\\
2 & 3 & 5
\end{pmatrix}
\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}
=
\begin{pmatrix}
0\\
0\\
0
\end{pmatrix}
$$
係数行列を階段行列に変形してランクを求めると
$$
\begin{pmatrix}
1 & 2 & 3\\
3 & 4 & 2\\
2 & 3 & 5
\end{pmatrix}
\Rightarrow
\begin{pmatrix}
1 & 2 & 3\\
0 & -1 & -1\\
0 & 0 & -5
\end{pmatrix}
$$
この行列はランク3です。未知数の数は$x,y,z$の3個、ランクは3なので、自由度は0です。
つまり任意定数を使わずに解が求まります。
階段行列を使って式を書くと
$$
\begin{pmatrix}
1 & 2 & 3\\
0 & -1 & -1\\
0 & 0 & -5
\end{pmatrix}
\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}
=
\begin{pmatrix}
0\\
0\\
0
\end{pmatrix}
$$
行列形式から普通の方程式の形に変形して
$$
\begin{align}
x+2y+3z&=0
\\\\
-y-z&=0
\\\\
-5z&=0
\end{align}
$$
となります。この連立1次方程式を普通に解いて
$$
(x,y,z)=(0,0,0)
$$
となります。
具体例2
$$
\begin{align}
x+2y+3z&=0
\\\\
3x+4y+2z&=0
\\\\
4x+6y+5z&=0
\end{align}
$$
この同次連立1次方程式の解を求めます。行列形式に変形して
$$
\begin{pmatrix}
1 & 2 & 3\\
3 & 4 & 2\\
4 & 6 & 5
\end{pmatrix}
\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}
=
\begin{pmatrix}
0\\
0\\
0
\end{pmatrix}
$$
係数行列を階段行列に変形してランクを求めると
$$
\begin{pmatrix}
1 & 2 & 3\\
3 & 4 & 2\\
4 & 6 & 5
\end{pmatrix}
\Rightarrow
\begin{pmatrix}
1 & 2 & 3\\
0 & -2 & -7\\
0 & 0 & 0
\end{pmatrix}
$$
この行列はランク2です。未知数の数は$x,y,z$の3個、ランクは2なので、自由度は1です。
自由度が1ということは、任意定数1個で解が表せるということです。
階段行列を使って式を書くと
$$
\begin{pmatrix}
1 & 2 & 3\\
0 & -2 & -7\\
0 & 0 & 0
\end{pmatrix}
\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}
=
\begin{pmatrix}
0\\
0\\
0
\end{pmatrix}
$$
行列形式から普通の方程式の形に変形して
$$
\begin{align}
x+2y+3z&=0
\\\\
-2y-7z&=0
\end{align}
$$
となります。ここで任意定数$t$の出番です。
$z=2t$とおくと、2行目の方程式から$y=-7t$が求まります。
$y$と$z$が分かったので、1行目の方程式から$x=8t$が求まります。
よって
$$
(x,y,z)=(8t,-7t,2t)
$$
となります。
具体例3
$$
\begin{align}
x+2y+3z&=0
\\\\
2x+4y+6z&=0
\\\\
3x+6y+9z&=0
\end{align}
$$
この同次連立1次方程式の解を求めます。行列形式に変形して
$$
\begin{pmatrix}
1 & 2 & 3\\
2 & 4 & 6\\
3 & 6 & 9
\end{pmatrix}
\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}
=
\begin{pmatrix}
0\\
0\\
0
\end{pmatrix}
$$
係数行列を階段行列に変形してランクを求めると
$$
\begin{pmatrix}
1 & 2 & 3\\
3 & 4 & 2\\
4 & 6 & 5
\end{pmatrix}
\Rightarrow
\begin{pmatrix}
1 & 2 & 3\\
0 & 0 & 0\\
0 & 0 & 0
\end{pmatrix}
$$
この行列はランク1です。未知数の数は$x,y,z$の3個、ランクは1なので、自由度は2です。
自由度が2ということは、任意定数2個で解が表せるということです。
階段行列を使って式を書くと
$$
\begin{pmatrix}
1 & 2 & 3\\
0 & 0 & 0\\
0 & 0 & 0
\end{pmatrix}
\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}
=
\begin{pmatrix}
0\\
0\\
0
\end{pmatrix}
$$
行列形式から普通の方程式の形に変形して
$$
x+2y+3z=0
$$
となります。ここで任意定数$t_1,t_2$の出番です。
$y=t_1,z=t_2$とすると、方程式から$x=-2t_1-3t_2$が求まります。
よって
$$
(x,y,z)=(-2t_1-3t_2,t_1,t_2)
$$
となります。
まとめ
未知数の数から係数行列のランクを引いたものが自由度です。
自由度は解の任意定数の個数を表しています。




コメント欄