直交行列を用いた主軸変換

こんにちはコーヤです。

このページでは直交行列を用いた主軸変換を4ステップに分けて勉強します。斜めになった図形をまっすぐに直せるようになります。微積の分野で極値を見つけるときにも必要な計算です。

主軸変換の目的
二次形式と標準形の意味
主軸変換の計算4ステップ
Step1. 対称行列を用いた行列の形に変形する
Step2. 対称行列の対角化を行う
Step3. 旧軸と新軸の関係式を作る
Step4. 行列の形から式の形へ変形する
まとめ

主軸変換の目的

$\begin{matrix} (1) & 3 x^{2} + 4 x y + 3 y^{2} = 5 \end{matrix}$

この式がどんな図形か分かりますか？答えは楕円です。

式を見ただけでは分かりませんが、実際にグラフを書くと楕円になっています。

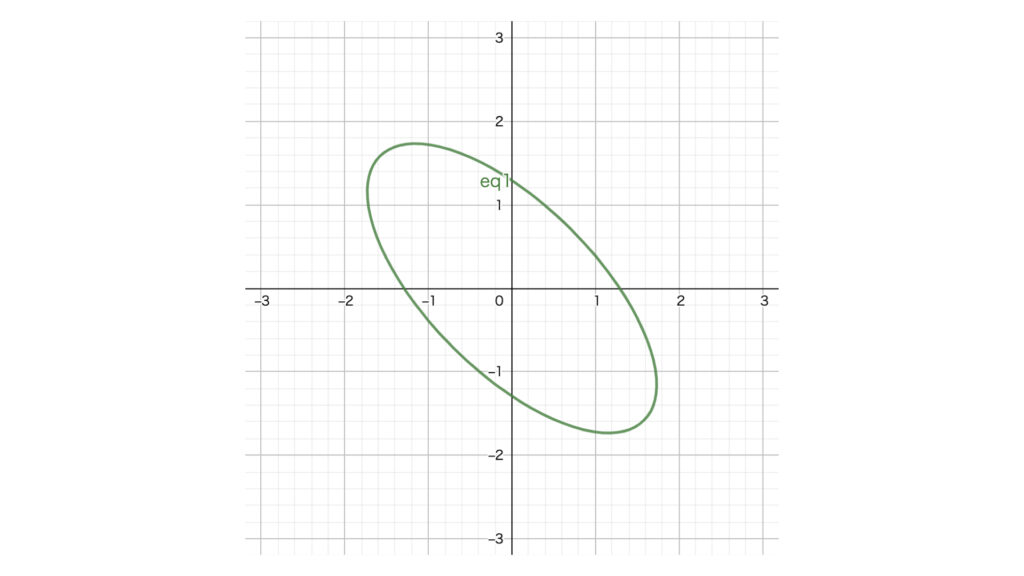
$x, y$ 軸から見ると斜めになっているので、新しく $x^{'}, y^{'}$ 軸を作ります。

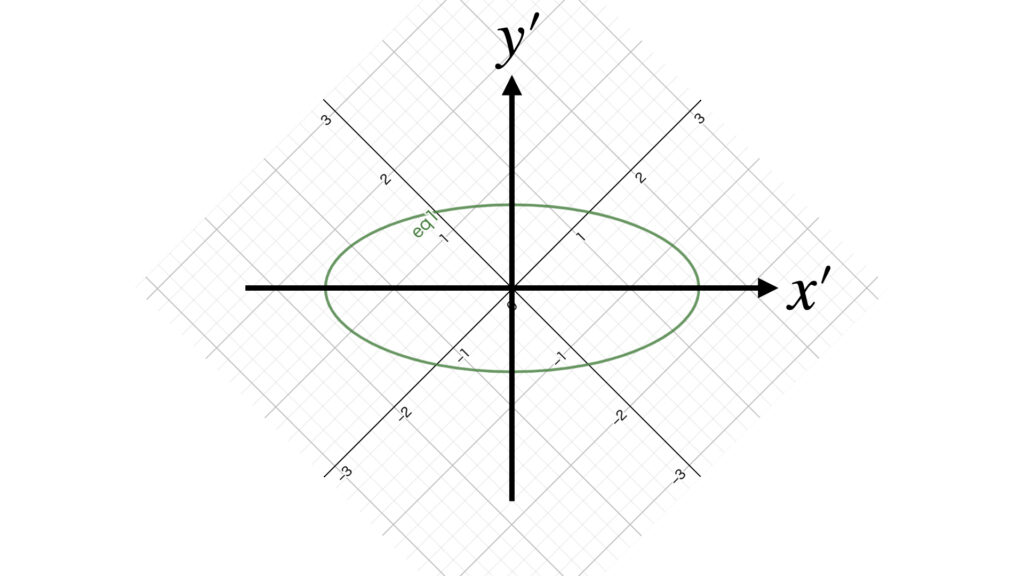
こうすると見慣れたまっすぐな楕円になります。この楕円の式は

$\begin{matrix} (2) & x^{' 2} + 5 y^{' 2} = 5 \end{matrix}$

です。

このように $x, y$ 軸では見にくいものを $x^{'}, y^{'}$ 軸に変換して見やすくする、というのが主軸変換の目的です。

そして式(1)から式(2)に変換するのに必要な知識が直交行列を用いた行列の対角化です。

二次形式と標準形の意味

具体的な計算に入る前に主軸変換の分野で出てくる言葉の意味の紹介です。計算方法が知りたい方は飛ばしてください。

$\begin{aligned} (1) & 3 x^{2} + 4 x y + 3 y^{2} & = 5 \\ (2) & x^{' 2} + 5 y^{' 2} & = 5 \end{aligned}$

式(1)のように変数が混ざった積（ $4 x y$ のところ）がある形を二次形式といいます。

式(2)には変数が混ざった積がありません。このような形を標準形といいます。

主軸変換は二次形式から標準形への変換です。

一般的に二次形式は見にくい形、標準形は見やすい形です。斜めの楕円よりまっすぐな楕円のほうが見やすいですよね。

主軸変換の計算4ステップ

主軸変換の計算は4ステップです。

対称行列を用いた行列の形に変形する
対称行列の対角化を行う
旧軸と新軸の関係式を作る
行列の形から式の形へ変形する

冒頭の例の式を再掲します。

$\begin{aligned} (1) & 3 x^{2} + 4 x y + 3 y^{2} & = 5 \\ (2) & x^{' 2} + 5 y^{' 2} & = 5 \end{aligned}$

この変換をやってみます。

Step1. 対称行列を用いた行列の形に変形する

式(1)の左辺を対称行列を用いた行列の形で表すと

$3 x^{2} + 4 x y + 3 y^{2} = (\begin{matrix} x & y \end{matrix}) (\begin{matrix} 3 & 2 \\ 2 & 3 \end{matrix}) (\begin{matrix} x \\ y \end{matrix})$

となります。

$S = (\begin{matrix} 3 & 2 \\ 2 & 3 \end{matrix})$

として式を書き換えます。

$\begin{matrix} (3) & 3 x^{2} + 4 x y + 3 y^{2} = (\begin{matrix} x & y \end{matrix}) S (\begin{matrix} x \\ y \end{matrix}) \end{matrix}$

すっきりした形になりました。

ここでの注意ポイントは対称行列を作るように行列の値を決めることです。

$3 x^{2} + 4 x y + 3 y^{2} = (\begin{matrix} x & y \end{matrix}) (\begin{matrix} 3 & 4 \\ 0 & 3 \end{matrix}) (\begin{matrix} x \\ y \end{matrix})$

このように行列の値を決めても式変形は満たしていますが、主軸変換はできなくなってしまいます。

Step2. 対称行列の対角化を行う

$S = (\begin{matrix} 3 & 2 \\ 2 & 3 \end{matrix})$

この対称行列の対角化を行います。

$\begin{array}{ccc} U = \frac{1}{\sqrt{2}} (\begin{matrix} 1 & 1 \\ - 1 & 1 \end{matrix}) & ^{t} U = \frac{1}{\sqrt{2}} (\begin{matrix} 1 & - 1 \\ 1 & 1 \end{matrix}) & D = (\begin{matrix} 1 & 0 \\ 0 & 5 \end{matrix}) \end{array}$

を用いて $^{t} U S U = D$ となります。

詳しい計算は対称行列の対角化のページで行っています。不安な方はご覧ください。

対称行列の対角化

直交行列を使用して対称行列の対角化を行います。対角化の特殊な場合で、主軸変換に応用されます。

Step3. 旧軸と新軸の関係式を作る

変換前の $x, y$ 軸と変換後の $x^{'}, y^{'}$ 軸の関係式を作ります。

$\begin{matrix} (4) & (\begin{matrix} x \\ y \end{matrix}) = U (\begin{matrix} x^{'} \\ y^{'} \end{matrix}) \end{matrix}$

これは主軸変換の公式みたいなものです。このように $x, y$ 軸と $x^{'}, y^{'}$ 軸を設定してあげると、この後の工程でうまく計算できるようになります。

式(4)からもう1つの関係式を導けます。

$\begin{aligned} (\begin{array}{c} x & y \end{array}) & =^{t} (\begin{array}{c} x \\ y \end{array}) \\ =^{t} {U (\begin{array}{c} x^{'} \\ y^{'} \end{array})} \\ =^{t} (\begin{array}{c} x^{'} \\ y^{'} \end{array})^{t} U \\ (5) & = (\begin{array}{c} x^{'} & y^{'} \end{array})^{t} U \end{aligned}$

です。途中の式変形で転置の性質である $^{t} (A B) =^{t} B^{t} A$ を使っています。

Step4. 行列の形から式の形へ変形する

最後のステップです。式(3)に式(4)(5)を代入して、行列の形から式の形へ変形します。

$\begin{aligned} 3 x^{2} + 4 x y + 3 y^{2} & = (\begin{array}{c} x & y \end{array}) S (\begin{array}{c} x \\ y \end{array}) \\ = (\begin{array}{c} x^{'} & y^{'} \end{array})^{t} U S U (\begin{array}{c} x^{'} \\ y^{'} \end{array}) \\ = (\begin{array}{c} x^{'} & y^{'} \end{array}) D (\begin{array}{c} x^{'} \\ y^{'} \end{array}) \\ = (\begin{array}{c} x^{'} & y^{'} \end{array}) (\begin{array}{c} 1 & 0 \\ 0 & 5 \end{array}) (\begin{array}{c} x^{'} \\ y^{'} \end{array}) \\ = x^{' 2} + 5 y^{' 2} \end{aligned}$

となります。途中で対角化の式 $^{t} U S U = D$ を使いました。

これで主軸変換完了です。

$\begin{aligned} (1) & 3 x^{2} + 4 x y + 3 y^{2} & = 5 \\ (2) & x^{' 2} + 5 y^{' 2} & = 5 \end{aligned}$

式(1)から式(2)へ変換できました。参考として式(1)と式(2)を同じ軸に書いたグラフを載せます。

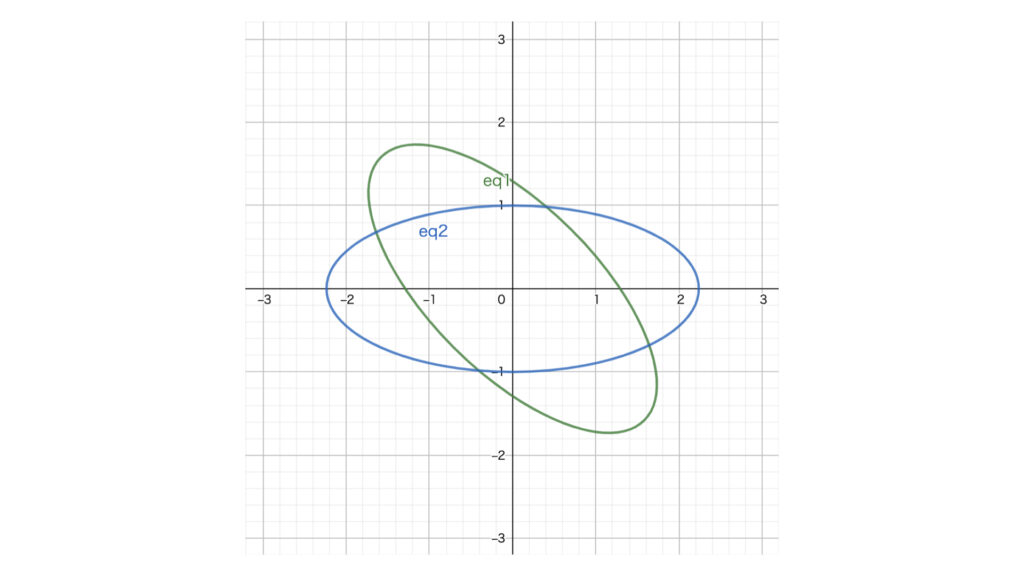
このグラフを見ると、式(2)の楕円に比べて式(1)の楕円は $- 45^{\circ}$ 回転しています。

$- 45^{\circ}$ 回転の種は $U$ に隠されています。 $U$ を変形すると

$\begin{aligned} U & = \frac{1}{\sqrt{2}} (\begin{array}{c} 1 & 1 \\ - 1 & 1 \end{array}) \\ = (\begin{array}{c} \cos (- 45^{\circ}) & - \sin (- 45^{\circ}) \\ \sin (- 45^{\circ}) & \cos (- 45^{\circ}) \end{array}) \end{aligned}$

となり $- 45^{\circ}$ の回転行列になっています。

式(4)で変換前の $x, y$ 軸と変換後の $x^{'}, y^{'}$ 軸の関係式を作りました。

$\begin{matrix} (4) & (\begin{matrix} x \\ y \end{matrix}) = U (\begin{matrix} x^{'} \\ y^{'} \end{matrix}) \end{matrix}$

これは $x, y$ 軸と $x^{'}, y^{'}$ 軸を $- 45^{\circ}$ 回転した軸が等しいという意味です。

軸を $- 45^{\circ}$ 回転させれば斜めの楕円がまっすぐな楕円になる、とも読み取れますので、もともと楕円も軸から $- 45^{\circ}$ 分だけ斜めになっていたということです。

まとめ

主軸変換は4ステップです。

対称行列を用いた行列の形に変形する
対称行列の対角化を行う
旧軸と新軸の関係式を作る
行列の形から式の形へ変形する

エルミート行列の対角化

ユニタリ行列を使用してエルミート行列の対角化を行います。ついに行列は複素数の世界へ突入します。

対称行列の対角化

直交行列を使用して対称行列の対角化を行います。対角化の特殊な場合で、主軸変換に応用されます。

直交行列を用いた主軸変換

主軸変換の目的

二次形式と標準形の意味

主軸変換の計算4ステップ

Step1. 対称行列を用いた行列の形に変形する

Step2. 対称行列の対角化を行う

Step3. 旧軸と新軸の関係式を作る

Step4. 行列の形から式の形へ変形する

まとめ

次のページ

前のページ

目次

コメント欄