こんにちはコーヤです。
このページではランクの求め方を勉強します。連立方程式の分野で重要な自由度や、線形空間の分野で重要な像空間の次元など、ランクが役立つ場面はたくさんあります。
ランクの求め方
行列のランクを求めるためには階段行列が必要です。
階段行列のイメージはこんな感じです。
$$
\begin{pmatrix}
a_{11} & a_{12} & a_{13} & a_{14} & \cdots & a_{1n} \\
0 & a_{22} & a_{23} & a_{24} & \cdots & a_{2n} \\
0 & 0 & 0 & a_{34} & \cdots & a_{3n} \\
\vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\
0 & 0 & 0 & 0 & \cdots & a_{kn} \\
0 & 0 & 0 & 0 & \cdots & 0 \\
\vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\
0 & 0 & 0 & 0 & \cdots & 0
\end{pmatrix}
$$
厳密にこの例を見るというより、左下に0を固めてくイメージが伝われば大丈夫です。
階段行列をつくったら0以外の成分が含まれている行数を数えます。
上の例だと$k$行です。この$k$がランクです。
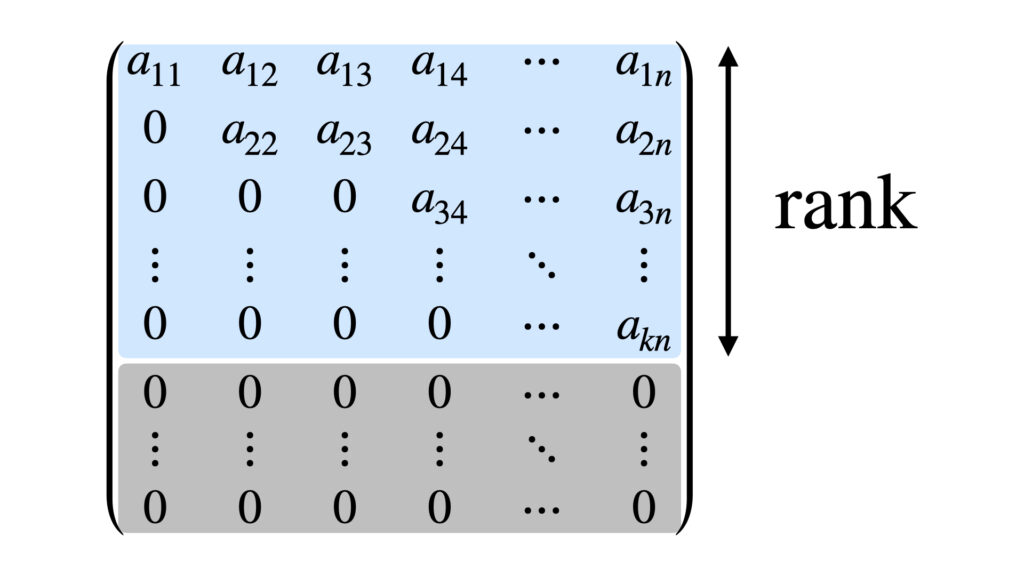
階段行列の具体例
階段行列さえ作れればランクは行数を数えるだけです。
階段行列を作るとき、つまり左下に0を固めるときに使うのが行基本変形と列基本変形です。
基本変形のおさらいです。基本変形には3つのルールがあります。
- 2つの行or列を入れ替える
- 1つの行or列をスカラー倍する
- 1つの行or列をスカラー倍して他の行or列に足す
詳しくは行基本変形のページをご覧ください。
それでは具体例3つで階段行列を作る練習をしましょう。
具体例1
$$
A
=
\begin{pmatrix}
1 & 2 & 3\\
3 & 4 & 2\\
2 & 3 & 5
\end{pmatrix}
$$
まずは左下の3行1列を0にしたいので、ルール3で1行目を-2倍して3行目に足します。
$$
\begin{pmatrix}
1 & 2 & 3\\
3 & 4 & 2\\
0 & -1 & -1
\end{pmatrix}
$$
左下に0が1個できました。次は2行1列も0にします。
ルール3で1行目を-3倍して2行目に足します。
$$
\begin{pmatrix}
1 & 2 & 3\\
0 & -2 & -7\\
0 & -1 & -1
\end{pmatrix}
$$
ルール1で2行目と3行目を入れ替えます。
$$
\begin{pmatrix}
1 & 2 & 3\\
0 & -1 & -1\\
0 & -2 & -7
\end{pmatrix}
$$
ルール3で2行目を-2倍して3行目に足します。
$$
\begin{pmatrix}
1 & 2 & 3\\
0 & -1 & -1\\
0 & 0 & -5
\end{pmatrix}
$$
次はどうやったら左下に0ができるでしょうか。
3行3列の-5か2行2列の-1を0にすれば良さそうですが、行基本変形でも列基本変形でも0にできそうにありません。

ルール3で2行目を-5倍して3行目に足すと3行3列が0になりますが、せっかく0にした3行2列が0じゃなくなってしまいます。こういう後退を伴うような基本変形はやらなくて大丈夫です。
ここで行き止まりになったので階段行列完成です。0以外の成分が含まれている行数は3行あるので
$$
\mathrm{rank}\, A =3
$$
です。
具体例2
$$
B
=
\begin{pmatrix}
1 & 2 & 3\\
3 & 4 & 2\\
4 & 6 & 5
\end{pmatrix}
$$
ルール3で1行目を-3倍して2行目に足し、続けて1行目を-4倍して3行目に足します。
$$
\begin{pmatrix}
1 & 2 & 3\\
0 & -2 & -7\\
0 & -2 & -7
\end{pmatrix}
$$
ルール3で2行目を-1倍して3行目に加えます。
$$
\begin{pmatrix}
1 & 2 & 3\\
0 & -2 & -7\\
0 & 0 & 0
\end{pmatrix}
$$
これで終わりです。
$$
\mathrm{rank}\, B =2
$$
です。
具体例3
$$
C
=
\begin{pmatrix}
1 & 2 & 3\\
2 & 4 & 6\\
3 & 6 & 9
\end{pmatrix}
$$
ルール3で1行目を-2倍して2行目に足し、続けて1行目を-3倍して3行目に足します。
$$
C
=
\begin{pmatrix}
1 & 2 & 3\\
0 & 0 & 0\\
0 & 0 & 0
\end{pmatrix}
$$
これで終わりです。
$$
\mathrm{rank}\, C =1
$$
です。
まとめ
行基本変形と列基本変形を使って階段行列を作ります。
階段行列の0以外の成分が含まれている行数がランクです。





コメント欄