こんにちはコーヤです。
このページでは連立1次方程式を機械的に解けるようになるクラメルの公式を勉強します。
2元連立1次方程式の場合
$$
\begin{align}
ax+by&=P
\\\\
cx+dy&=Q
\end{align}
\tag{1}
$$
この連立1次方程式を$x,y$について解くと
$$
\begin{array}{c}
x = \displaystyle \frac{Pd-bQ}{ad-bc}
\\\\
y = \displaystyle \frac{aQ-Pc}{ad-bc}
\end{array}
\tag{2}
$$
です。と言われても、これを公式として覚えるのは大変です。
そこで式(1)を行列形式に変形して
$$
\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix}
=
\begin{pmatrix}
P \\
Q
\end{pmatrix}
$$
この連立1次方程式の解は以下のように表せます。
$$
\begin{array}{c}
x
=
\displaystyle \frac
{
\begin{vmatrix}
P & b \\
Q & d
\end{vmatrix}
}
{
\begin{vmatrix}
a & b \\
c & d
\end{vmatrix}
}
&
y
=
\displaystyle \frac
{
\begin{vmatrix}
a & P \\
c & Q
\end{vmatrix}
}
{
\begin{vmatrix}
a & b \\
c & d
\end{vmatrix}
}
\end{array}
\tag{3}
$$
式(3)の行列式を計算すると式(2)と一致します。
式(3)の構造は画像で見ると分かりやすいです。
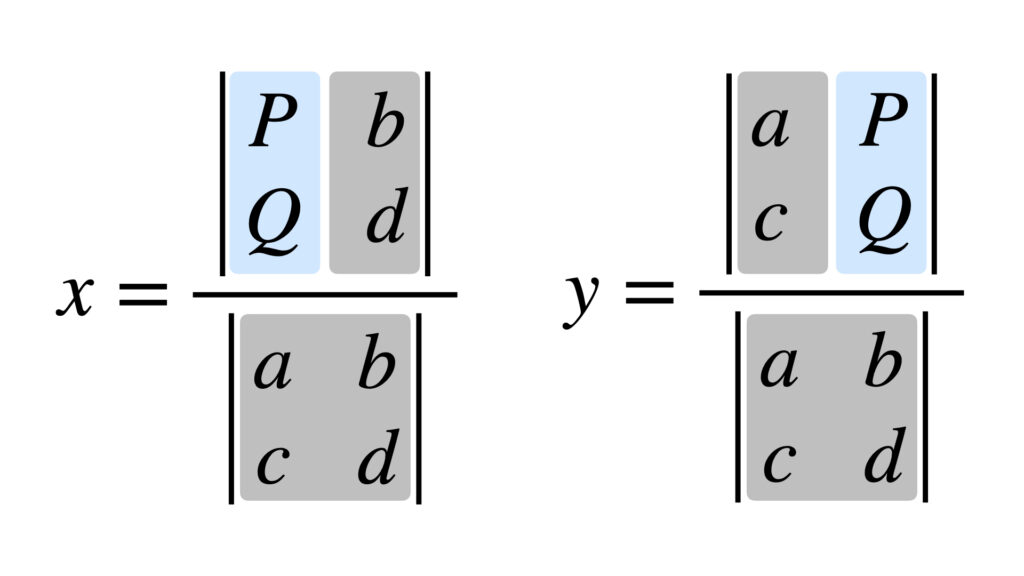
このように行列式を用いて連立1次方程式の解を表すのがクラメルの公式です。
3元連立1次方程式の場合
次は変数3つの場合を見てみましょう。2元のときと公式の使い方は同じです。
$$
\begin{align}
ax+by+cz&=P
\\\\
dx+ey+fz&=Q
\\\\
gx+hy+iz&=R
\end{align}
$$
これを行列形式に変形して
$$
\begin{pmatrix}
a & b & c \\
d & e & f \\
g & h & i
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
z
\end{pmatrix}
=
\begin{pmatrix}
P \\
Q \\
R
\end{pmatrix}
$$
この連立1次方程式の解は以下のように表せます。
$$
\begin{array}{c}
x
=
\displaystyle \frac
{
\begin{vmatrix}
P & b & c \\
Q & e & f \\
R & h & i
\end{vmatrix}
}
{
\begin{vmatrix}
a & b & c \\
d & e & f \\
g & h & i
\end{vmatrix}
}
&
y
=
\displaystyle \frac
{
\begin{vmatrix}
a & P & c \\
d & Q & f \\
g & R & i
\end{vmatrix}
}
{
\begin{vmatrix}
a & b & c \\
d & e & f \\
g & h & i
\end{vmatrix}
}
&
z
=
\displaystyle \frac
{
\begin{vmatrix}
a & b & P \\
d & e & Q \\
g & h & R
\end{vmatrix}
}
{
\begin{vmatrix}
a & b & c \\
d & e & f \\
g & h & i
\end{vmatrix}
}
\end{array}
$$
2元のときと同じような行列式の構造になっています。
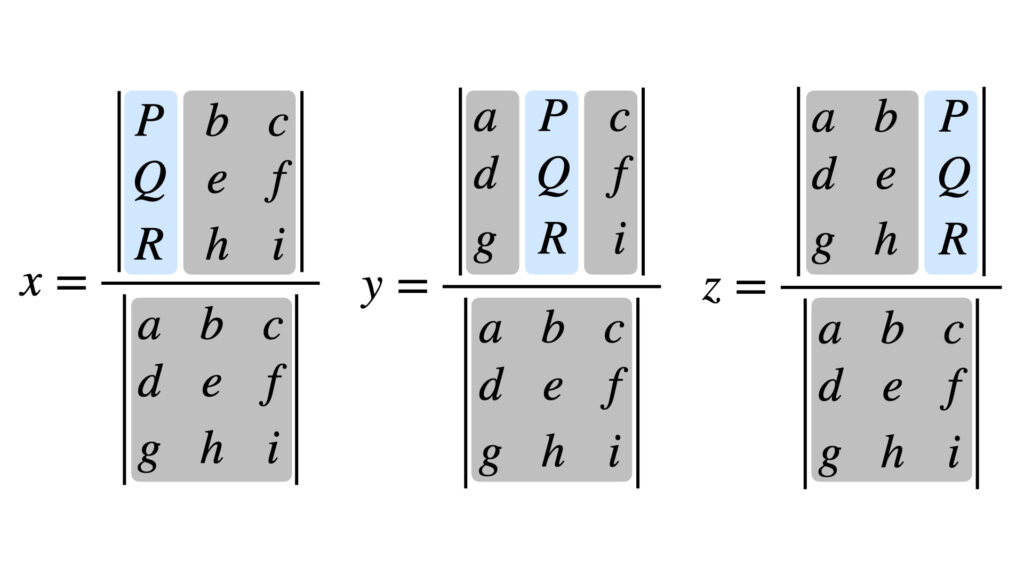
クラメルの公式の具体例
それでは具体例2つでクラメルの公式を使う練習をしましょう。
具体例1
$$
\begin{align}
x+2y+3z&=25
\\\\
3x+4y+2z&=41
\\\\
2x+3y+5z&=43
\end{align}
$$
これを行列形式に変形して
$$
\begin{pmatrix}
1 & 2 & 3 \\
3 & 4 & 2 \\
2 & 3 & 5
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
z
\end{pmatrix}
=
\begin{pmatrix}
25 \\
41 \\
43
\end{pmatrix}
$$
これをクラメルの公式で解きます。
$$
x
=
\displaystyle \frac
{
\begin{vmatrix}
25 & 2 & 3 \\
41 & 4 & 2 \\
43 & 3 & 5
\end{vmatrix}
}
{
\begin{vmatrix}
1 & 2 & 3 \\
3 & 4 & 2 \\
2 & 3 & 5
\end{vmatrix}
}
=
\frac{-35}{-5}
=
7
$$
$$
y
=
\displaystyle \frac
{
\begin{vmatrix}
1 & 25 & 3 \\
3 & 41 & 2 \\
2 & 43 & 5
\end{vmatrix}
}
{
\begin{vmatrix}
1 & 2 & 3 \\
3 & 4 & 2 \\
2 & 3 & 5
\end{vmatrix}
}
=
\frac{-15}{-5}
=
3
$$
$$
z
=
\displaystyle \frac
{
\begin{vmatrix}
1 & 2 & 25 \\
3 & 4 & 41 \\
2 & 3 & 43
\end{vmatrix}
}
{
\begin{vmatrix}
1 & 2 & 3 \\
3 & 4 & 2 \\
2 & 3 & 5
\end{vmatrix}
}
=
\frac{-20}{-5}
=
4
$$
具体例2
上の例の3つ目の式を変えました。
$$
\begin{align}
x+2y+3z&=25
\\\\
3x+4y+2z&=41
\\\\
4x+6y+5z&=66
\end{align}
$$
これを行列形式に変形して
$$
\begin{pmatrix}
1 & 2 & 3 \\
3 & 4 & 2 \\
4 & 6 & 5
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
z
\end{pmatrix}
=
\begin{pmatrix}
25 \\
41 \\
66
\end{pmatrix}
$$
これをクラメルの公式で解きます。
$$
x
=
\displaystyle \frac
{
\begin{vmatrix}
25 & 2 & 3 \\
41 & 4 & 2 \\
66 & 6 & 5
\end{vmatrix}
}
{
\begin{vmatrix}
1 & 2 & 3 \\
3 & 4 & 2 \\
4 & 6 & 5
\end{vmatrix}
}
=
\frac{0}{0}
$$
怪しい解になってしまいました。分母が0になる場合はクラメルの公式は使えません。
クラメルの公式が使えない連立1次方程式を解くときは、自由度の知識が必要になります。
まとめ
クラメルの公式は分母は係数行列、分子は係数行列の列を解で置き換えて行列式を求めます。






コメント欄