こんにちはコーヤです。
このページでは行列の重要な値である行列式の計算方法を2次、3次、4次以降と順に勉強します。
2次の行列式
まずは2次の行列式から見ていきます。
$$
A
=
\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}
$$
このとき行列式は以下のとおりです。
$$
\det A
=
ad-bc
$$
行列式はこのように$\det$を使って表す場合と、行列を囲んでいるかっこを縦棒にして表す場合があります。
$$
\begin{vmatrix}
a & b \\
c & d
\end{vmatrix}
=
ad-bc
$$
意味は同じです。どちらもよく使う表記なので知っておきましょう。
3次の行列式
次は3次の行列式です。2次の時よりちょっと複雑になります。
$$
A
=
\begin{pmatrix}
a & b & c\\
d & e & f\\
g & h & i
\end{pmatrix}
$$
このとき行列式は
$$
\det A
=
aei+bfg+cdh-ceg-bdi-afh
$$
です。サラスの公式という名前がついています。
この式の覚え方は「↘︎成分−↙︎成分」です。
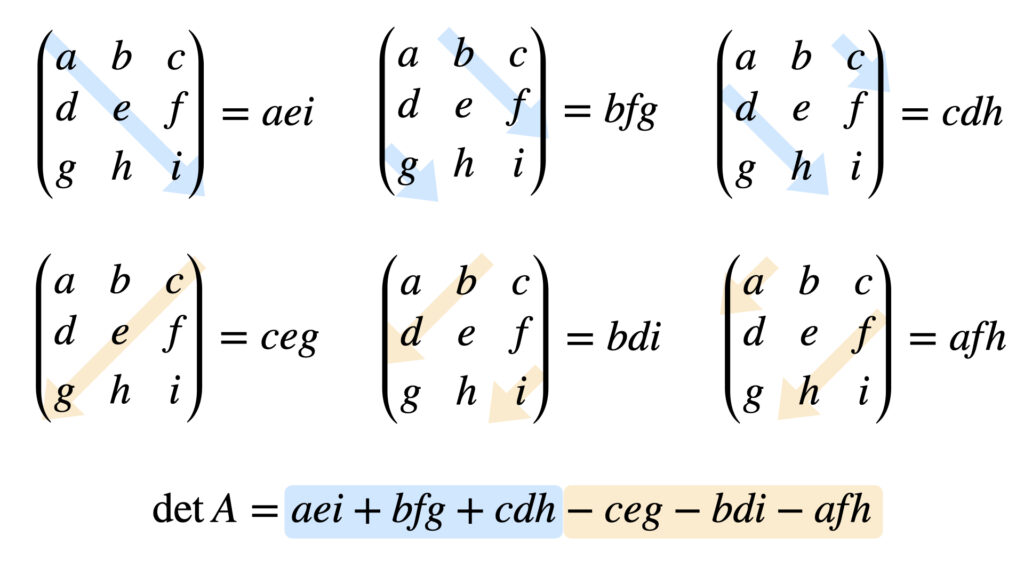
2次の行列式も「↘︎成分−↙︎成分」になっています。
4次以降の行列式
4次以降の行列式は「↘︎成分−↙︎成分」では求まりません。余因子展開を使って求めましょう。
余因子展開の計算方法は余因子展開のページをご覧ください。
行列式計算の具体例
それでは具体例4つで行列式の公式を使う練習をしましょう。
具体例1
$$
\begin{vmatrix}
3 & 2 \\
5 & 4
\end{vmatrix}
$$
公式に当てはめるだけです。
$$
\begin{align}
\begin{vmatrix}
3 & 2 \\
5 & 4
\end{vmatrix}
&=
3 \cdot 4-2 \cdot 5
\\\\&=
2
\end{align}
$$
具体例2
$$
\begin{vmatrix}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{vmatrix}
$$
変数があっても公式の使い方は変わりません。
$$
\begin{align}
\begin{vmatrix}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{vmatrix}
&=
\cos^2 \theta-(-\sin^2 \theta)
\\\\&=
1
\end{align}
$$
具体例3
$$
\begin{vmatrix}
1 & 2 & 3\\
4 & 5 & 6\\
7 & 8 & 9
\end{vmatrix}
$$
これも公式に当てはめるだけです。
「↘︎成分−↙︎成分」です。矢印の方向を間違えないように注意しましょう。
$$
\begin{align}
\begin{vmatrix}
1 & 2 & 3\\
4 & 5 & 6\\
7 & 8 & 9
\end{vmatrix}
&=
1 \cdot 5 \cdot 9
+2 \cdot 6 \cdot 7
+3 \cdot 4 \cdot 8
-3 \cdot 5 \cdot 7
-2 \cdot 4 \cdot 9
-1 \cdot 6 \cdot 8
\\\\&=
45+84+96-105-72-48
\\\\&=
0
\end{align}
$$
具体例4
$$
\begin{vmatrix}
1 & 1 & 1\\
x & y & z\\
yz & zx & xy
\end{vmatrix}
$$
変数があっても公式の使い方は変わりません。
$$
\begin{align}
\begin{vmatrix}
1 & 1 & 1\\
x & y & z\\
yz & zx & xy
\end{vmatrix}
&=
xy^2+yz^2+zx^2-y^2z-x^2y-z^2x
\\\\&=
(x-y)(y-z)(z-x)
\end{align}
$$
行列式に変数が含まれたままの場合は因数分解しておくのがポイントです。
行列式の値が0かどうかで場合分けすることが多いので、因数分解してある形のほうが0になる条件が判断しやすくなります。
まとめ
2次、3次の行列式は「↘︎成分−↙︎成分」で求めます。
4次以降の行列式は余因子展開で求めます。
コメント欄