こんにちはコーヤです。
このページでは、二変数関数の積分である重積分の意味と計算方法を勉強します。
積分と重積分の違い
積分と比べながら重積分の意味を確認します。
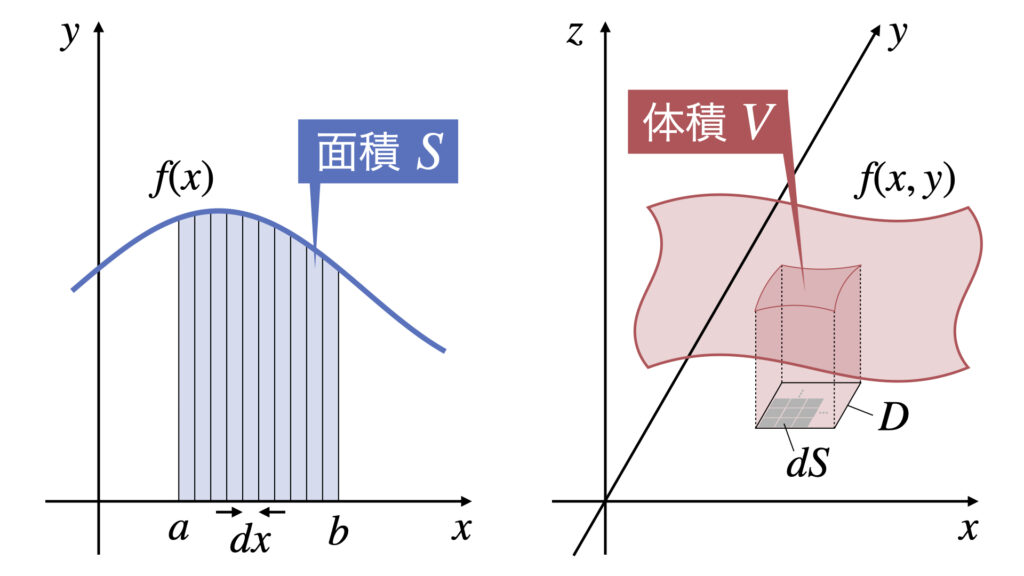
積分の意味
微小区間$dx$で区切られる長方形の面積の和から、積分範囲$(a,b)$の面積$S$を求めることができます。
$$
S
=
\displaystyle\int_a^b
f(x)
~dx
$$
重積分の意味
微小区間$dS$で作られる直方体の体積の和から、積分領域$D$の体積$V$を求めることができます。
$$
V
=
\displaystyle\iint_D
f(x,y)
~dS
$$
$dS$は面積要素や面素と呼びます。
$dS$は$x$軸方向の微小区間$dx$と$y$軸方向の微小区間$dy$の積で表すことができます。
$$
dS=dxdy
$$
重積分の計算方法
前述の通り重積分の意味は直方体の和ですが、計算の流れは以下の2ステップで行われます。
- 断面積を求める
- 断面積を積分して体積を求める
それでは例題で重積分の計算をしてみましょう。
以下の体積を求めます。
$$
\begin{array}{ll}
f(x,y)=x+y
\\\\
D=\{(x,y) ~|~ 1 \leqq x \leqq 2, 0 \leqq y \leqq 1\}
\end{array}
$$
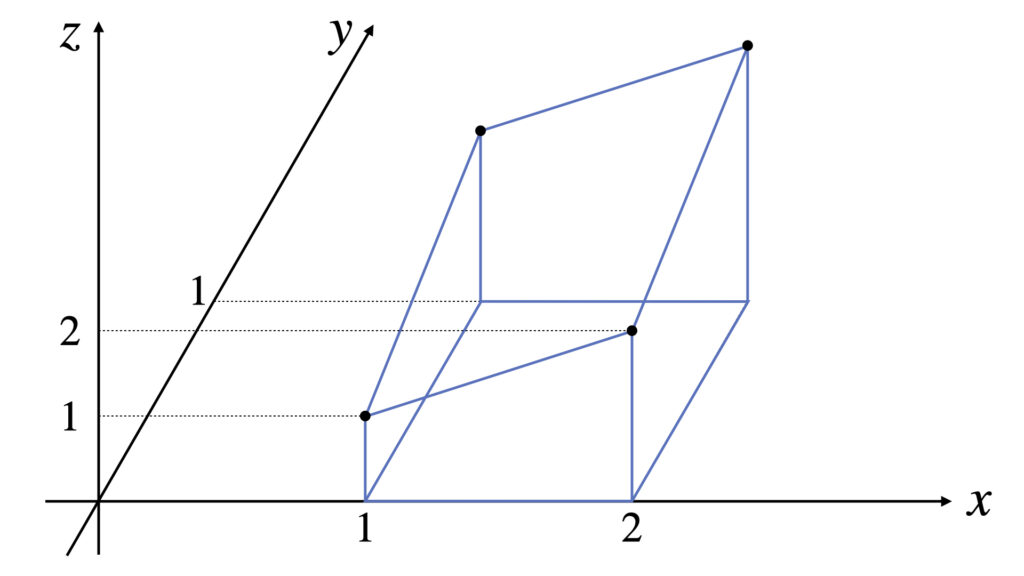
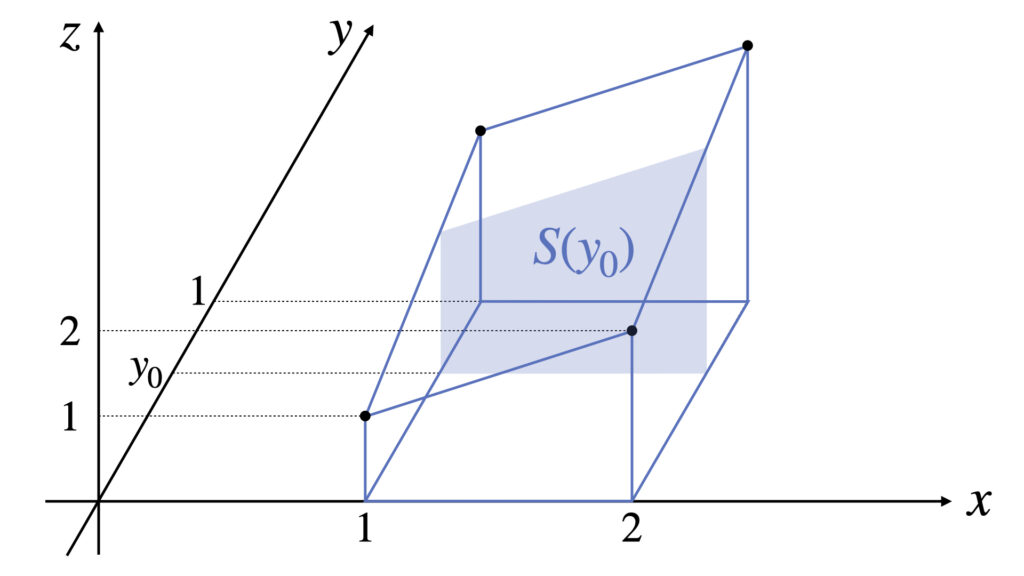
まずは$y=y_0$と固定して、断面積$S(y_0)$を求めます。
$$
\begin{align}
S(y_0)
&=
\displaystyle\int_1^2
f(x, y_0)
~dx
\\\\&=
\displaystyle\int_1^2
x+y_0
~dx
\\\\&=
\left[
\displaystyle\frac{1}{2}x^2+xy_0
\right]_1^2
\\\\&=
\displaystyle\frac{3}{2}+y_0
\end{align}
$$
$y_0$を変数$y$に戻して、断面積$S(y)$を積分して体積$V$を求めます。
$$
\begin{align}
V
&=
\displaystyle\int_0^1
S(y)
~dy
\\\\&=
\displaystyle\int_0^1
\displaystyle\frac{3}{2}+y
~dy
\\\\&=
\left[
\displaystyle\frac{3}{2}y+\displaystyle\frac{1}{2}y^2
\right]_0^1
\\\\&=
2
\end{align}
$$
これで体積$V$が求まりました。
今回は$y$を固定して計算しましたが、$x$を固定しても結果は変わりません。
$x=x_0$と固定するパターンも計算してみます。断面積$S(x_0)$を求めます。
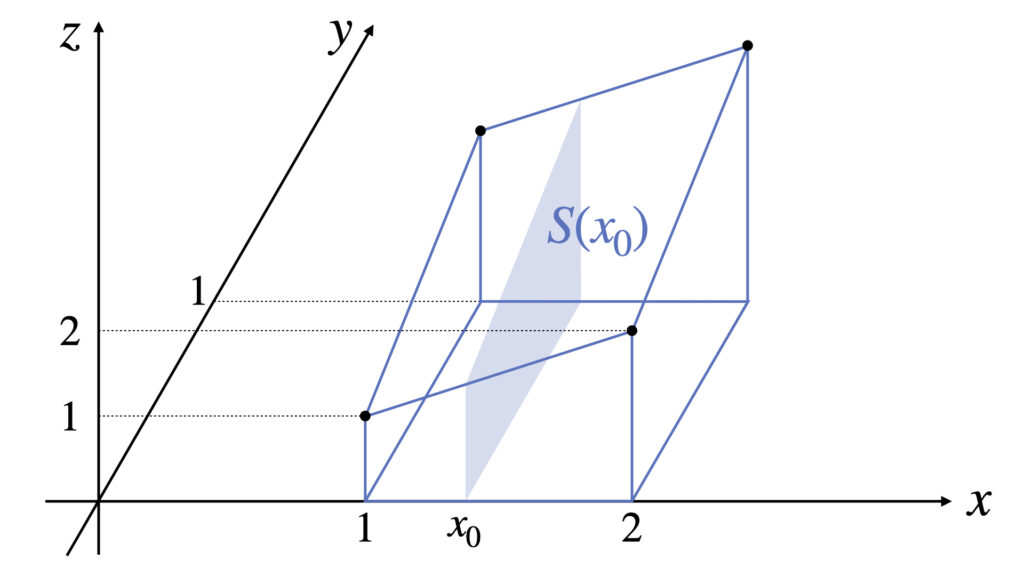
$$
\begin{align}
S(x_0)
&=
\displaystyle\int_0^1
f(x_0, y)
~dy
\\\\&=
\displaystyle\int_0^1
x_0+y
~dy
\\\\&=
\left[
x_0y+\displaystyle\frac{1}{2}y^2
\right]_0^1
\\\\&=
x_0+\displaystyle\frac{1}{2}
\end{align}
$$
$x_0$を変数$x$に戻して、断面積$S(x)$を積分して体積$V$を求めます。
$$
\begin{align}
V
&=
\displaystyle\int_1^2
S(x)
~dx
\\\\&=
\displaystyle\int_1^2
x+\displaystyle\frac{1}{2}
~dx
\\\\&=
\left[
\displaystyle\frac{1}{2}x^2+\displaystyle\frac{1}{2}x
\right]_1^2
\\\\&=
2
\end{align}
$$
このように、重積分はどちらの変数から積分しても結果は変わりません。
慣れてきたら断面積を経由せずに計算してみましょう。
$$
\begin{align}
V
&=
\displaystyle\iint_D
f(x, y)
~dS
\\\\&=
\displaystyle\iint_D
x+y
~dS
\\\\&=
\displaystyle\int_0^1
\displaystyle\int_1^2
x+y
~dxdy
\\\\&=
\displaystyle\int_0^1
\left(
\displaystyle\int_1^2
x+y
~dx
\right)
~dy
\\\\&=
\displaystyle\int_0^1
\left(
\left[
\displaystyle\frac{1}{2}x^2+xy
\right]_1^2
\right)
~dy
\\\\&=
\displaystyle\int_0^1
\left(
\displaystyle\frac{3}{2}+y
\right)
~dy
\\\\&=
\displaystyle\int_0^1
\displaystyle\frac{3}{2}+y
~dy
\\\\&=
\left[
\displaystyle\frac{3}{2}y+\displaystyle\frac{1}{2}y^2
\right]_0^1
\\\\&=
2
\end{align}
$$
このように$x$で積分するときは$y$を定数扱いしてあげればOKです。

変数を定数扱いするのは、偏微分の計算と同じイメージです。
変数分離できる場合の計算方法
$$
f(x, y)=g(x)h(y)
$$
のように変数分離できる場合は、以下のように別々の積分にすることができます。
$$
\displaystyle\iint_D
f(x, y)
~dS
=
\displaystyle\int
g(x)
~dx
\displaystyle\int
h(y)
~dy
$$
それでは例題で変数分離の重積分を計算をしてみましょう。
$$
\begin{array}{ll}
f(x,y)=xy
\\\\
D=\{(x,y) ~|~ 1 \leqq x \leqq 2, 0 \leqq y \leqq 1\}
\end{array}
$$
これを$x$から積分する場合、$y$から積分する場合、変数分離する場合の3パターンで計算します。
$x$から積分する場合
$$
\begin{align}
V
&=
\displaystyle\iint_D
xy
~dS
\\\\&=
\displaystyle\int_0^1
\displaystyle\int_1^2
xy
~dxdy
\\\\&=
\displaystyle\int_0^1
\left[
\displaystyle\frac{1}{2}x^2y
\right]_1^2
~dy
\\\\&=
\displaystyle\int_0^1
\displaystyle\frac{3}{2}y
~dy
\\\\&=
\left[
\displaystyle\frac{3}{4}y^2
\right]_0^1
\\\\&=
\displaystyle\frac{3}{4}
\end{align}
$$
$y$から積分する場合
$$
\begin{align}
V
&=
\displaystyle\iint_D
xy
~dS
\\\\&=
\displaystyle\int_1^2
\displaystyle\int_0^1
xy
~dydx
\\\\&=
\displaystyle\int_1^2
\left[
\displaystyle\frac{1}{2}xy^2
\right]_0^1
~dx
\\\\&=
\displaystyle\int_1^2
\displaystyle\frac{1}{2}x
~dx
\\\\&=
\left[
\displaystyle\frac{1}{4}x^2
\right]_1^2
\\\\&=
\displaystyle\frac{3}{4}
\end{align}
$$
変数分離する場合
$$
\begin{align}
V
&=
\displaystyle\iint_D
xy
~dS
\\\\&=
\displaystyle\int_1^2
x
~dx
\displaystyle\int_0^1
y
~dy
\\\\&=
\left[
\displaystyle\frac{1}{2}x^2
\right]_1^2
\cdot
\left[
\displaystyle\frac{1}{2}y^2
\right]_0^1
\\\\&=
\displaystyle\frac{3}{2}
\cdot
\displaystyle\frac{1}{2}
\\\\&=
\displaystyle\frac{3}{4}
\end{align}
$$
どの方法で計算してもOKです。
積分領域が変数の場合の計算方法
積分領域$D$が$xy$の関数で定義されるときは、積分範囲に注意が必要です。
例題として、以下の積分領域$D$で$f(x,y)=x+y$を積分します。
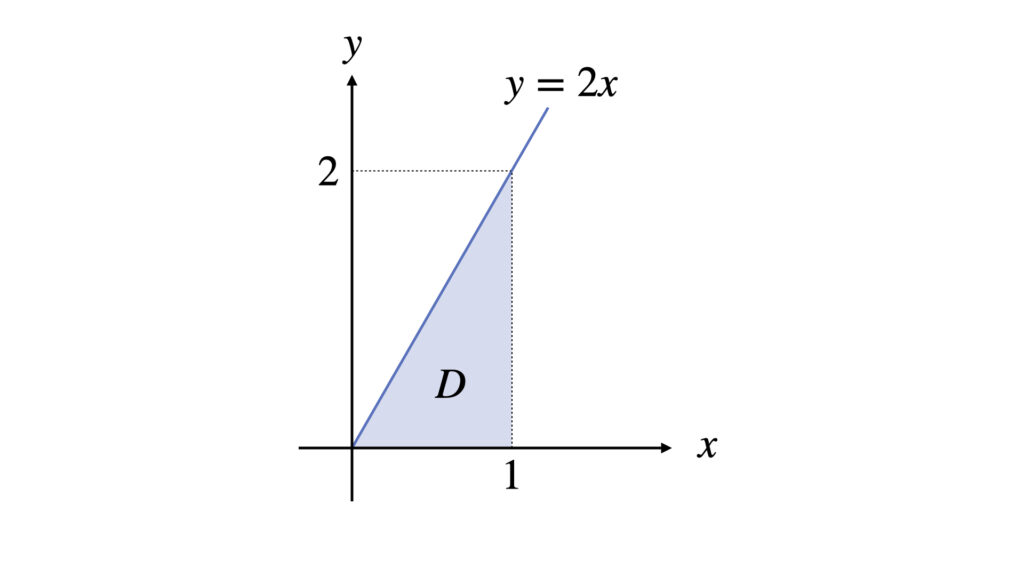
このように積分領域に変数が含まれる場合、どちらかの変数の積分範囲をもう一方の変数で表します。
$y$の積分範囲を$x$で表す場合
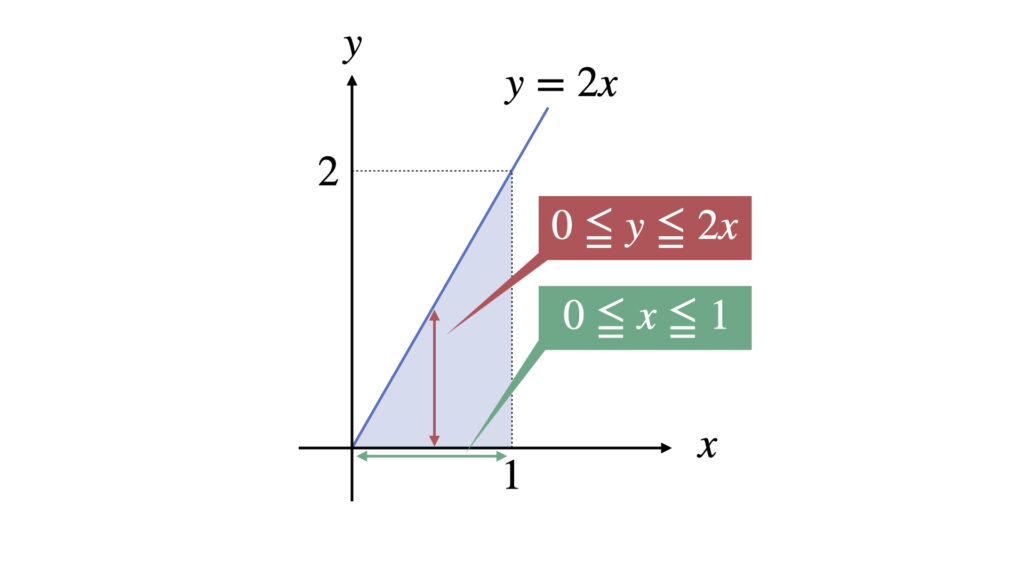
$y$の積分範囲を$x$で表した場合は、$y$の積分を先に行います。
$$
\begin{align}
V
&=
\displaystyle\iint_D
x+y
~dS
\\\\&=
\displaystyle\int_0^1
\displaystyle\int_1^{2x}
x+y
~dydx
\\\\&=
\displaystyle\int_0^1
\left[
xy+\displaystyle\frac{1}{2}y^2
\right]_1^{2x}
~dx
\\\\&=
\displaystyle\int_0^1
4x^2
~dx
\\\\&=
\left[
\displaystyle\frac{4}{3}x^3
\right]_0^1
\\\\&=
\displaystyle\frac{4}{3}
\end{align}
$$
$x$の積分範囲を$y$で表す場合
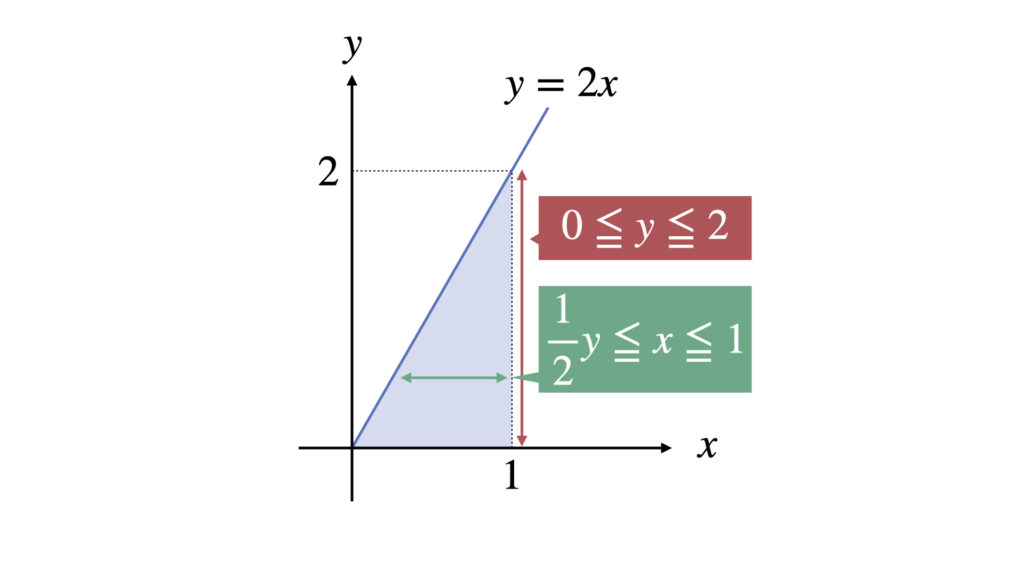
$x$の積分範囲を$y$で表した場合は、$x$の積分を先に行います。
$$
\begin{align}
V
&=
\displaystyle\iint_D
x+y
~dS
\\\\&=
\displaystyle\int_0^2
\displaystyle\int_{\frac{1}{2}y}^1
x+y
~dxdy
\\\\&=
\displaystyle\int_0^2
\left[
\displaystyle\frac{1}{2}x^2+xy
\right]_{\frac{1}{2}y}^1
~dy
\\\\&=
\displaystyle\int_0^2
-\displaystyle\frac{5}{8}y^2+y+\displaystyle\frac{1}{2}
~dy
\\\\&=
\left[
-\displaystyle\frac{5}{24}y^3+\displaystyle\frac{1}{2}y^2+\displaystyle\frac{1}{2}y
\right]_0^2
\\\\&=
\displaystyle\frac{4}{3}
\end{align}
$$
積分の順番を変更する場合の計算方法
以下の重積分を求めます。
$$
\begin{array}{ll}
f(x,y)=\sin x \sin^\alpha y ~~~(0< \alpha)
\\\\
D=\{(x,y) ~|~ 0 \leqq x \leqq \displaystyle\frac{1}{2}\pi, 0 \leqq y \leqq x\}
\end{array}
$$
これは$y$の積分範囲に$x$が含まれているので、先に$y$を積分します。
$$
\begin{align}
V
&=
\displaystyle\iint_D
\sin x \sin^\alpha y
~dS
\\\\&=
\displaystyle\int_0^{\frac{1}{2}\pi}
\displaystyle\int_0^x
\sin x \sin^\alpha y
~dydx
\end{align}
$$
このように式を立てると$\sin^\alpha y$の積分でストップします。
このとき、積分領域$D$の表現方法を変えることで重積分がスムーズにできるときがあります。
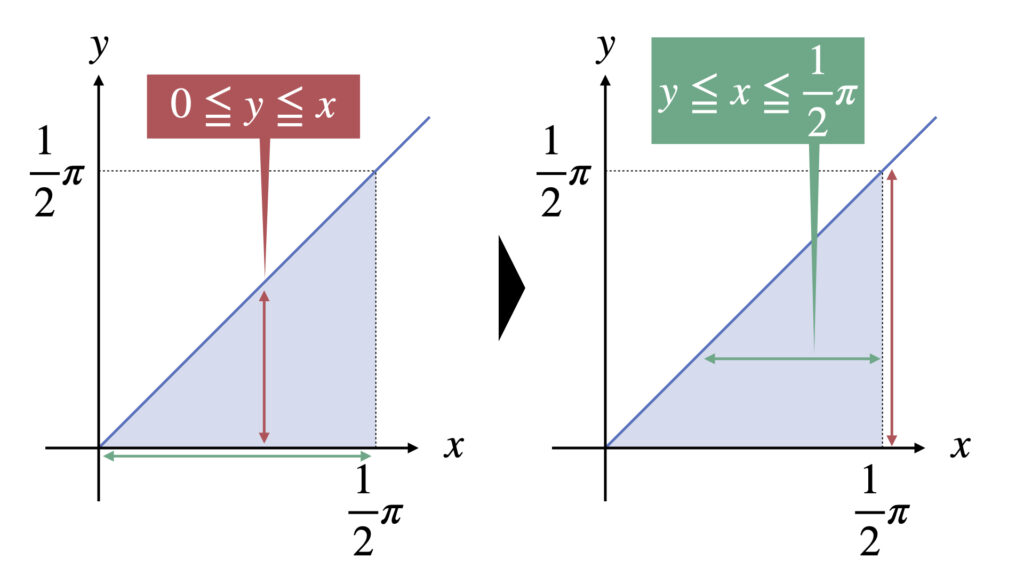
上図左側では$y$の積分範囲に$x$が含まれていますが、右側のように$x$の積分範囲に$y$が含まれる形に変更します。
すると重積分の計算は以下のようになります。
$$
\begin{align}
V
&=
\displaystyle\iint_D
\sin x \sin^\alpha y
~dS
\\\\&=
\displaystyle\int_0^{\frac{1}{2}\pi}
\displaystyle\int_y^{\frac{1}{2}\pi}
\sin x \sin^\alpha y
~dxdy
\\\\&=
\displaystyle\int_0^{\frac{1}{2}\pi}
\left[
-\cos x \sin^\alpha y
\right]_y^{\frac{1}{2}\pi}
~dy
\\\\&=
\displaystyle\int_0^{\frac{1}{2}\pi}
\cos y \sin^\alpha y
~dy
\end{align}
$$
ここで置換積分を行います。
$$
\begin{align}
t&=\sin y
\\\\
dt&=\cos y
\end{align}
$$
$$
\begin{array}{ccccc}
y & : & 0 & \to & \displaystyle\frac{1}{2}\pi
\\\\
t & : & 0 & \to & 1
\end{array}
$$
$$
\begin{align}
V
&=
\displaystyle\int_0^{\frac{1}{2}\pi}
\cos y \sin^\alpha y
~dy
\\\\&=
\displaystyle\int_0^1
t^\alpha
~dt
\\\\&=
\left[
\displaystyle\frac{1}{\alpha +1}t^{\alpha +1}
\right]_0^1
\\\\&=
\displaystyle\frac{1}{\alpha +1}
\end{align}
$$
このように簡単に積分することができました。
まとめ
重積分は微小区間$dS$で積分領域$D$を積分します。計算方法は1つの変数に注目した積分を2回行います。
$$
V
=
\displaystyle\iint_D
f(x,y)
~dS
$$




コメント欄