こんにちはコーヤです。
このページでは、テイラー展開の収束半径の勉強をします。収束半径が分かるとテイラー展開が使える範囲と使えない範囲が判断できます。
収束半径の概要
テイラー展開は$x=a$付近での関数を級数で表現する方法でしたが、「付近」とはどのくらいの範囲なのかを明確にしよう、という主旨です。
「付近」とみなせる範囲のことを収束半径といいます。
関数によって収束半径が異なるので、テイラー展開をするときは一緒に収束半径も計算しないといけません。
収束半径の計算方法
テイラー展開の公式は以下の式でした。
$$
f(x)
=
\displaystyle\sum_{n=0}^\infty
\displaystyle\frac{1}{n!}
f^{(n)}(a)(x-a)^n
$$
シグマを展開して、以下のように係数$c_n$を決めます。
$$
\displaystyle\sum_{n=0}^\infty
\displaystyle\frac{1}{n!}
f^{(n)}(a)(x-a)^n
=
c_0+c_1x+c_2x^2+c_3x^3+\cdots+c_nx^n+\cdots
$$
このように足し算が無限に続くので、右辺は無限級数と捉えることができます。
この無限級数が収束するかどうか、ダランベールの収束判定法で計算してみましょう。
ダランベールの収束判定法の詳細は収束判定法のページをご覧ください。
$$
\begin{align}
r
&=
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{\left|c_{n+1}x^{n+1}\right|}{\left|c_nx^n\right|}
\\\\&=
\displaystyle\lim_{n \to \infty}
\left|\displaystyle\frac{c_{n+1}}{c_n}\right||x|
\end{align}
$$
これが収束するか発散するかは$r=1$のときが境目なので、$r=1$を満たす$|x|$を$|x|=R$とします。
$$
\displaystyle\lim_{n \to \infty}
\left|
\displaystyle\frac{c_{n+1}}{c_n}
\right|
R
=
1
$$
これより
$$
R
=
\displaystyle\lim_{n \to \infty}
\left|
\displaystyle\frac{c_n}{c_{n+1}}
\right|
$$
となります。この$R$の値を用いて
- $|x|<R$ならテイラー展開は収束
- $|x|>R$ならテイラー展開は発散
- $|x|=R$のテイラー展開は個別調査が必要
と無限級数の収束判定ができます。この$R$を収束半径といい、テイラー展開できるのは$|x|<R$の範囲だけです。

無限級数が収束するような$x$の範囲のことを「付近」とみなしていた、ということです。
収束半径が無限の場合
$f(x)=\sin x$をマクローリン展開して、収束半径を求めましょう。
まずはマクローリン展開から計算します。
$$
\begin{align}
\sin x
&=
x-\displaystyle\frac{1}{6}x^3+\displaystyle\frac{1}{120}x^5-\displaystyle\frac{1}{5040}x^7+\cdots
\\\\&=
\displaystyle\sum_{n=0}^\infty
\displaystyle\frac{(-1)^n}{(2n+1)!}
x^{2n+1}
\end{align}
$$
シグマの形でマクローリン展開を表せたので、収束半径$R$の計算をします。
$$
\begin{align}
R
&=
\displaystyle\lim_{n \to \infty}
\left|
\displaystyle\frac{c_n}{c_{n+1}}
\right|
\\\\&=
\displaystyle\lim_{n \to \infty}
\left|
\displaystyle\frac
{\displaystyle\frac{(-1)^n}{(2n+1)!}}
{\displaystyle\frac{(-1)^{n+1}}{(2n+3)!}}
\right|
\\\\&=
\displaystyle\lim_{n \to \infty}
(2n+3)(2n+2)
\\\\&=
\infty
\end{align}
$$
収束半径は$R=\infty$となりました。つまり$\sin x$のマクローリン展開は$|x|<\infty$の範囲で展開できるということです。$|x|<\infty$の範囲は$x$軸全体です。
3次式の近似から15次式の近似までを表示するGIF画像です。
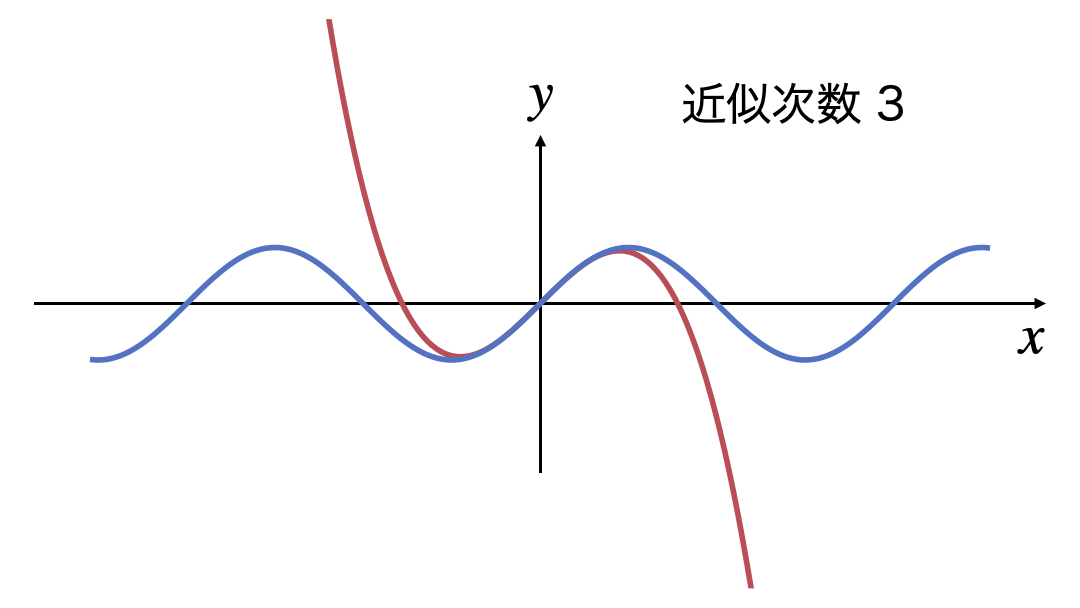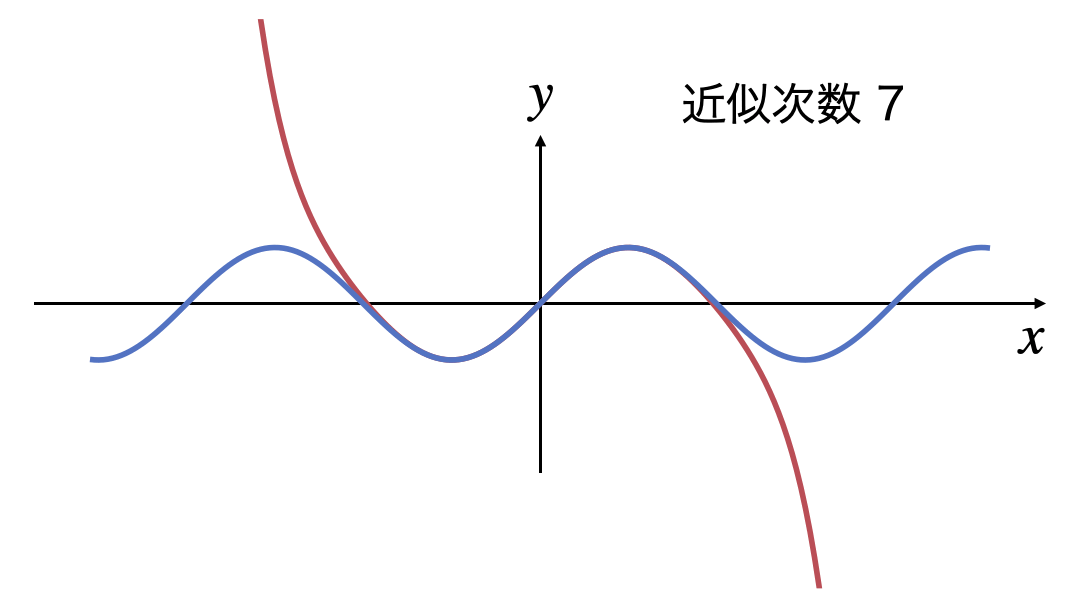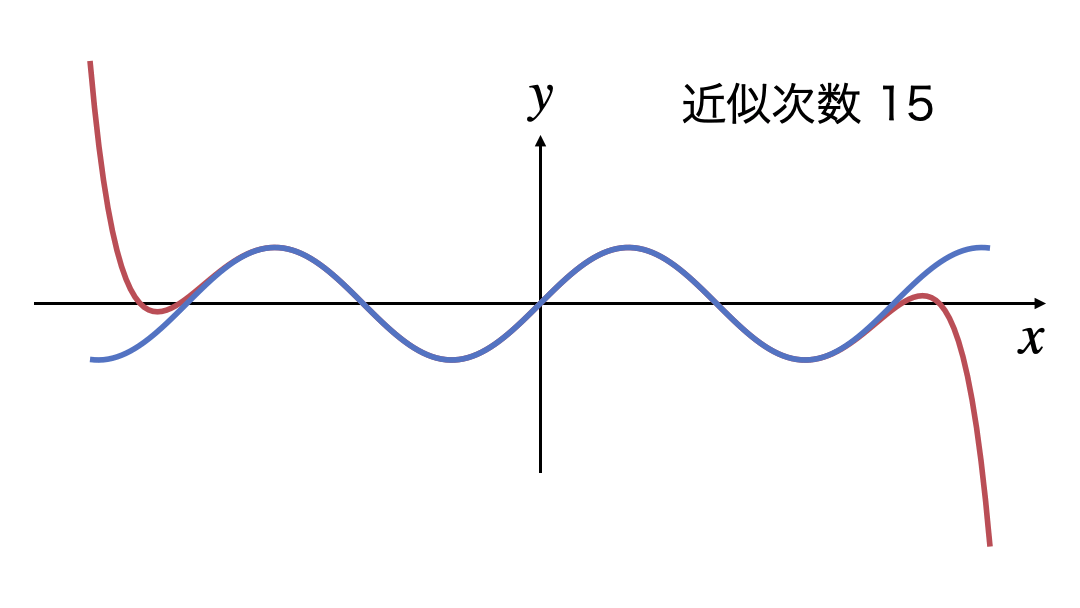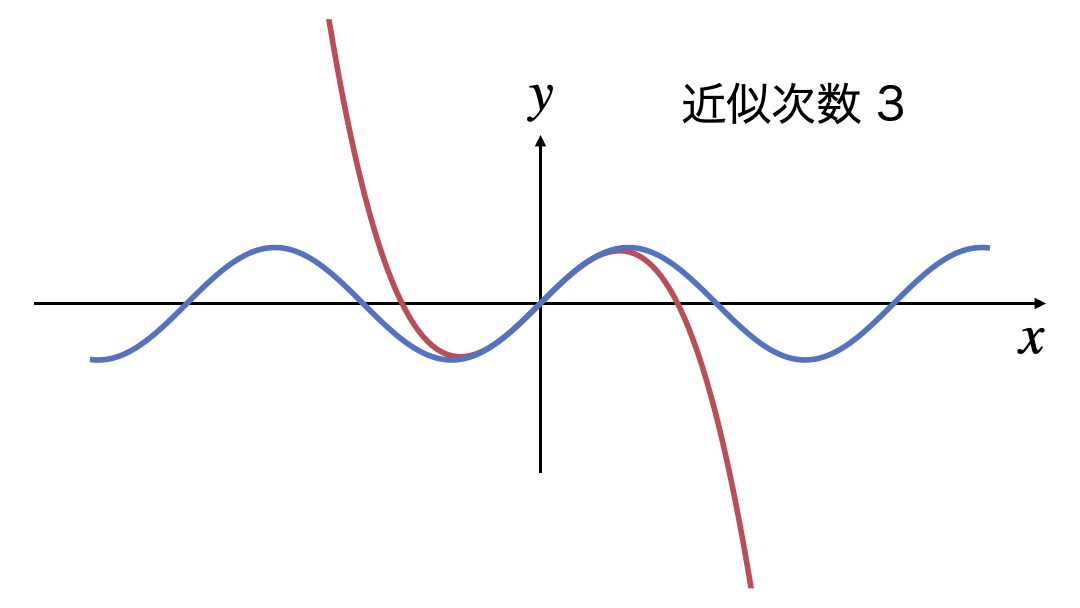
次数を上げていけば近似できる$x$の範囲がどんどん広がっていき、$x$軸全体になりそう感じが読み取れます。
収束半径が有限の場合
$f(x)=\log(1+x)$をマクローリン展開して、収束半径を求めましょう。
まずはマクローリン展開から計算します。
$$
\begin{align}
\log(1+x)
&=
x-\displaystyle\frac{1}{2}x^2+\displaystyle\frac{1}{3}x^3-\displaystyle\frac{1}{4}x^4+\cdots
\\\\&=
\displaystyle\sum_{n=0}^\infty
\displaystyle\frac{(-1)^n}{n+1}
x^{n+1}
\end{align}
$$
シグマの形でマクローリン展開を表せたので、収束半径$R$の計算をします。
$$
\begin{align}
R
&=
\displaystyle\lim_{n \to \infty}
\left|
\displaystyle\frac{c_n}{c_{n+1}}
\right|
\\\\&=
\displaystyle\lim_{n \to \infty}
\left|
\displaystyle\frac
{\displaystyle\frac{(-1)^n}{n+1}}
{\displaystyle\frac{(-1)^{n+1}}{n+2}}
\right|
\\\\&=
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{n+2}{n+1}
\\\\&=
1
\end{align}
$$
収束半径は$R=1$となりました。つまり$\log(1+x)$のマクローリン展開は$|x|<1$の範囲で展開できるということです。
3次式の近似から15次式の近似までを表示するGIF画像です。
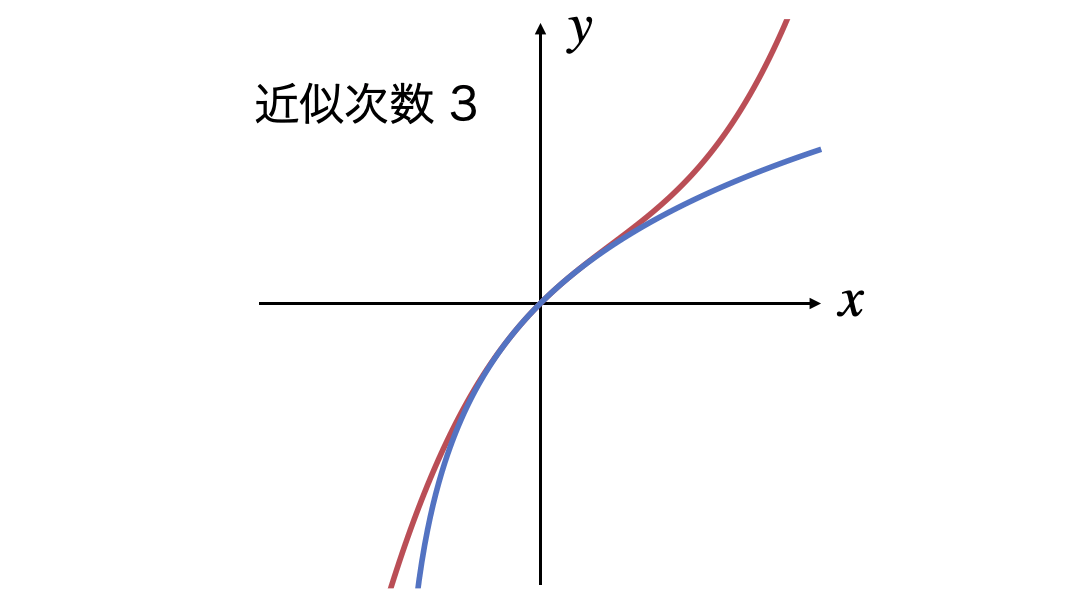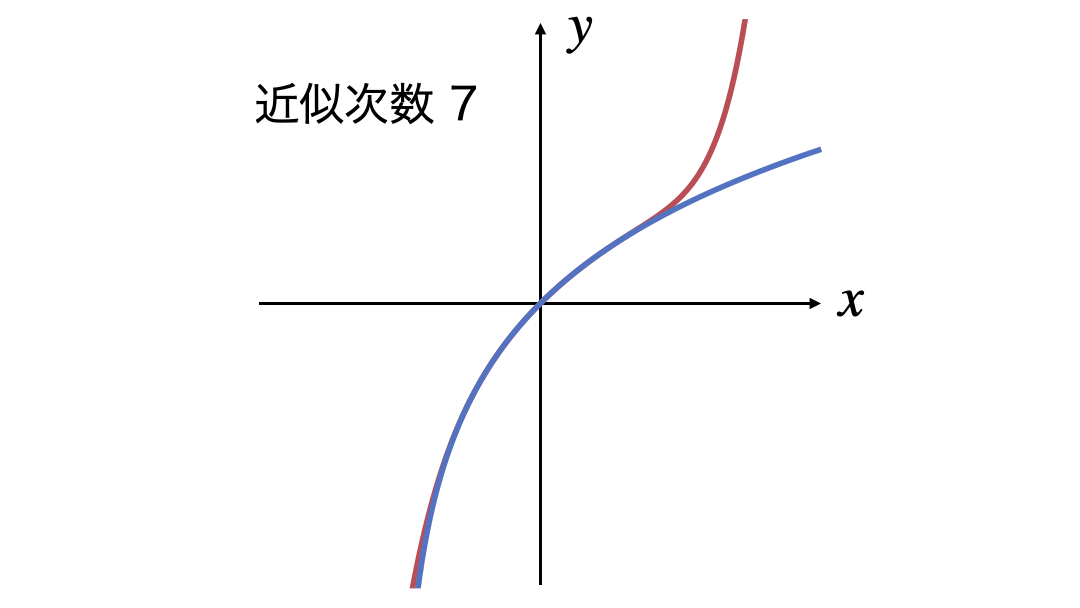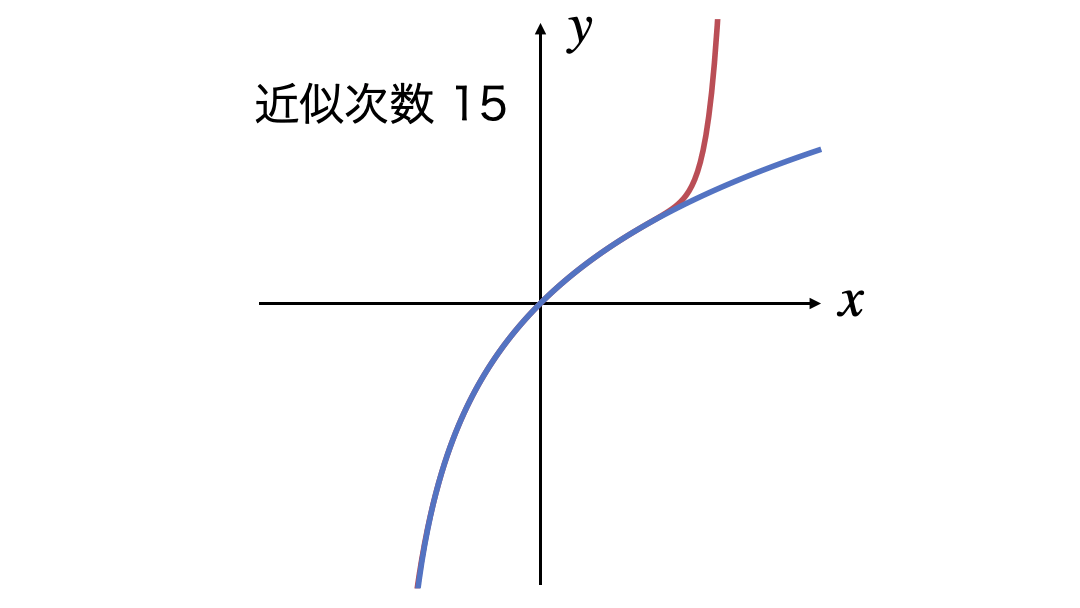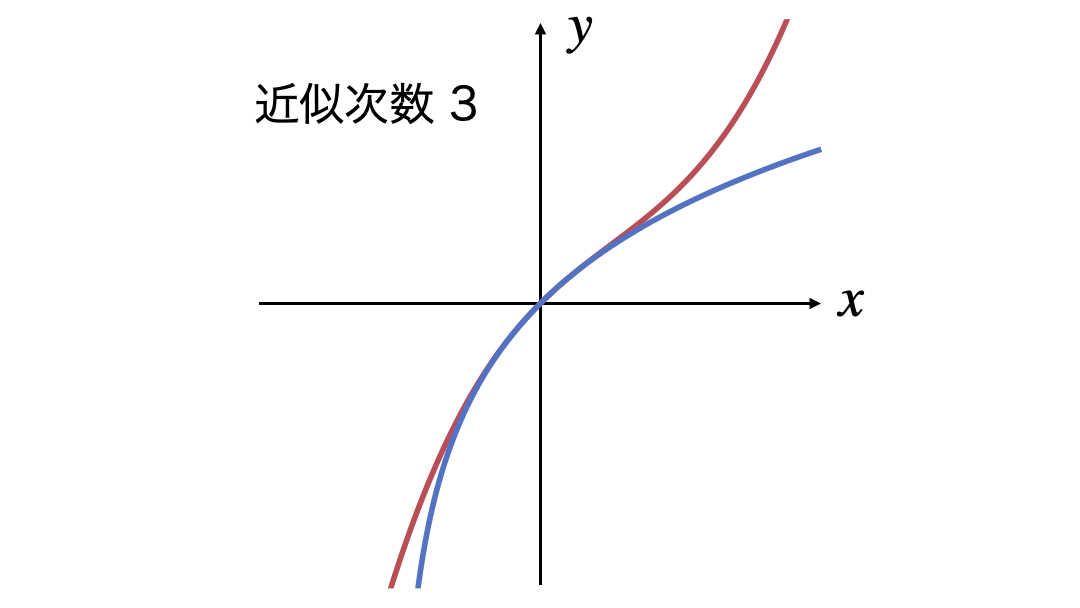
次数を上げていっても近似できる$x$の範囲が広がっていきません。収束半径が示すとおり$|x|<1$の範囲でしか近似できていなさそうです。
ここまでの計算で$|x|<1$の範囲は収束、$|x|>1$の範囲は発散であることが分かりましたが、$|x|=1$の範囲は個別調査が必要なので、$x=1$と$x=-1$がそれぞれ収束するか調べます。
$\log(1+x)$をマクローリン展開すると以下のようになっていました。
$$
\log(1+x)
=
x-\displaystyle\frac{1}{2}x^2+\displaystyle\frac{1}{3}x^3-\displaystyle\frac{1}{4}x^4+\cdots
$$
これに$x=1$と$x=-1$をそれぞれ代入して計算すると
$$
1-\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}-\displaystyle\frac{1}{4}+\cdots
=
\log 2
$$
$$-
1-\displaystyle\frac{1}{2}-\displaystyle\frac{1}{3}-\displaystyle\frac{1}{4}-\cdots
=
-\infty
$$
となり、$x=1$では収束、$x=-1$では発散となります。
この無限級数の値が$\log 2$や$-\infty$になることは収束判定法のページで計算しています。
以上より$\log(1+x)$がマクローリン展開できる範囲は$-1<x\leq 1$となります。
収束半径の代表例
以下に代表的な関数のマクローリン展開した結果と、その収束半径を示します。
$$
\begin{align}
e^x
&=
1+x+\displaystyle\frac{1}{2}x^2+\displaystyle\frac{1}{6}x^3+\cdots
\\\\&=
\displaystyle\sum_{n=0}^\infty
\displaystyle\frac{1}{n!}
x^n
~~~~(-\infty<x<\infty)
\end{align}
$$
$$
\begin{align}
\log(1+x)
&=
x-\displaystyle\frac{1}{2}x^2+\displaystyle\frac{1}{3}x^3-\displaystyle\frac{1}{4}x^4+\cdots
\\\\&=
\displaystyle\sum_{n=0}^\infty
\displaystyle\frac{(-1)^n}{n+1}
x^{n+1}
~~~~(-1<x\leq 1)
\end{align}
$$
$$
\begin{align}
\sin x
&=
x-\displaystyle\frac{1}{6}x^3+\displaystyle\frac{1}{120}x^5-\displaystyle\frac{1}{5040}x^7+\cdots
\\\\&=
\displaystyle\sum_{n=0}^\infty
\displaystyle\frac{(-1)^n}{(2n+1)!}
x^{2n+1}
~~~~(-\infty<x<\infty)
\end{align}
$$
$$
\begin{align}
\cos x
&=
1-\displaystyle\frac{1}{2}x^2+\displaystyle\frac{1}{24}x^4-\displaystyle\frac{1}{720}x^6+\cdots
\\\\&=
\displaystyle\sum_{n=0}^\infty
\displaystyle\frac{(-1)^n}{(2n)!}
x^{2n}
~~~~(-\infty<x<\infty)
\end{align}
$$
$$
\begin{align}
\displaystyle\frac{1}{1-x}
&=
1+x^2+x^3+x^4+\cdots
\\\\&=
\displaystyle\sum_{n=0}^\infty
x^n
~~~~(-1<x<1)
\end{align}
$$
まとめ
収束半径$R$の公式は以下の式です。
$$
R
=
\displaystyle\lim_{n \to \infty}
\left|
\displaystyle\frac{c_n}{c_{n+1}}
\right|
$$
この$R$の値を用いて以下のようにテイラー展開できる範囲が決まります。
- $|x|<R$ならテイラー展開可能
- $|x|>R$ならテイラー展開不可能
- $|x|=R$のテイラー展開は個別調査が必要





コメント欄