こんにちはコーヤです。
このページでは、式変形と公式を組み合わせて関数の極限を求める正攻法を勉強します。ロピタルの定理やテイラー展開で極限を求めるよりも楽に計算できます。
数列の極限と関数の極限の違い
関数の極限は数列の極限の延長線上です。計算方法も似たような感じになります。
1つだけ大きな違いがあり、数列の極限は$n\to\infty$のパターンしかありませんでしたが、関数の極限は$x\to -\infty$や$x\to \pi$などいろんなパターンがあることです。
計算方法が思いつかない場合は、新たに変数を作って$x\to\infty$や$x\to0$のような見慣れた極限に変形することが重要です。
数列の極限が不安な方は復習がてらご覧ください。
関数の極限の計算方針3種類
関数の極限の計算は主に3種類の方針があります。
- 式変形と公式を組み合わせる正攻法
- ロピタルの定理を使う
- テイラー展開を使う
このページでは1の正攻法にフォーカスして勉強します。
ロピタルの定理は使用できるかどうかの判断が面倒、テイラー展開は計算量が多い、というデメリットがありますが、正攻法にはデメリットがありません。
ロピタルの定理とテイラー展開(ランダウの記号を用いたテイラー展開)で極限を求める方法はそれぞれ以下のページをご覧ください。
正攻法の式変形パターン7つ
正攻法の頻出パターンを7つ列挙します。全て解けるようになっておきましょう。
- 約分
- 有理化
- 三角関数
- 指数関数・対数関数
- 逆三角関数
- 双曲線関数
- 片側極限
パターン1. 約分
最初に疑うべきは約分できるかどうかです。
$$
\begin{array}{cl}
(1) & \displaystyle\lim_{x \to 1}
\displaystyle\frac{x^2-1}{x-1}
\\\\
(2) & \displaystyle\lim_{x \to \pi}
\displaystyle\frac{1+\cos x}{\sin ^2 x}
\end{array}
$$
(1)は分母分子を$x-1$で約分することで計算できるようになります。
$$
\begin{align}
\displaystyle\lim_{x \to 1}
\displaystyle\frac{x^2-1}{x-1}
&=
\displaystyle\lim_{x \to 1}
\displaystyle\frac{(x-1)(x+1)}{x-1}
\\\\&=
\displaystyle\lim_{x \to 1}
(x+1)
\\\\&=
2
\end{align}
$$
(2)は$\sin ^2 x$を$\cos x$で表せば約分できるようになります。
$$
\begin{align}
\displaystyle\lim_{x \to \pi}
\displaystyle\frac{1+\cos x}{\sin ^2 x}
&=
\displaystyle\lim_{x \to \pi}
\displaystyle\frac{1+\cos x}{1-\cos ^2 x}
\\\\&=
\displaystyle\lim_{x \to \pi}
\displaystyle\frac{1+\cos x}{(1+\cos x)(1-\cos x)}
\\\\&=
\displaystyle\lim_{x \to \pi}
\displaystyle\frac{1}{1-\cos x}
\\\\&=
\displaystyle\frac{1}{2}
\end{align}
$$
パターン2. 有理化
ルートがあるときは有理化するパターンがほとんどです。
$x\to -\infty$のときは$x=-\sqrt{x^2}$となることに注意が必要です。最初に$x=-t$として$t\to\infty$の極限に変換すると楽です。
$$
\begin{array}{cl}
(1) & \displaystyle\lim_{x \to 0}
\displaystyle\frac{\sqrt{1+x}-\sqrt{1-x}}{x}
\\\\
(2) & \displaystyle\lim_{x \to -\infty}
\displaystyle\frac{x+1}{\sqrt{x^2+1}-x}
\end{array}
$$
(1)は有理化すればおしまいです。
$$
\begin{align}
\displaystyle\lim_{x \to 0}
\displaystyle\frac{\sqrt{1+x}-\sqrt{1-x}}{x}
&=
\displaystyle\lim_{x \to 0}
\displaystyle\frac{2}{\sqrt{1+x}+\sqrt{1-x}}
\\\\&=
1
\end{align}
$$
(2)は符号ミス頻発問題です。最初に$x=-t$と変換して$t\to\infty$の極限に変換します。
$$
\displaystyle\lim_{x \to -\infty}
\displaystyle\frac{x+1}{\sqrt{x^2+1}-x}
=
\displaystyle\lim_{t \to \infty}
\displaystyle\frac{-t+1}{\sqrt{t^2+1}+t}
$$
分母分子を$t$で割って
$$
\begin{align}
\displaystyle\lim_{t \to \infty}
\displaystyle\frac{-t+1}{\sqrt{t^2+1}+t}
&=
\displaystyle\lim_{t \to \infty}
\displaystyle\frac{-1+\displaystyle\frac{1}{t}}{\sqrt{1+\displaystyle\frac{1}{t^2}}+1}
\\\\&=
-\displaystyle\frac{1}{2}
\end{align}
$$
となります。
$x=-t$と変換しない場合は以下のようになります。$x=-\sqrt{x^2}$になることに注意です。
$$
\begin{align}
\displaystyle\lim_{x \to -\infty}
\displaystyle\frac{x+1}{\sqrt{x^2+1}-x}
&=
\displaystyle\lim_{x \to -\infty}
\displaystyle\frac{1+\displaystyle\frac{1}{x}}{\displaystyle\frac{\sqrt{x^2+1}}{x}-1}
\\\\&=
\displaystyle\lim_{x \to -\infty}
\displaystyle\frac{1+\displaystyle\frac{1}{x}}{\displaystyle\frac{\sqrt{x^2+1}}{-\sqrt{x^2}}-1}
\\\\&=
\displaystyle\lim_{x \to -\infty}
\displaystyle\frac{1+\displaystyle\frac{1}{x}}{-\sqrt{1+\displaystyle\frac{1}{x^2}}-1}
\\\\&=
-\displaystyle\frac{1}{2}
\end{align}
$$
パターン3. 三角関数
三角関数の極限の公式は以下3つです。
$$
\begin{array}{l}
\displaystyle\lim_{x \to 0}
\displaystyle\frac{\sin x}{x}
=
1
\\\\
\displaystyle\lim_{x \to 0}
\displaystyle\frac{\tan x}{x}
=
1
\\\\
\displaystyle\lim_{x \to 0}
\displaystyle\frac{1-\cos x}{x^2}
=
\displaystyle\frac{1}{2}
\end{array}
$$
この公式が使えるように式変形をしていけば極限が求まります。
$$
\begin{array}{cl}
(1) & \displaystyle\lim_{x \to 0}
\displaystyle\frac{1}{\sin x}
-\displaystyle\frac{1}{\tan x}
\\\\
(2) & \displaystyle\lim_{x \to \frac{1}{4}\pi}
\displaystyle\frac{\sin x -\cos x}{4x-\pi}
\end{array}
$$
(1)は式変形して公式を使える形にします。
$$
\begin{align}
\displaystyle\lim_{x \to 0}
\displaystyle\frac{1}{\sin x}
-\displaystyle\frac{1}{\tan x}
&=
\displaystyle\lim_{x \to 0}
\displaystyle\frac{1}{\sin x}
-\displaystyle\frac{\cos x}{\sin x}
\\\\&=
\displaystyle\lim_{x \to 0}
\displaystyle\frac{1-\cos x}{\sin x}
\\\\&=
\displaystyle\lim_{x \to 0}
\displaystyle\frac{1-\cos x}{x^2}
\cdot
\displaystyle\frac{x}{\sin x}
\cdot
x
\\\\&=
\displaystyle\frac{1}{2}
\cdot
1
\cdot
0
\\\\&=
0
\end{align}
$$
(2)は分子の三角関数を合成します。
$$
\displaystyle\lim_{x \to \frac{1}{4}\pi}
\displaystyle\frac{\sin x -\cos x}{4x-\pi}
=
\displaystyle\lim_{x \to \frac{1}{4}\pi}
\displaystyle\frac{\sqrt{2}\sin \left( x-\displaystyle\frac{1}{4}\pi \right)}{4\left( x-\displaystyle\frac{1}{4}\pi \right)}
$$
ここで$t=x-\frac{1}{4}\pi$として
$$
\begin{align}
\displaystyle\lim_{x \to \frac{1}{4}\pi}
\displaystyle\frac{\sqrt{2}\sin \left( x-\displaystyle\frac{1}{4}\pi \right)}{4\left( x-\displaystyle\frac{1}{4}\pi \right)}
&=
\displaystyle\lim_{t \to 0}
\displaystyle\frac{\sqrt{2}\sin t}{4t}
\\\\&=
\displaystyle\frac{\sqrt{2}}{4}
\end{align}
$$
パターン4. 指数関数・対数関数
指数関数と対数関数の極限の公式は以下3つです。
$$
\begin{array}{l}
\displaystyle\lim_{x \to 0}
(1+x)^{\frac{1}{x}}
=
e
\\\\
\displaystyle\lim_{x \to 0}
\displaystyle\frac{\log (1+x)}{x}
=
1
\\\\
\displaystyle\lim_{x \to 0}
\displaystyle\frac{e^x-1}{x}
=
1
\end{array}
$$
この公式が使えるように式変形をしていけば極限が求まります。
$$
\begin{array}{cl}
(1) & \displaystyle\lim_{x \to \infty}
x
\left\{
\log(x+1)-\log x
\right\}
\\\\
(2) & \displaystyle\lim_{x \to \infty}
\left(
\displaystyle\frac{x-1}{x+1}
\right)
^x
\end{array}
$$
(1)は式変形して公式を使える形にします。
$$
\begin{align}
\displaystyle\lim_{x \to \infty}
x
\left\{
\log(x+1)-\log x
\right\}
&=
\displaystyle\lim_{x \to \infty}
x\log \displaystyle\frac{x+1}{x}
\\\\&=
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{\log\left(1+\displaystyle\frac{1}{x}\right)}{\displaystyle\frac{1}{x}}
\\\\&=
1
\end{align}
$$
(2)は分子を分母で割って変形します。
$$
\begin{align}
\displaystyle\lim_{x \to \infty}
\left(
\displaystyle\frac{x-1}{x+1}
\right)
^x
&=
\displaystyle\lim_{x \to \infty}
\left(
1-\displaystyle\frac{2}{x+1}
\right)
^x
\\\\&=
\displaystyle\lim_{x \to \infty}
\left(
1+\displaystyle\frac{-2}{x+1}
\right)
^{\frac{x+1}{-2}\cdot\frac{-2x}{x+1}}
\\\\&=
\displaystyle\lim_{x \to \infty}
e
^{\frac{-2x}{x+1}}
\\\\&=
e^{-2}
\end{align}
$$
パターン5. 逆三角関数
逆三角関数が出てきたら$\arcsin x=t$のようにおくだけで三角関数のパターンに帰着できます。
$$
\begin{array}{cl}
(1) & \displaystyle\lim_{x \to 0}
\arctan \displaystyle\frac{1}{x}
\\\\
(2) & \displaystyle\lim_{x \to 0}
\displaystyle\frac{\arcsin x}{\tan x}
\end{array}
$$
(1)は$\arctan x$のグラフの概形が思い浮かべば瞬殺です。
$\arctan \displaystyle\frac{1}{x}=t$とすると$t\to \displaystyle\frac{1}{2}\pi$になります。
$$
\begin{align}
\displaystyle\lim_{x \to 0}
\arctan \displaystyle\frac{1}{x}
&=
\displaystyle\lim_{t \to \frac{1}{2}\pi}
t
\\\\&=
\displaystyle\frac{1}{2}\pi
\end{align}
$$
(2)も同様に$\arcsin x=t$とおいて$t\to 0$の極限に変形します。
$\arcsin x=t$より$\sin t=x$なので$\displaystyle\frac{x}{\sin t}=1$となることを利用します。
$$
\begin{align}
\displaystyle\lim_{x \to 0}
\displaystyle\frac{\arcsin x}{\tan x}
&=
\displaystyle\lim_{t \to 0}
\displaystyle\frac{t}{\tan x}
\\\\&=
\displaystyle\lim_{t \to 0}
\displaystyle\frac{t}{\tan x}
\cdot
\displaystyle\frac{x}{\sin t}
\\\\&=
\displaystyle\lim_{t \to 0}
\displaystyle\frac{t}{\sin t}
\cdot
\displaystyle\frac{x}{\tan x}
\\\\&=
1\cdot 1
\\\\&=
1
\end{align}
$$
パターン6. 双曲線関数
双曲線関数は指数関数に変形するだけです。
$$
\begin{array}{l}
\sinh x
=
\displaystyle\frac{e^x-e^{-x}}{2}
\\\\
\cosh x
=
\displaystyle\frac{e^x+e^{-x}}{2}
\\\\
\tanh x
=
\displaystyle\frac{e^x-e^{-x}}{e^x+e^{-x}}
\end{array}
$$
この変形で指数関数のパターンに帰着させます。
$$
\begin{array}{cl}
(1) & \displaystyle\lim_{x \to 0}
\displaystyle\frac{\sinh x}{x}
\\\\
(2) & \displaystyle\lim_{x \to 0}
\displaystyle\frac{\cosh x-1}{x^2}
\end{array}
$$
(1)は変形してから分母分子に$e^x$をかけます。
$$
\begin{align}
\displaystyle\lim_{x \to 0}
\displaystyle\frac{\sinh x}{x}
&=
\displaystyle\lim_{x \to 0}
\displaystyle\frac{e^x-e^{-x}}{2x}
\\\\&=
\displaystyle\lim_{x \to 0}
\displaystyle\frac{e^{2x}-1}{2xe^x}
\\\\&=
\displaystyle\lim_{x \to 0}
\displaystyle\frac{e^{2x}-1}{2x}
\cdot
\displaystyle\frac{1}{e^x}
\\\\&=
1\cdot 1
\\\\&=
1
\end{align}
$$
(2)は因数分解が必要です。
$$
\begin{align}
\displaystyle\lim_{x \to 0}
\displaystyle\frac{\cosh x-1}{x^2}
&=
\displaystyle\lim_{x \to 0}
\displaystyle\frac{e^x+e^{-x}-2}{2x^2}
\\\\&=
\displaystyle\lim_{x \to 0}
\displaystyle\frac{e^{2x}-2e^x+1}{2x^2e^x}
\\\\&=
\displaystyle\lim_{x \to 0}
\displaystyle\frac{(e^x-1)^2}{2x^2e^x}
\\\\&=
\displaystyle\lim_{x \to 0}
\left(
\displaystyle\frac{e^x-1}{x}
\right)
^2
\cdot
\displaystyle\frac{1}{2e^x}
\\\\&=
1^2 \cdot \displaystyle\frac{1}{2}
\\\\&=
\displaystyle\frac{1}{2}
\end{align}
$$
パターン7. 片側極限
極限の前後で関数の振る舞いが異なるときは右側極限と左側極限に分けて考えないといけません。
右側極限と左側極限の値が一致すればその値を極限として扱います。一致しなければ極限なしとなります。
$$
\begin{array}{cl}
(1) & \displaystyle\lim_{x \to 0}
\displaystyle\frac{1}{x}
\\\\
(2) & \displaystyle\lim_{x \to 0}
\displaystyle\frac{1}{x^2}
\end{array}
$$
(1)と(2)のグラフをそれぞれ示します。
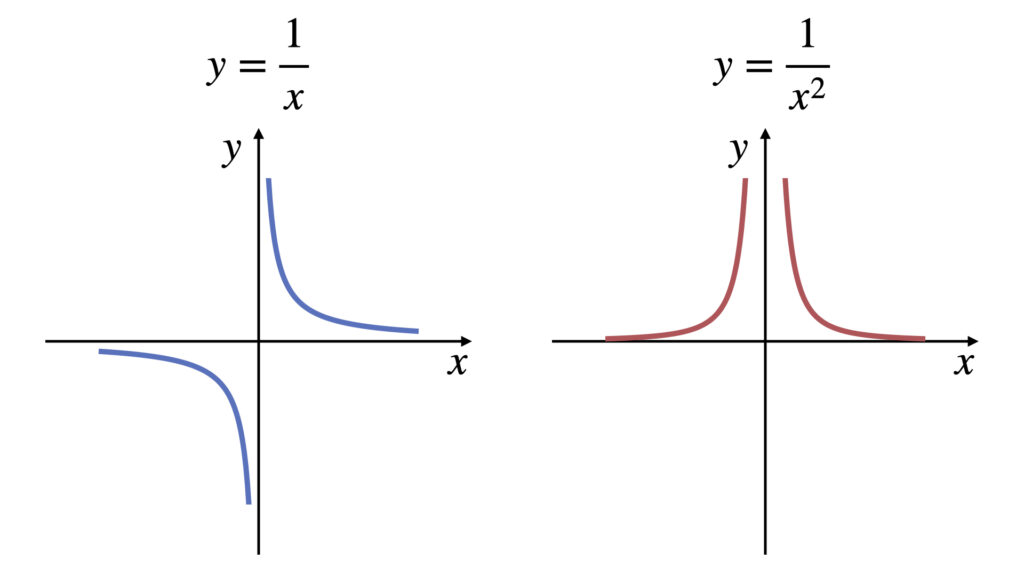
グラフより(1)は
$$
\begin{align}
\displaystyle\lim_{x \to +0}
\displaystyle\frac{1}{x}
&=
\infty
\\\\
\displaystyle\lim_{x \to -0}
\displaystyle\frac{1}{x}
&=
-\infty
\end{align}
$$
右側極限と左側極限が一致しないので極限なしです。
グラフより(2)は
$$
\begin{align}
\displaystyle\lim_{x \to +0}
\displaystyle\frac{1}{x^2}
&=
\infty
\\\\
\displaystyle\lim_{x \to -0}
\displaystyle\frac{1}{x^2}
&=
\infty
\end{align}
$$
右側極限と左側極限が一致するので
$$
\displaystyle\lim_{x \to 0}
\displaystyle\frac{1}{x^2}
=
\infty
$$
です。
両方とも$x=0$のときは定義されない関数ですが、$x\to 0$の値と$x=0$の値は関係ありません。
関数の極限の例題
それでは例題6つで関数の極限を求めてみましょう。
例題1
$$
\displaystyle\lim_{x \to 0}
x^2 \log(1-\cos x)
$$
$\cos x$の公式が使えるように式変形します。$\log x$の公式は使いません。
$$
\begin{align}
\displaystyle\lim_{x \to 0}
x^2 \log(1-\cos x)
&=
\displaystyle\lim_{x \to 0}
\displaystyle\frac{x^2}{1-\cos x}
\cdot
(1-\cos x)
\cdot
\log(1-\cos x)
\\\\&=
\displaystyle\lim_{x \to 0}
2
\cdot
(1-\cos x)
\cdot
\log(1-\cos x)
\end{align}
$$
ここで$1-\cos x=t$とおいて$t \to 0$の極限に変形します。
$-1 \leq \cos x \leq 1$より$t \to 0$は$t \to +0$になります。
$$
\begin{align}
\displaystyle\lim_{x \to 0}
2
\cdot
(1-\cos x)
\cdot
\log(1-\cos x)
&=
\displaystyle\lim_{t \to +0}
2
\cdot
t
\cdot
\log t
\\\\&=
0
\end{align}
$$
となります。
$t\cdot\log t$の部分は、$\log t \to -\infty$と発散する速度より$t\to 0$に収束する速度のほうが速いです。
したがって$t\cdot\log t \to 0$になります。
例題2
$$
\displaystyle\lim_{x \to 0}
\displaystyle\frac{x}{\pi ^x-1}
$$
この問題はハッタリみたいな問題です。$\pi=e^{\log \pi}$と変形すればすぐに公式が使えます。
$$
\begin{align}
\displaystyle\lim_{x \to 0}
\displaystyle\frac{x}{\pi ^x-1}
&=
\displaystyle\lim_{x \to 0}
\displaystyle\frac{x}{\left( e^{\log \pi} \right) ^x-1}
\\\\&=
\displaystyle\lim_{x \to 0}
\displaystyle\frac{\left( \log \pi \right)x}{e^{\left( \log \pi \right)x}-1}
\cdot
\displaystyle\frac{1}{\log \pi}
\\\\&=
1
\cdot
\displaystyle\frac{1}{\log \pi}
\\\\&=
\displaystyle\frac{1}{\log \pi}
\end{align}
$$
例題3
$$
\displaystyle\lim_{x \to \infty}
\left(
\cos \displaystyle\frac{1}{x}
\right)
^{x^2}
$$
見た目的に三角関数の公式を使いたくなりますが、指数関数の公式を使えるように変形するのがポイントです。
$1+t=\cos \displaystyle\frac{1}{x}$とおいて$t\to 0$の極限に変形します。
$-1 \leq \cos \displaystyle\frac{1}{x} \leq 1$より$t \to 0$は$t \to -0$になります。
$$
\begin{align}
\displaystyle\lim_{x \to \infty}
\left(
\cos \displaystyle\frac{1}{x}
\right)
^{x^2}
&=
\displaystyle\lim_{t \to -0}
(1+t)^{x^2}
\\\\&=
\displaystyle\lim_{t \to -0}
\left\{
(1+t)^{\frac{1}{t}}
\right\}
^{tx^2}
\\\\&=
\displaystyle\lim_{t \to -0}
e^{tx^2}
\end{align}
$$
ここで$tx^2$の部分を考えます。
$$
\begin{align}
\displaystyle\lim_{t \to -0}
tx^2
&=
\displaystyle\lim_{x \to \infty}
\left(
\cos \displaystyle\frac{1}{x}-1
\right)
x^2
\\\\&=
\displaystyle\lim_{x \to \infty}
-\displaystyle\frac{1-\cos\displaystyle\frac{1}{x}}{\left(\displaystyle\frac{1}{x}\right)^2}
\\\\&=
-\displaystyle\frac{1}{2}
\end{align}
$$
これを代入して
$$
\begin{align}
\displaystyle\lim_{t \to -0}
e^{tx^2}
&=
e^{-\frac{1}{2}}
\\\\&=
\displaystyle\frac{1}{\sqrt{e}}
\end{align}
$$
となります。
例題4
$$
\displaystyle\lim_{x \to 0}
\displaystyle\frac{\tanh(\arcsin x)}{x}
$$
逆三角関数を見かけたら文字でおくところから始めます。それから双曲線関数を処理しましょう。
$\arcsin x=t$として$t\to 0$の極限に変形します。
$$
\begin{align}
\displaystyle\lim_{x \to 0}
\displaystyle\frac{\tanh(\arcsin x)}{x}
&=
\displaystyle\lim_{t \to 0}
\displaystyle\frac{\tanh t}{\sin t}
\\\\&=
\displaystyle\lim_{t \to 0}
\displaystyle\frac{e^t-e^{-t}}{e^t+e^{-t}}
\cdot
\displaystyle\frac{1}{\sin t}
\\\\&=
\displaystyle\lim_{t \to 0}
\displaystyle\frac{e^{2t}-1}{e^{2t}+1}
\cdot
\displaystyle\frac{1}{\sin t}
\\\\&=
\displaystyle\lim_{t \to 0}
\displaystyle\frac{e^{2t}-1}{2t}
\cdot
\displaystyle\frac{2}{e^{2t}+1}
\cdot
\displaystyle\frac{t}{\sin t}
\\\\&=
1\cdot 1\cdot 1
\\\\&=
1
\end{align}
$$
例題5
$$
\displaystyle\lim_{x \to \infty}
x^{\frac{1}{x}}
$$
一見難しそうですが、極限の値を$p$として式変形します。
$$
p
=
\displaystyle\lim_{x \to \infty}
x^{\frac{1}{x}}
$$
両辺$\log$を取って
$$
\begin{align}
\log p
&=
\displaystyle\lim_{x \to \infty}
\log
x^{\frac{1}{x}}
\\\\&=
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{\log x}{x}
\\\\&=
0
\end{align}
$$
対数関数よりも冪関数の方が発散の速度が速いので0になります。
$\log$を取ると以下の対応関係なので
$$
\begin{align}
\log p &= 0
\\\\
p &= 1
\end{align}
$$
以上の結果より
$$
\displaystyle\lim_{x \to \infty}
x^{\frac{1}{x}}
=
1
$$
です。
例題6
$$
\displaystyle\lim_{x \to 0}
\left(
\displaystyle\frac{\sin x}{x}
\right)
^{\frac{1}{x^2}}
$$
残念ながら正攻法では解けません。
こういう場合はロピタルの定理かテイラー展開の出番です。
ロピタルの定理で解くやり方はロピタルのページで解説しています。
テイラー展開で解くやり方はランダウの記号のページで解説しています。
まとめ
正攻法の頻出パターンを7つ列挙します。
- 約分
- 有理化
- 三角関数
- 指数関数・対数関数
- 逆三角関数
- 双曲線関数
- 片側極限
公式が使えるように式変形を工夫して、知っているパターンに帰着させたら計算できます。






コメント欄