こんにちはコーヤです。
このページでは正規直交基底の性質とグラムシュミットの正規直交化法について勉強します。どんな基底でも正規直交基底に変換できるようになります。
正規直交基底の条件1つ
内積空間である3次元列ベクトル空間$R^3$として$\langle \boldsymbol{e}_1 , \boldsymbol{e}_2 , \boldsymbol{e}_3 \rangle$と$\langle \boldsymbol{f}_1 , \boldsymbol{f}_2 , \boldsymbol{f}_3 \rangle$の2組を考えてみます。
正規直交基底は線形空間の基底の応用編です。基底が不安な方はまず基底のページをご覧ください。
$$
\left.
\begin{array}{ccc}
\boldsymbol{e}_1
=
\begin{pmatrix}
1 \\
0 \\
0
\end{pmatrix}
&
\boldsymbol{e}_2
=
\begin{pmatrix}
0 \\
1 \\
0
\end{pmatrix}
&
\boldsymbol{e}_3
=
\begin{pmatrix}
0 \\
0 \\
1
\end{pmatrix}
\end{array}
\right.
$$
$$
\left.
\begin{array}{ccc}
\boldsymbol{f}_1
=
\begin{pmatrix}
1 \\
1 \\
0
\end{pmatrix}
&
\boldsymbol{f}_2
=
\begin{pmatrix}
0 \\
2 \\
1
\end{pmatrix}
&
\boldsymbol{f}_3
=
\begin{pmatrix}
2 \\
2 \\
3
\end{pmatrix}
\end{array}
\right.
$$
線形空間の基底は2つの条件を満たせばどんな定め方をしてもOKでした。
- 線形独立であること
- 線形結合で任意の元を表せること
内積空間の基底もこの2つを満たせばどんな定め方をしてもOKですが、さらに1つ条件を追加してみます。
内積空間の基底$\langle \boldsymbol{u}_1,\boldsymbol{u}_2\cdots \boldsymbol{u}_n \rangle$が
$$
\begin{array}{cc}
\boldsymbol{u}_i \cdot \boldsymbol{u}_j = \delta_{ij}
&
(i,j=1,2,\cdots n)
\end{array}
$$
を満たす時、基底$\langle \boldsymbol{u}_1,\boldsymbol{u}_2\cdots \boldsymbol{u}_n \rangle$を正規直交基底と言います。
$\delta_{ij}$はクロネッカーのデルタと呼ばれる数です。以下のように0か1かどちらかになります。
$$
\delta_{ij}
=
\left\{
\begin{array}{ll}
1 & (i=j) \\
0 & (i \neq j)
\end{array}
\right.
$$
正規直交基底の意味
正規直交基底の条件がどういう意味か考えてみます。
$\delta_{ij}=1$のパターンは
$$
\boldsymbol{u}_i \cdot \boldsymbol{u}_i
=
\|\boldsymbol{u}_i\|^2
=
1
$$
となります。ノルムの性質より$\| \boldsymbol{u}_i \| \geqq 0$なので
$$
\|\boldsymbol{u}_i\|=1
$$
です。つまり、基底のノルムが1になるという条件を表しています。そして、ノルムを1にすることを「正規化する」といいます。
次に$\delta_{ij}=0$のパターンについて、直交の性質より
$$
\begin{array}{ccc}
\boldsymbol{u}_i \cdot \boldsymbol{u}_j=0
&
\Leftrightarrow
&
\boldsymbol{u}_i \perp \boldsymbol{u}_j
\end{array}
$$
となります。つまり、異なる基底同士は直交しているという条件を表しています。
まとめると正規直交基底は
- 基底が正規化されている
- 異なる基底同士が直交する
この2つの条件を満たす内積空間の基底のことです。
正規直交基底の判定方法
冒頭の$\langle \boldsymbol{e}_1 , \boldsymbol{e}_2 , \boldsymbol{e}_3 \rangle$と$\langle \boldsymbol{f}_1 , \boldsymbol{f}_2 , \boldsymbol{f}_3 \rangle$が正規直交基底かどうか判定してみます。
お察しの通り$\langle \boldsymbol{e}_1 , \boldsymbol{e}_2 , \boldsymbol{e}_3 \rangle$は$R^3$の正規直交基底です。
$$
\begin{align}
\boldsymbol{e}_1 \cdot \boldsymbol{e}_1
=
\boldsymbol{e}_2 \cdot \boldsymbol{e}_2
=
\boldsymbol{e}_3 \cdot \boldsymbol{e}_3
=
1
\\\\
\boldsymbol{e}_1 \cdot \boldsymbol{e}_2
=
\boldsymbol{e}_2 \cdot \boldsymbol{e}_3
=
\boldsymbol{e}_3 \cdot \boldsymbol{e}_1
=
0
\end{align}
$$
計算してみるとたしかに正規直交基底の条件を満たします。
見た目的にもノルムが1ですし、お互い直交してそうな感じがします。
次は$\langle \boldsymbol{f}_1 , \boldsymbol{f}_2 , \boldsymbol{f}_3 \rangle$を調べてみます。
$$
\boldsymbol{f}_1 \cdot \boldsymbol{f}_1
=
2
$$
この時点でアウトです。残念ながら$\langle \boldsymbol{f}_1 , \boldsymbol{f}_2 , \boldsymbol{f}_3 \rangle$は$R^3$の正規直交基底ではありません。
でもこれで終わりではありません。内積空間はどんな意地悪な基底で作られていても、グラム・シュミットの正規直交化法という計算で正規直交基底に変換することができます。
グラム・シュミットの正規直交化法
グラム・シュミットの正規直交化法で意地悪なの基底が作っている内積空間を正規直交基底で表現することができます。
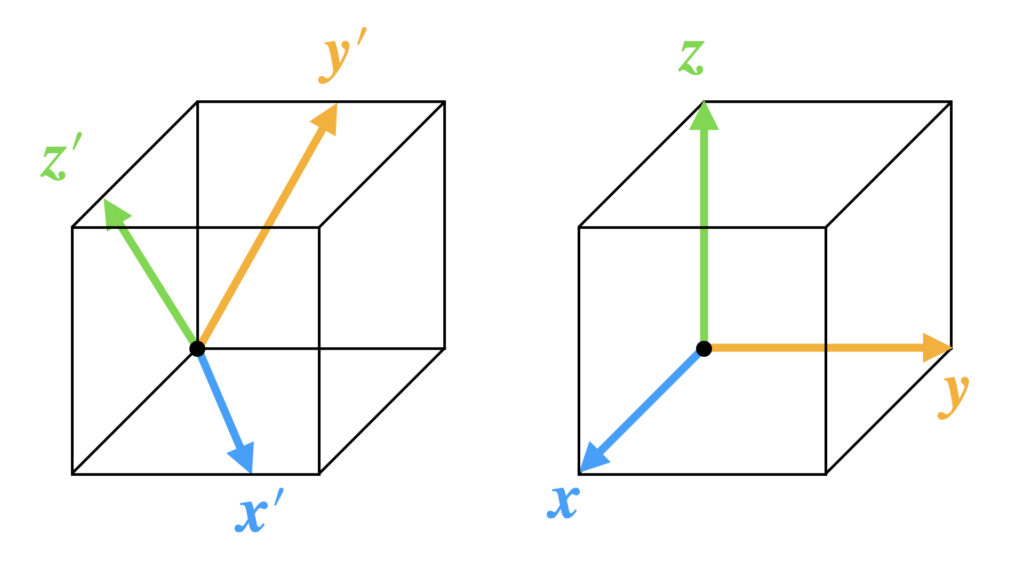
3次元内積空間$R^3$の基底として画像左側の$\langle \boldsymbol{x}’ , \boldsymbol{y}’ , \boldsymbol{z}’ \rangle$と画像右側の$\langle \boldsymbol{x} , \boldsymbol{y} , \boldsymbol{z} \rangle$があります。
どちらも基底としてはOKですが右側の$\langle \boldsymbol{x} , \boldsymbol{y} , \boldsymbol{z} \rangle$の方が分かりやすいです。
グラム・シュミットの正規直交化法を使うと$\langle \boldsymbol{x}’ , \boldsymbol{y}’ , \boldsymbol{z}’ \rangle$で与えられた内積空間の空間の形はそのままに、基底を$\langle \boldsymbol{x} , \boldsymbol{y} , \boldsymbol{z} \rangle$に変換できます。
それでは具体的な計算方法を見ていきます。上の例で使った$\langle \boldsymbol{f}_1 , \boldsymbol{f}_2 , \boldsymbol{f}_3 \rangle$を正規直交基底$\langle \boldsymbol{u}_1 , \boldsymbol{u}_2 , \boldsymbol{u}_3 \rangle$に変換します。
計算の流れは
- 他の変換済み基底$\boldsymbol{u}_1,\boldsymbol{u}_2 \cdots \boldsymbol{u}_{i-1}$と直交する$\boldsymbol{g}_i$をつくる
- $\boldsymbol{g}_i$を正規化して$\boldsymbol{u}_i$をつくる
を$\boldsymbol{f}_1 , \boldsymbol{f}_2 , \boldsymbol{f}_3$の順にやっていきます。
$\boldsymbol{f}_1$を変換
まずは1つ目の基底$\boldsymbol{f}_1$を正規直交基底$\boldsymbol{u}_1$に変換します。$\boldsymbol{f}_2 , \boldsymbol{f}_3$は無視します。
まずは他の変換済み基底と直交する$\boldsymbol{g}_1$を作る段階ですが、まだ他の変換済み基底がありません。なので
$$
\boldsymbol{g}_1
=
\boldsymbol{f}_1
$$
とします。
次に$\boldsymbol{g}_1$を正規化したものを$\boldsymbol{u}_1$とします。
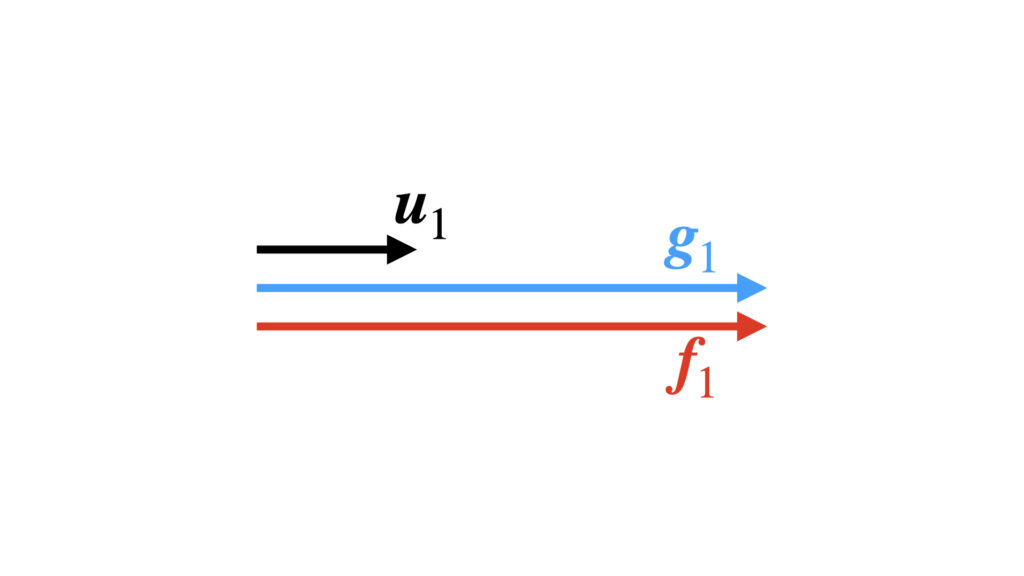
$\boldsymbol{g}_1$と同じ方向の正規化されたベクトル$\boldsymbol{u}_1$は以下のように計算すると求まります。
$$
\boldsymbol{u}_1
=
\displaystyle \frac
{1}
{\|\boldsymbol{g}_1\|}
\boldsymbol{g}_1
$$
数値をいれて計算すると
$$
\begin{align}
\boldsymbol{u}_1
&=
\displaystyle \frac
{1}
{\|\boldsymbol{g}_1\|}
\boldsymbol{g}_1
\\\\&=
\displaystyle \frac{1}{\sqrt{2}}
\begin{pmatrix}
1 \\
1 \\
0
\end{pmatrix}
\end{align}
$$
となります。
$\boldsymbol{f}_2$を変換
次は2つ目の基底$\boldsymbol{f}_2$を正規直交基底$\boldsymbol{u}_2$に変換します。$\boldsymbol{f}_3$は無視します。
まずは他の変換済み基底$\boldsymbol{u}_1$と直交する$\boldsymbol{g}_2$を作る段階です。画像のように$\boldsymbol{g}_2$を作ります。
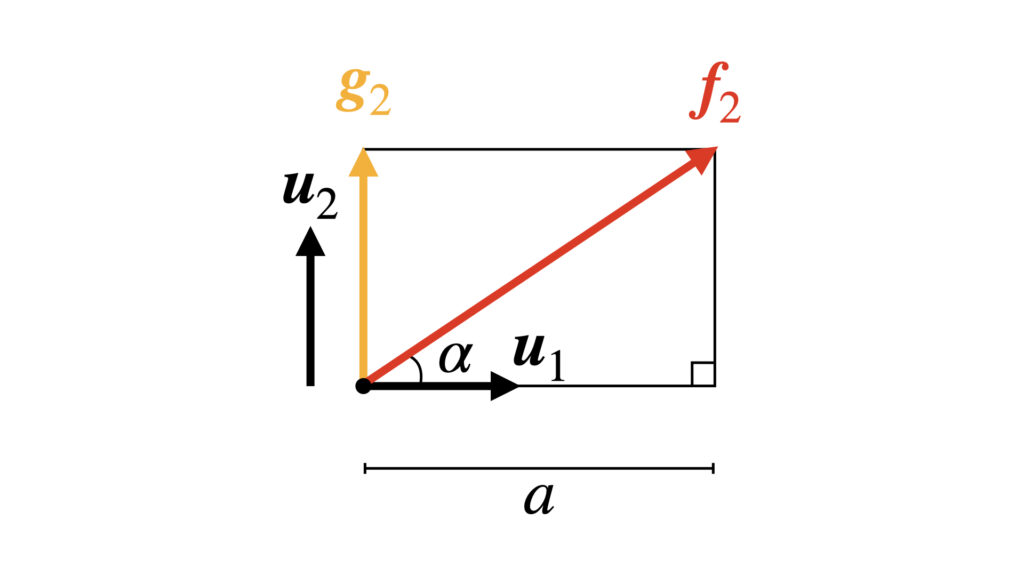
画像より$\boldsymbol{g}_2$は
$$
\boldsymbol{g}_2
=
\boldsymbol{f}_2
-a
\boldsymbol{u}_1
$$
となります。
ここで画像の長さ$a$は
$$
\begin{align}
a
&=
\|\boldsymbol{f}_2\| \cos \alpha
\\\\&=
\|\boldsymbol{u}_1\|\|\boldsymbol{f}_2\| \cos \alpha
\\\\&=
\boldsymbol{u}_1 \cdot \boldsymbol{f}_2
\end{align}
$$
です。2行目で$\|\boldsymbol{u}_1\|$がいきなり出現していますが、$\|\boldsymbol{u}_1\|=1$なので勝手にかけ算してもOKという発想です。
数値をいれて計算すると
$$
\begin{align}
a
&=
\boldsymbol{u}_1 \cdot \boldsymbol{f}_2
\\\\&=
\displaystyle \frac{1}{\sqrt{2}}
\begin{pmatrix}
1 \\
1 \\
0
\end{pmatrix}
\cdot
\begin{pmatrix}
0 \\
2 \\
1
\end{pmatrix}
\\\\&=
\sqrt{2}
\end{align}
$$
$$
\begin{align}
\boldsymbol{g}_2
&=
\boldsymbol{f}_2
-a
\boldsymbol{u}_1
\\\\&=
\begin{pmatrix}
0 \\
2 \\
1
\end{pmatrix}
-\displaystyle \frac{\sqrt{2}}{\sqrt{2}}
\begin{pmatrix}
1 \\
1 \\
0
\end{pmatrix}
\\\\&=
\begin{pmatrix}
-1 \\
1 \\
1
\end{pmatrix}
\end{align}
$$
です。
$\boldsymbol{g}_2$と同じ方向の正規化されたベクトル$\boldsymbol{u}_2$は
$$
\begin{align}
\boldsymbol{u}_2
&=
\displaystyle \frac
{1}
{\|\boldsymbol{g}_2\|}
\boldsymbol{g}_2
\\\\&=
\displaystyle \frac{1}{\sqrt{3}}
\begin{pmatrix}
-1 \\
1 \\
1
\end{pmatrix}
\end{align}
$$
と求まります。
$\boldsymbol{f}_3$を変換
最後3つ目の基底$\boldsymbol{f}_3$を正規直交基底$\boldsymbol{u}_3$に変換します。
まずは他の変換済み基底$\boldsymbol{u}_1,\boldsymbol{u}_2$と直交する$\boldsymbol{g}_3$を作る段階です。画像のように$\boldsymbol{g}_3$を作ります。
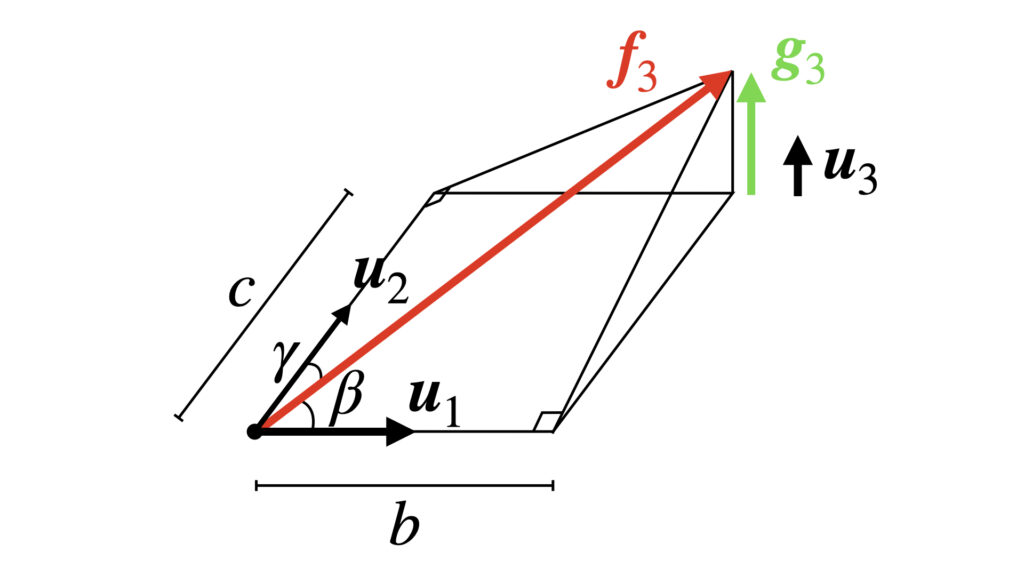
画像より$\boldsymbol{g}_3$は
$$
\boldsymbol{g}_3
=
\boldsymbol{f}_3
-b
\boldsymbol{u}_1
-c
\boldsymbol{u}_2
$$
となります。
ここで画像の長さ$b,c$は$a$を求めたときと同様に
$$
\begin{align}
b
&=
\boldsymbol{u}_1 \cdot \boldsymbol{f}_3
\\\\
c
&=
\boldsymbol{u}_2 \cdot \boldsymbol{f}_3
\end{align}
$$
です。
数値をいれて計算すると
$$
\begin{align}
b
&=
\boldsymbol{u}_1 \cdot \boldsymbol{f}_3
\\\\&=
\displaystyle \frac{1}{\sqrt{2}}
\begin{pmatrix}
1 \\
1 \\
0
\end{pmatrix}
\cdot
\begin{pmatrix}
2 \\
2 \\
3
\end{pmatrix}
\\\\&=
2\sqrt{2}
\end{align}
$$
$$
\begin{align}
c
&=
\boldsymbol{u}_2 \cdot \boldsymbol{f}_3
\\\\&=
\displaystyle \frac{1}{\sqrt{3}}
\begin{pmatrix}
-1 \\
1 \\
1
\end{pmatrix}
\cdot
\begin{pmatrix}
2 \\
2 \\
3
\end{pmatrix}
\\\\&=
\sqrt{3}
\end{align}
$$
$$
\begin{align}
\boldsymbol{g}_3
&=
\boldsymbol{f}_3
-b
\boldsymbol{u}_1
-c
\boldsymbol{u}_2
\\\\&=
\begin{pmatrix}
2 \\
2 \\
3
\end{pmatrix}
-\displaystyle \frac{2\sqrt{2}}{\sqrt{2}}
\begin{pmatrix}
1 \\
1 \\
0
\end{pmatrix}
-\displaystyle \frac{\sqrt{3}}{\sqrt{3}}
\begin{pmatrix}
-1 \\
1 \\
1
\end{pmatrix}
\\\\&=
\begin{pmatrix}
1 \\
-1 \\
2
\end{pmatrix}
\end{align}
$$
です。
$\boldsymbol{g}_3$と同じ方向の正規化されたベクトル$\boldsymbol{u}_3$は
$$
\begin{align}
\boldsymbol{u}_3
&=
\displaystyle \frac
{1}
{\|\boldsymbol{g}_3\|}
\boldsymbol{g}_3
\\\\&=
\displaystyle \frac{1}{\sqrt{6}}
\begin{pmatrix}
1 \\
-1 \\
2
\end{pmatrix}
\end{align}
$$
と求まります。
これで$\boldsymbol{u}_1 , \boldsymbol{u}_2 , \boldsymbol{u}_3$が求まりました。
$$
\left.
\begin{array}{ccc}
\boldsymbol{u}_1
=
\displaystyle \frac{1}{\sqrt{2}}
\begin{pmatrix}
1 \\
1 \\
0
\end{pmatrix}
&
\boldsymbol{u}_2
=
\displaystyle \frac{1}{\sqrt{3}}
\begin{pmatrix}
-1 \\
1 \\
1
\end{pmatrix}
&
\boldsymbol{u}_3
=
\displaystyle \frac{1}{\sqrt{6}}
\begin{pmatrix}
1 \\
-1 \\
2
\end{pmatrix}
\end{array}
\right.
$$
実際に正規直交基底の条件を計算してみると
$$
\begin{align}
\boldsymbol{u}_1 \cdot \boldsymbol{u}_1
=
\boldsymbol{u}_2 \cdot \boldsymbol{u}_2
=
\boldsymbol{u}_3 \cdot \boldsymbol{u}_3
=
1
\\\\
\boldsymbol{u}_1 \cdot \boldsymbol{u}_2
=
\boldsymbol{u}_2 \cdot \boldsymbol{u}_3
=
\boldsymbol{u}_3 \cdot \boldsymbol{u}_1
=
0
\end{align}
$$
を満たしています。$\langle \boldsymbol{f}_1 , \boldsymbol{f}_2 , \boldsymbol{f}_3 \rangle$が基底の内積空間$R^3$から正規直交基底$\langle \boldsymbol{u}_1 , \boldsymbol{u}_2 , \boldsymbol{u}_3 \rangle$の$R^3$に変換できました。
まとめ
正規直交基底は以下2つの条件を満たす内積空間の基底のことです。
- 基底が正規化されている
- 異なる基底同士が直交する
内積空間の基底はグラム・シュミットの正規直交化法で正規直交基底に変換できます。





コメント欄