こんにちはコーヤです。
このページでは特定の条件下での極値の候補を求めるラグランジュの未定乗数法を勉強します。
ラグランジュの未定乗数法の概要
2変数関数$f(x,y)$の極値を求める計算はヘッセシアンで行いました。
ラグランジュの未定乗数法は$g(x,y)=0$の条件下で$f(x,y)$の極値の候補を求める計算方法です。
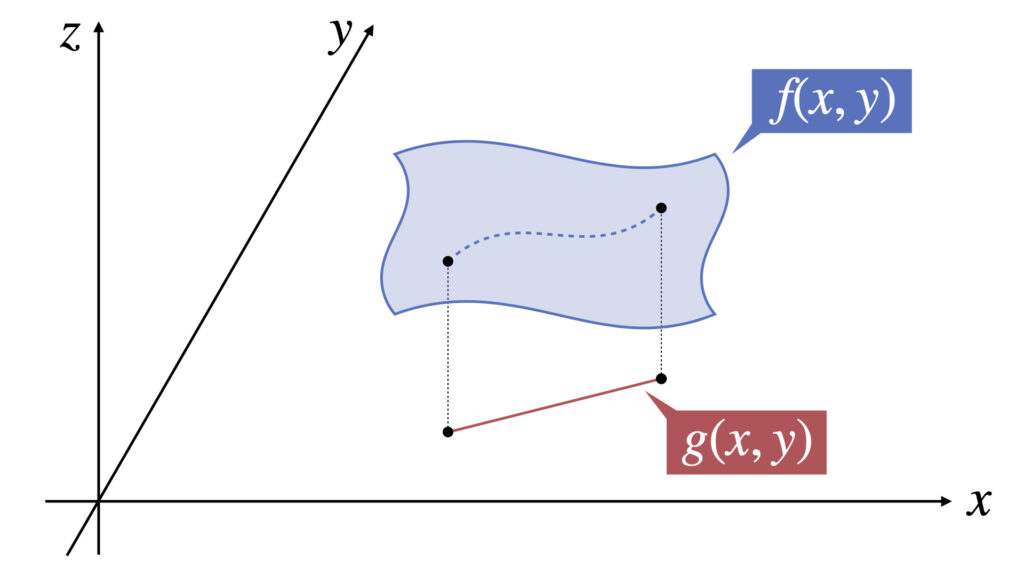
$g(x,y)=0$は図の赤線のように、$xy$平面上の関数です。
これを$z$軸と平行に動かした時に$f(x,y)$と交差する曲線(図の点線)の極値の候補を求めます。
ラグランジュの未定乗数法の公式
ラグランジュ定数$\lambda$を用いてラグランジュ関数$L$を以下のように定義します。
$$
L(x,y,\lambda)
=
f(x,y)-\lambda g(x,y)
$$
このとき
$$
L_x=L_y=L_{\lambda}=0
\tag{1}
$$
$$
g=g_x=g_y=0
\tag{2}
$$
のどちらかを満たす点が極値の候補になります。
ラグランジュの未定乗数法の具体例
それでは公式を使って$y=-x+4$の条件下で$x^2+y^2$の極値の候補を求めてみましょう。
問題文より$f(x,y)$と$g(x,y)=0$に相当する関数は
$$
\begin{align}
f(x,y) &= x^2+y^2
\\\\
g(x,y) &= x+y-4
\end{align}
$$
です。
$f(x,y)$と$g(x,y)$は以下のようなグラフになります。

ラグランジュ関数$L$は
$$
L(x,y,\lambda)
=
x^2+y^2-\lambda(x+y-4)
$$
です。
次に計算に必要な偏導関数を計算します。
$$
\begin{align}
L_x &= 2x-\lambda
\\\\
L_y &= 2y-\lambda
\\\\
L_{\lambda} &= -x-y+4
\\\\
g_x &= 1
\\\\
g_y &= 1
\end{align}
$$
まず式(1)の条件を満たす点を求めます。
$$
L_x=L_y=L_{\lambda}=0
\tag{1}
$$
この条件を3本の式で表して
$$
\begin{align}
0 &= 2x-\lambda
\\\\
0 &= 2y-\lambda
\\\\
0 &= -x-y+4
\end{align}
$$
この連立方程式を解いて
$$
(x,y,\lambda)=(2,2,4)
$$
となります。したがって極値の候補となる点は
$$
(x,y)=(2,2)
$$
です。($\lambda$の値は極値の候補とは無関係です。)
次に式(2)の条件を満たす点を求めます。
$$
g=g_x=g_y=0
\tag{2}
$$
この条件を満たせば良いですが、偏導関数は
$$
g_x = g_y = 1
$$
なので条件を満たせません。したがって式(2)の条件では極値の候補なしです。
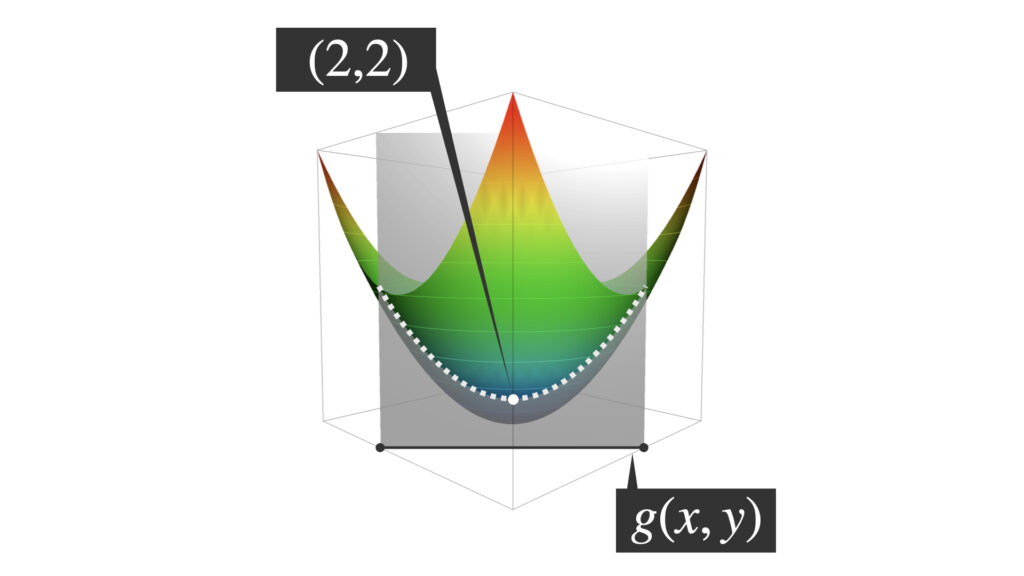
以上の結果より、極値の候補は$(x,y)=(2,2)$だけとなります。
グラフで確認すると、$(x,y)=(2,2)$は$f(x,y)$と$g(x,y)$が交差する線上の極値(の候補)を表しています。
公式の導出
式(1)と式(2)が何を意味しているのかを考えます。
まず式(1)は
$$
\left\{
\begin{array}{l}
L_x=0
\\\\
L_y=0
\end{array}
\right.
\tag{1-1}
$$
$$
0=L_{\lambda}
\tag{1-2}
$$
の2つに分解できます。
式(1-1)について、ラグランジュ関数を$x,y$で偏微分して
$$
\begin{align}
L_x &= f_x-\lambda g_x
\\\\
L_y &= f_y-\lambda g_y
\end{align}
$$
これを式(1-1)に代入して
$$
\left\{
\begin{array}{l}
f_x-\lambda g_x=0
\\\\
f_y-\lambda g_y=0
\end{array}
\right.
$$
移項して
$$
\left\{
\begin{array}{l}
f_x=\lambda g_x
\\\\
f_y=\lambda g_y
\end{array}
\right.
$$
となります。この連立方程式を行列形式で書いて
$$
\begin{pmatrix}
f_x \\ f_y
\end{pmatrix}
=
\lambda
\begin{pmatrix}
g_x \\ g_y
\end{pmatrix}
$$
ここでベクトル$\boldsymbol{f}$と$\boldsymbol{g}$を以下のように定義します。
$$
\begin{align}
\boldsymbol{f}
&=
\begin{pmatrix}
f_x \\ f_y
\end{pmatrix}
\\\\
\boldsymbol{g}
&=
\begin{pmatrix}
g_x \\ g_y
\end{pmatrix}
\end{align}
$$
すると式(1-1)は
$$
\boldsymbol{f}=\lambda \boldsymbol{g}
$$
と書けます。これは$\boldsymbol{f}$と$\boldsymbol{g}$が平行なベクトルであることを表しています。
それでは、ベクトルが平行であることが極値の候補の条件になる理由を考えていきます。
上の具体例で使った
$$
\begin{align}
f(x,y) &= x^2+y^2
\\\\
g(x,y) &= x+y-4
\end{align}
$$
を使いながらベクトルの意味を探ります。
$f(x,y)$の$z=1,4,9$の等位曲線と$g(x,y)=0$を$xy$平面上に書くと以下のようになります。
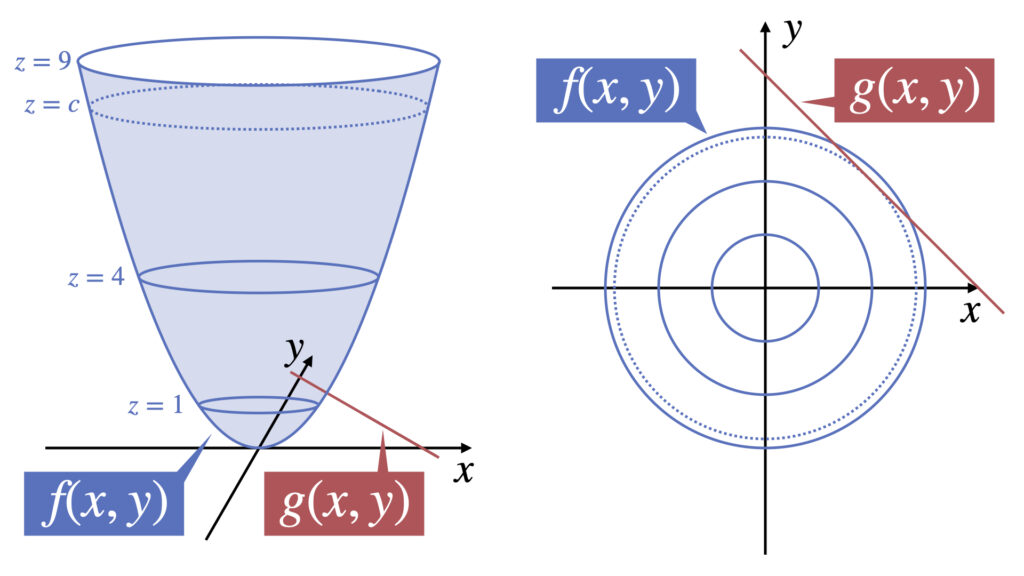
ここで、$z=c$は$xy$平面上で$g(x,y)=0$と接する等位曲線です。
$g(x,y)=0$上の$f(x,y)$の線(白の点線)と、$z=4,c,9$の等位曲線は以下のような位置関係になっています。
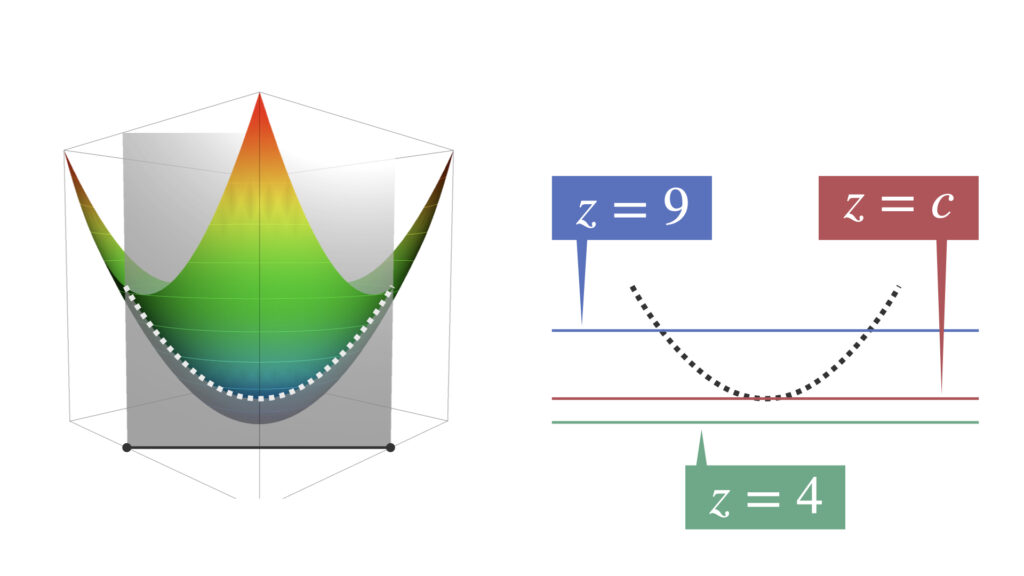
上図の通り、極値の可能性があるのは$z=c$のところだけです。つまり$f(x,y)=c$を満たす点が極値の候補になっているということです。
さて、そのような$c$を求めたいので、$z=c$の等位曲線と$g(x,y)=0$が$xy$平面上で接するという条件から$c$を求めます。
$z=c$の等位曲線と$g(x,y)=0$が接するということは、$z=c$の等位曲線の接線ベクトルと$g(x,y)=0$の接線ベクトルが平行になるはずです。
接線ベクトルが平行になるならそれぞれの勾配$\mathrm{grad}$も平行になるはずです。(接線ベクトルと勾配は直交するため。)

勾配をご存じない方は「法線ベクトル」のことだと思って読んでください。

$f(x,y)$と$g(x,y)$の勾配を計算すると
$$
\begin{align}
\mathrm{grad}~f
&=
\begin{pmatrix}
\displaystyle\frac{\partial f}{\partial x} \\
\displaystyle\frac{\partial f}{\partial y}
\end{pmatrix}
\\\\&=
\begin{pmatrix}
f_x \\ f_y
\end{pmatrix}
\\\\&=
\boldsymbol{f}
\end{align}
$$
$$
\begin{align}
\mathrm{grad}~g
&=
\begin{pmatrix}
\displaystyle\frac{\partial g}{\partial x} \\
\displaystyle\frac{\partial g}{\partial y}
\end{pmatrix}
\\\\&=
\begin{pmatrix}
g_x \\ g_y
\end{pmatrix}
\\\\&=
\boldsymbol{g}
\end{align}
$$
このように、勾配はさきほど使った$\boldsymbol{f}$と$\boldsymbol{g}$と一致します。
つまり、式(1-1)は$g(x,y)=0$と等位曲線が接するという条件を言い換えて、$\boldsymbol{f}$と$\boldsymbol{g}$が平行であると記載しているということです。
式(1-2)について、ラグランジュ関数を$\lambda$で偏微分すると
$$
\begin{align}
0
&=
L_{\lambda}
\\\\&=
\displaystyle\frac{\partial}{\partial \lambda}
\left\{
f(x,y)-\lambda g(x,y)
\right\}
\\\\&=
-g(x,y)
\end{align}
$$
となります。これは問題文で与えられる条件$g(x,y)=0$の書き方を変更しただけです。
次に式(2)について
$$
g=0
\tag{2-1}
$$
$$
g_x=g_y=0
\tag{2-2}
$$
の2つに分解できます。
式(2-1)は問題文で与えられた条件そのままです。
式(2-2)は
$$
\boldsymbol{g}=\mathrm{grad}~g=0
$$
のときを表しています。勾配が0の場合です。
式(1)は$g(x,y)=0$の接線ベクトルと直交する勾配を利用して計算しましたが、そもそも接線が引けないような関数は式(1)では計算できません。
接線が引けない場合を極値の候補に入れるために式(2-2)があります。
複数条件の場合
条件が増えてもラグランジュ関数の作り方は変わりません。
$g(x,y,z)=0$と$h(x,y,z)=0$の条件下で$f(x,y,z)$の極値の候補を求めるときは
$$
L(x,y,z,\lambda)
=
f(x,y,z)-\lambda g(x,y,z)-\mu h(x,y,z)
$$
として
$$
L_x=L_y=L_z=L_{\lambda}=0
$$
$$
g=g_x=g_y=g_z=0
$$
$$
h=h_x=h_y=h_z=0
$$
のどれかを満たす点が極値の候補になります。
極値の候補しか求まらない理由
ラグランジュの未定乗数法はあくまで極値の候補しか求まりません。
公式の導出に記載したとおり、極値の十分条件ではなく必要条件から計算しているからです。
よくある使用方法
極値の候補が求まって嬉しい場面はほとんどありません。最大最小を求めたい場面が大多数です。
条件である$g(x,y)=0$が
- 無限に発散する部分がない
- 閉曲線である(始点と終点がつながっている)
- 連続な関数である
この3つの条件を満たしているとき、ラグランジュの未定乗数法で求められた極値の候補の中に最大最小となる点が必ずあります。
$g(x,y)=0$が円なり楕円なりのときはラグランジュの未定乗数法で最大最小が求められるということです。
まとめ
$g(x,y)=0$の条件下で$f(x,y)$の極値の候補を求めるとき、ラグランジュ定数$\lambda$を用いてラグランジュ関数$L$を以下のように定義します。
$$
L(x,y,\lambda)
=
f(x,y)-\lambda g(x,y)
$$
このとき以下2式のどちらかを満たす点が極値の候補になります。
$$
L_x=L_y=L_{\lambda}=0
\tag{1}
$$
$$
g=g_x=g_y=0
\tag{2}
$$



コメント欄