こんにちはコーヤです。
このページでは余因子の計算方法を3ステップに分けて勉強します。余因子は余因子展開や逆行列の計算に必要です。
余因子の計算3ステップ
余因子の計算方法は3ステップです。
- 符号がプラスかマイナスか調べる
- 小行列の行列式を求める
- 符号と行列式の積を計算する
$$
X
=
\begin{pmatrix}
a & b & c & d\\
e & f & g & h\\
i & j & k & l\\
m & n & o & p
\end{pmatrix}
$$
この行列の1行1列の余因子と2行3列の余因子を例に3ステップで計算してみます。
Step1. 符号がプラスかマイナスか調べる
このステップは簡単です。
行列の1番左上の成分はプラス、その隣はマイナス、その隣はプラスという感じで符号を決めていきます。
$$
X_±
=
\begin{pmatrix}
+ & – & + & -\\
– & + & – & +\\
+ & – & + & -\\
– & + & – & +
\end{pmatrix}
$$
これだけです。
1行1列の余因子の符号はプラス、2行3列の余因子の符号はマイナスです。
Step2. 小行列の行列式を求める
1行1列の余因子を求めるとき、小行列は1行目と1列目を取り除いた行列のことです。
2行3列の余因子を求めるとき、小行列は2行目と3列目を取り除いた行列のことです。
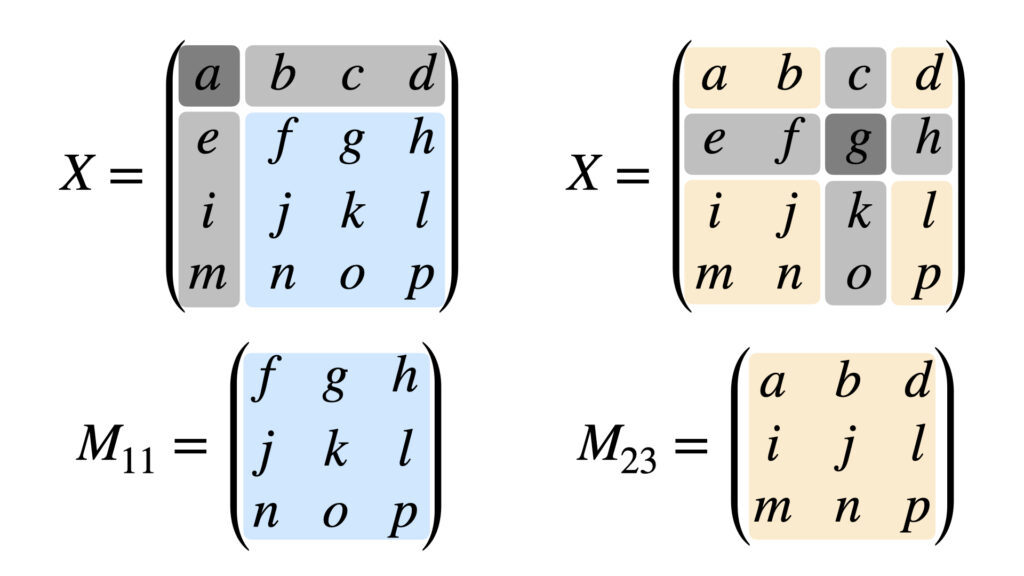
$i$行$j$列を取り除いて小さくした行列は$M_{ij}$と表すことが多いです。
このステップでは小行列の行列式を計算してあげましょう。$\det M_{11}$と$\det M_{23}$の値が求まればOKです。
Step3. 符号と行列式の積を計算する
余因子の値は符号と行列式の積です。
$X_±$の1行1列の符号はプラス、行列式は$\det M_{11}$なので、余因子は$\det M_{11}$です。
$X_±$の2行3列の符号はマイナス、行列式は$\det M_{23}$なので、余因子は$-\det M_{23}$です。
行列$X$の$i$行$j$列の余因子を$X_{ij}$のように表すとすると、今回求めた余因子は
$$
\begin{align}
X_{11} &= \det M_{11}
\\\\
X_{23} &= -\det M_{23}
\end{align}
$$
です。

余因子なんて難しそうな名前がついていますが、小さくした行列の行列式の符号を調整しただけです。
余因子計算の具体例
それでは具体例で余因子を計算してみましょう。
$$
A
=
\begin{pmatrix}
3 & 1 & 2\\
5 & 4 & 1\\
2 & 1 & 3
\end{pmatrix}
$$
この行列の1行1列、1行2列の余因子を求めてみましょう。
Step1. 符号がプラスかマイナスか調べる
プラスマイナスの行列を作ります。
$$
A_±
=
\begin{pmatrix}
+ & – & +\\
– & + & -\\
+ & – & +
\end{pmatrix}
$$
Step2. 小行列の行列式を求める
小さくした行列の行列式を求めます。
$$
\begin{align}
\det M_{11}
&=
\begin{vmatrix}
\cancel{3} & \cancel{1} & \cancel{2}\\
\cancel{5} & 4 & 1\\
\cancel{2} & 1 & 3
\end{vmatrix}
\\\\&=
\begin{vmatrix}
4 & 1\\
1 & 3
\end{vmatrix}
\\\\&=
11
\end{align}
$$
$$
\begin{align}
\det M_{12}
&=
\begin{vmatrix}
\cancel{3} & \cancel{1} & \cancel{2}\\
5 & \cancel{4} & 1\\
2 & \cancel{1} & 3
\end{vmatrix}
\\\\&=
\begin{vmatrix}
5 & 1\\
2 & 3
\end{vmatrix}
\\\\&=
13
\end{align}
$$
Step3. 符号と行列式の積を計算する
$A_±$の1行1列の符号はプラス、行列式は$\det M_{11}=11$なので、1行1列の余因子は$A_{11}=11$です。
$A_±$の1行2列の符号はマイナス、行列式は$\det M_{12}=13$なので、1行2列の余因子は$A_{12}=-13$です。
まとめ
余因子の計算方法は3ステップです。
- 符号がプラスかマイナスか調べる
- 小行列の行列式を求める
- 符号と行列式の積を計算する




コメント欄