こんにちはコーヤです。
このページでは固有値と固有ベクトルの計算方法を勉強します。行列の重要な値なので必ず計算できるようになっておきましょう。
固有値と固有ベクトルの意味
まずは固有値と固有ベクトルの意味だけ確認して、具体的な計算はページ後半で行います。
行列$A$でベクトル$\boldsymbol{v}$を写像するとき、以下の条件を満たす特別な$\boldsymbol{v}$を考えます。
- 写像後に$\boldsymbol{v}$と同方向か逆方向のベクトルになる
- 写像後に長さが変わるのはOK
- $\boldsymbol{v} = 0$は対象外
例えば以下のようなベクトルがこれらの条件を満たします。
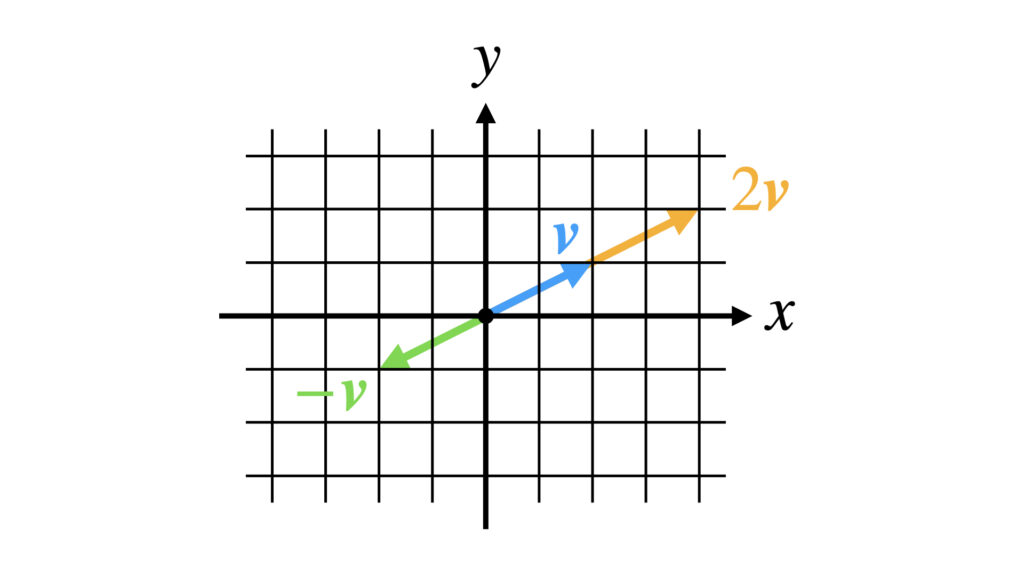
$2\boldsymbol{v}$は同方向で長さが変わったときです。$-\boldsymbol{v}$は逆方向になって長さが変わらなかったときです。他にも$-2\boldsymbol{v}$とか$3\boldsymbol{v}$とか無限にあります。
ベクトル$\boldsymbol{v}$が行列$A$で写像された結果である、というのも考慮して式で表してみると
$$
\begin{align}
A \boldsymbol{v} &= 2\boldsymbol{v}
\\\\
A \boldsymbol{v} &= -\boldsymbol{v}
\end{align}
$$
こうなります。この条件を一般的な式で表します。ベクトルの係数を$\lambda$とすると
$$
A \boldsymbol{v} = \lambda \boldsymbol{v}
$$
となります。
この式が成り立つとき
- $\lambda$を行列$A$の固有値
- $\boldsymbol{v}$を固有値$\lambda$に対する固有ベクトル
と言います。
固有値と固有ベクトルの計算の流れ
固有値、固有ベクトルの条件は
$$
A \boldsymbol{v} = \lambda \boldsymbol{v}
$$
を満たすものでした。
右辺を左辺に移項して
$$
(A-\lambda E) \boldsymbol{v} = 0
$$
となります。単位行列$E$を使って$\lambda$を行列の形で表しているのに注意です。
ここで$(A-\lambda E)$の逆行列を両辺左側からかけてみます。
$$
(A-\lambda E)^{-1}(A-\lambda E) \boldsymbol{v} = (A-\lambda E)^{-1}0\\
$$
これを計算すると$\boldsymbol{v}=0$となってします。
冒頭で紹介したとおり固有ベクトルは$\boldsymbol{v} \neq 0$です。
この矛盾を解消するために、固有ベクトルを求めるときは$(A-\lambda E)$に逆行列が存在しないという設定をしてあげます。
逆行列が存在しないということは行列式が0になるはずなので
$$
\det (A-\lambda E) = 0
$$
を満たす場合にのみ注目して計算を進めていきます。この式を行列$A$の固有方程式といいます。
固有値の計算方法
ここからは具体的な計算方法を見ていきます。行列$A$を以下のようにします。
$$
\begin{pmatrix}
1 & 2 \\
-1 & 4
\end{pmatrix}
$$
固有値$\lambda$が満たす条件はさきほど紹介したように
$$
\det (A-\lambda E) = 0
$$
です。まずは$A-\lambda E$を計算して
$$
\begin{pmatrix}
1 & 2 \\
-1 & 4
\end{pmatrix}
-\begin{pmatrix}
\lambda & 0 \\
0 & \lambda
\end{pmatrix}
=
\begin{pmatrix}
1-\lambda & 2 \\
-1 & 4-\lambda
\end{pmatrix}
$$
これの行列式を計算します。
$$
\begin{align}
\begin{vmatrix}
1-\lambda & 2 \\
-1 & 4-\lambda
\end{vmatrix}
&=
(1-\lambda)(4-\lambda)+2
\\\\&=
\lambda^2-5\lambda+6
\\\\&=
(\lambda-2)(\lambda-3)
\end{align}
$$
これが0になればいいので$\lambda$の値は
$$
\begin{array}{cc}
\lambda_1=2
&
\lambda_2=3
\end{array}
$$
となります。これで固有値が求まりました。
固有ベクトルの計算方法
固有値が求まったら固有ベクトルが計算できます。
$$
(A-\lambda E) \boldsymbol{v} = 0
$$
この式にさっき求めた$\lambda_1=2$と$\lambda_2=3$を代入して計算していきます。
$\lambda_1=2$のときの固有ベクトルを$\boldsymbol{v}_1$として、ベクトルの成分を以下のようにします。
$$
\boldsymbol{v}_1
=
\begin{pmatrix}
x_1\\
y_1
\end{pmatrix}
$$
あとは計算していくだけです。
$$
\begin{align}
(A-\lambda_1 E) \boldsymbol{v}_1
&=
\begin{pmatrix}
1-2 & 2 \\
-1 & 4-2
\end{pmatrix}
\begin{pmatrix}
x_1\\
y_1
\end{pmatrix}
\\\\&=
\begin{pmatrix}
-1 & 2 \\
-1 & 2
\end{pmatrix}
\begin{pmatrix}
x_1\\
y_1
\end{pmatrix}
\end{align}
$$
この計算結果を
$$
(A-\lambda_1 E) \boldsymbol{v}_1 = 0
$$
に代入して
$$
\begin{pmatrix}
-1 & 2 \\
-1 & 2
\end{pmatrix}
\begin{pmatrix}
x_1\\
y_1
\end{pmatrix}
=
0
$$
これは同次連立1次方程式の形になっています。自由度1なので任意定数1個で$\boldsymbol{v}_1$を表現できます。
同次連立1次方程式や自由度が不安な方はご覧ください。
任意定数を$k_1$として
$$
\boldsymbol{v}_1
=
k_1
\begin{pmatrix}
2\\
1
\end{pmatrix}
$$
です。これで固有ベクトルが求まりました。
同様に$\lambda_2=3$のときの固有ベクトル$\boldsymbol{v}_2$も求めていきます。
$$
\boldsymbol{v}_2
=
\begin{pmatrix}
x_2\\
y_2
\end{pmatrix}
$$
任意定数を$k_2$として
$$
\begin{pmatrix}
-2 & 2 \\
-1 & 1
\end{pmatrix}
\begin{pmatrix}
x_2\\
y_2
\end{pmatrix}
=
0
$$
となるので
$$
\boldsymbol{v}_2
=
k_2
\begin{pmatrix}
1\\
1
\end{pmatrix}
$$
です。
以上より固有ベクトルは
$$
\begin{array}{cc}
\boldsymbol{v}_1
=
k_1
\begin{pmatrix}
2\\
1
\end{pmatrix}
&
\boldsymbol{v}_2
=
k_2
\begin{pmatrix}
1\\
1
\end{pmatrix}
\end{array}
$$
となります。
固有ベクトルは
$$
(A-\lambda E) \boldsymbol{v} = 0
$$
を満たすものでした。この式を変形すると
$$
\boldsymbol{v}
\in
\mathrm{Ker}\, (A-\lambda E)
$$
と書くことができます。どちらも同じ意味なので、好きな方で計算してください。
ちなみに、この式に登場する$\mathrm{Ker}\, (A-\lambda E)$を固有値$\lambda$に対する固有空間といい
$$
W(\lambda)
=
\mathrm{Ker}\, (A-\lambda E)
$$
と表します。
固有値と固有ベクトルの検算方法
固有値と固有ベクトルの検算方法です。
かなり簡単に検算できるので、試験中に使ってください。
固有値の検算方法
固有値は以下の2つの性質があります。
- 固有値の和は行列の対角和と一致する
- 固有値の積は行列の行列式と一致する
これらの性質を使って検算ができます。今の例を使って検算してみます。
固有値は$\lambda_1=2,\lambda_2=3$なので和は5、積は6です。
行列の対角和は左上から右下に向かって成分を足していったもので$\mathrm{tr}\, A$と表されます。
$$
\begin{align}
\mathrm{tr}\, A
&=
\begin{pmatrix}
1 & \cancel{2} \\
\cancel{-1} & 4
\end{pmatrix}
\\\\&=
1+4
\\\\&=
5
\end{align}
$$
たしかに固有値の和と一致しました。
次に行列式を求めると
$$
\begin{align}
\det A
&=
\begin{vmatrix}
1 & 2 \\
-1 & 4
\end{vmatrix}
\\\\&=
6
\end{align}
$$
たしかに固有値の積と一致しました。
固有ベクトルの検算方法
固有ベクトルの検算方法はこの式を満たしているかどうか検算すれば大丈夫です。
$$
A \boldsymbol{v} = \lambda \boldsymbol{v}
$$
試しに$\boldsymbol{v}_1$を検算してみます。
$$
\begin{pmatrix}
1 & 2 \\
-1 & 4
\end{pmatrix}
k_1
\begin{pmatrix}
2\\
1
\end{pmatrix}
=
2k_1
\begin{pmatrix}
2\\
1
\end{pmatrix}
$$
長さが2倍の同方向のベクトルになりました。
まとめ
$$
\det (A-\lambda E) = 0
$$
固有方程式を解くと固有値が求まります。
$$
(A-\lambda E) \boldsymbol{v} = 0
$$
この式に固有値を代入すると固有ベクトルが求まります。





コメント欄