面積と曲線の長さの計算方法

こんにちはコーヤです。

このページでは、面積と曲線の長さの計算方法を勉強します。陽関数表示、媒介変数表示、極座標表示の3パターンです。

面積と曲線の長さの公式
面積と曲線の長さの例題
公式の導出
まとめ

面積と曲線の長さの公式

陽関数表示、媒介変数表示、極座標表示の3パターンにおいて、面積 $S$ と曲線の長さ $L$ を以下のように決めます。

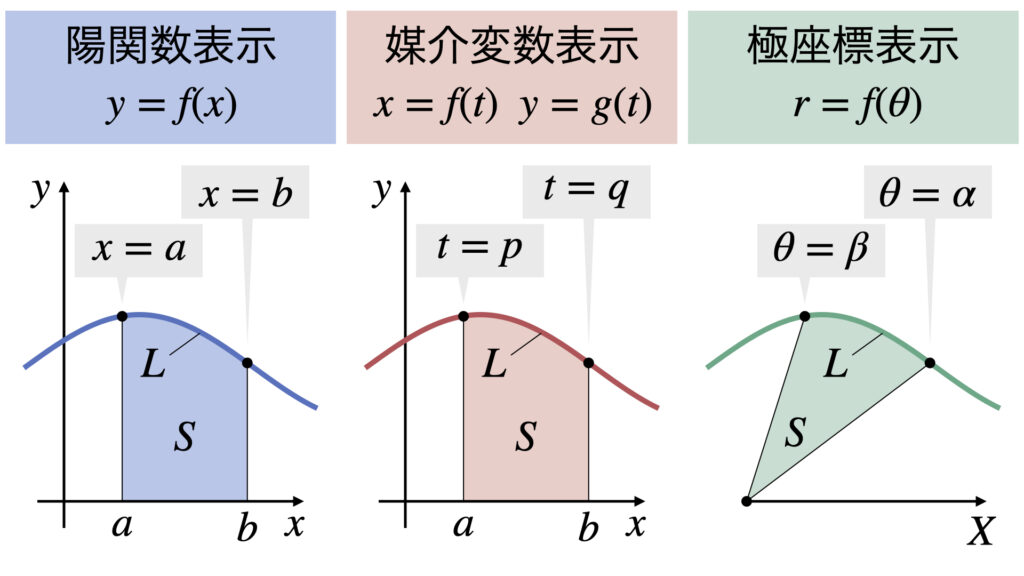
このとき、それぞれの表示形式において面積 $S$ と曲線の長さ $L$ の公式は以下の式です。

陽関数表示の公式

$\begin{aligned} S & = \int_{a}^{b} f (x) d x \\ L & = \int_{a}^{b} \sqrt{1 + f^{'} (x)^{2}} d x \end{aligned}$

媒介変数表示の公式

$\begin{aligned} S & = \int_{p}^{q} f^{'} (t) g (t) d t \\ L & = \int_{p}^{q} \sqrt{f^{'} (t)^{2} + g^{'} (t)^{2}} d t \end{aligned}$

極座標表示の公式

$\begin{aligned} S & = \frac{1}{2} \int_{α}^{β} f (θ)^{2} d θ \\ L & = \int_{α}^{β} \sqrt{f (θ)^{2} + f^{'} (θ)^{2}} d θ \end{aligned}$

それでは例題で計算しましょう。

面積と曲線の長さの例題

陽関数表示の例題

$\begin{array}{cc} y = f (x) = \cosh x & (0 \leq x \leq \log 2) \end{array}$

この関数の面積 $S$ と曲線の長さ $L$ を計算します。

まずは面積 $S$ の計算です。

$\begin{aligned} S & = \int_{0}^{\log 2} f (x) d x \\ = \int_{0}^{\log 2} \cosh x d x \\ = {[\sinh x]}_{0}^{\log 2} \\ = \sinh (\log 2) \\ = \frac{3}{4} \end{aligned}$

次に曲線の長さ $L$ の計算です。

$f^{'} (x) = \sinh x$

より

$\begin{aligned} L & = \int_{0}^{\log 2} \sqrt{1 + f^{'} (x)^{2}} d x \\ = \int_{0}^{\log 2} \sqrt{1 + \sinh^{2} x} d x \\ = \int_{0}^{\log 2} \sqrt{\cosh^{2} x} d x \\ = \int_{0}^{\log 2} | \cosh x | d x \\ = \int_{0}^{\log 2} \cosh x d x \\ = \frac{3}{4} \end{aligned}$

途中の絶対値が出てくる式は、 $0 \leq x \leq \log 2$ の範囲で $\cosh x > 0$ なので絶対値が外れます。

最後の積分計算は面積 $S$ と同じ積分なので計算過程を省略しました。

媒介変数表示の例題

$\begin{array}{cc} \begin{array}{l} x = f (t) = t - \sin t \\ y = g (t) = 1 - \cos t \end{array} & (0 \leq t \leq 2 π) \end{array}$

この関数の面積 $S$ と曲線の長さ $L$ を計算します。サイクロイドと呼ばれる関数です。

まずは面積 $S$ の計算です。

$f^{'} (t) = 1 - \cos t$

より

$\begin{aligned} S & = \int_{0}^{2 π} f^{'} (t) g (t) d t \\ = \int_{0}^{2 π} (1 - \cos t) (1 - \cos t) d t \\ = \int_{0}^{2 π} 1 - 2 \cos t + \cos^{2} t d t \\ = \frac{1}{2} \int_{0}^{2 π} \cos 2 t - 4 \cos t + 3 d t \\ = \frac{1}{2} {[\frac{1}{2} \sin 2 t - 4 \sin t + 3 t]}_{0}^{2 π} \\ = 3 π \end{aligned}$

次に曲線の長さ $L$ の計算です。

$g^{'} (t) = \sin t$

より

$\begin{aligned} L & = \int_{0}^{2 π} \sqrt{f^{'} (t)^{2} + g^{'} (t)^{2}} d t \\ = \int_{0}^{2 π} \sqrt{(1 - \cos t)^{2} + \sin^{2} t} d t \\ = \int_{0}^{2 π} \sqrt{2 - 2 \cos t} d t \\ = \int_{0}^{2 π} \sqrt{4 \sin^{2} \frac{t}{2}} d t \\ = \int_{0}^{2 π} | 2 \sin \frac{t}{2} | d t \\ = \int_{0}^{2 π} 2 \sin \frac{t}{2} d t \\ = {[- 4 \cos \frac{t}{2}]}_{0}^{2 π} \\ = 8 \end{aligned}$

途中の絶対値が出てくる式は、 $0 \leq t \leq 2 π$ の範囲で $\sin \frac{t}{2} > 0$ なので絶対値が外れます。

極座標表示の例題

$\begin{array}{cc} r = f (θ) = 1 + \cos θ & (0 \leq θ \leq π) \end{array}$

この関数の面積 $S$ と曲線の長さ $L$ を計算します。カージオイドと呼ばれる関数です。

まずは面積 $S$ の計算です。

$\begin{aligned} S & = \frac{1}{2} \int_{0}^{π} f (θ)^{2} d θ \\ = \frac{1}{2} \int_{0}^{π} (1 + \cos θ)^{2} d θ \\ = \frac{1}{4} \int_{0}^{π} \cos 2 θ + 4 \cos θ + 3 d θ \\ = \frac{1}{4} {[\frac{1}{2} \sin 2 θ + 4 \sin θ + 3 θ]}_{0}^{π} \\ = \frac{3}{4} π \end{aligned}$

次に曲線の長さ $L$ の計算です。

$f^{'} (θ) = - \sin θ$

より

$\begin{aligned} L & = \int_{0}^{π} \sqrt{f (θ)^{2} + f^{'} (θ)^{2}} d θ \\ = \int_{0}^{π} \sqrt{(1 + \cos θ)^{2} + (- \sin θ)^{2}} d θ \\ = \int_{0}^{π} \sqrt{2 + 2 \cos θ} d θ \\ = \int_{0}^{π} \sqrt{4 \cos^{2} \frac{θ}{2}} d θ \\ = \int_{0}^{π} | 2 \cos \frac{θ}{2} | d θ \\ = \int_{0}^{π} 2 \cos \frac{θ}{2} d θ \\ = {[4 \sin \frac{θ}{2}]}_{0}^{π} \\ = 4 \end{aligned}$

途中の絶対値が出てくる式は、 $0 \leq θ \leq π$ の範囲で $\cos \frac{θ}{2} \geq 0$ なので絶対値が外れます。

公式の導出

それぞれの公式の導出を行います。

陽関数表示の公式の導出

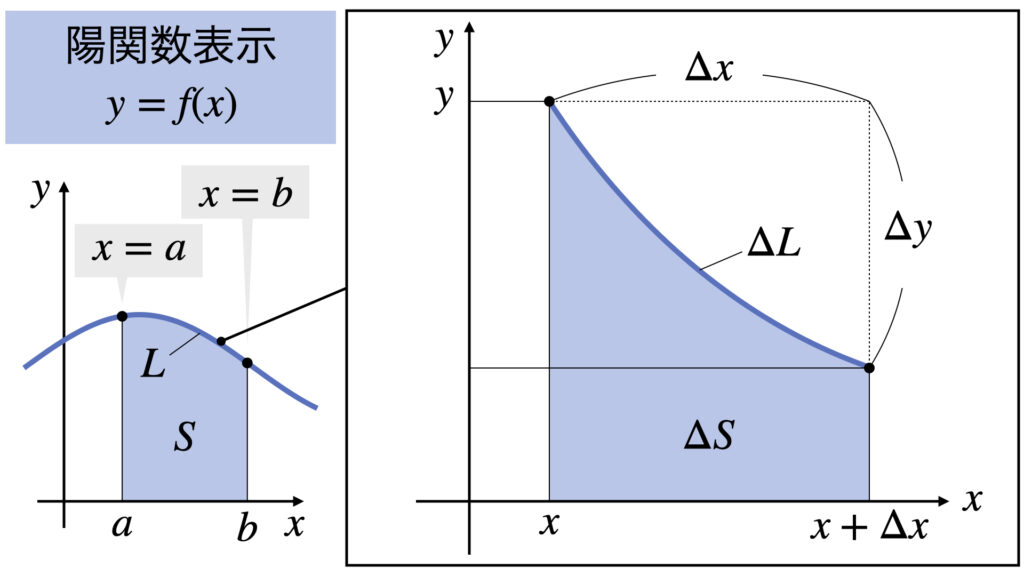
まず面積 $S$ の公式を導出します。

直接 $Δ S$ を計算することはできないので、はさみうちで評価します。

$Δ S$ より小さい面積として、幅 $Δ x$ で高さ $y - Δ y$ の長方形があります。

$Δ S$ より大きい面積として、幅 $Δ x$ で高さ $y$ の長方形があります。

よって

$(y - Δ y) Δ x < Δ S < y Δ x$

とはさみうちができます。不等式を整理して

$y - Δ y < \frac{Δ S}{Δ x} < y$

ここで $Δ x \to 0$ のとき $Δ y \to 0$ なので

$y < \frac{d S}{d x} < y$

となります。よって

$\frac{d S}{d x} = y$

両辺を $a \leq x \leq b$ の範囲の $x$ で積分して

$S = \int_{a}^{b} y d x$

となります。

次に曲線の長さ $L$ の公式を導出します。

$Δ L$ を直線だと近似して、三平方の定理より

$\begin{aligned} Δ L & ≃ \sqrt{(Δ x)^{2} + (Δ y)^{2}} \\ = \sqrt{1 + {(\frac{Δ y}{Δ x})}^{2}} Δ x \end{aligned}$

$Δ x$ を移項して

$\frac{Δ L}{Δ x} ≃ \sqrt{1 + {(\frac{Δ y}{Δ x})}^{2}}$

ここで $Δ x \to 0$ のとき

$\frac{d L}{d x} = \sqrt{1 + {(\frac{d y}{d x})}^{2}}$

両辺を $a \leq x \leq b$ の範囲の $x$ で積分して

$L = \int_{a}^{b} \sqrt{1 + {(\frac{d y}{d x})}^{2}} d x$

となります。

媒介変数表示の公式の導出

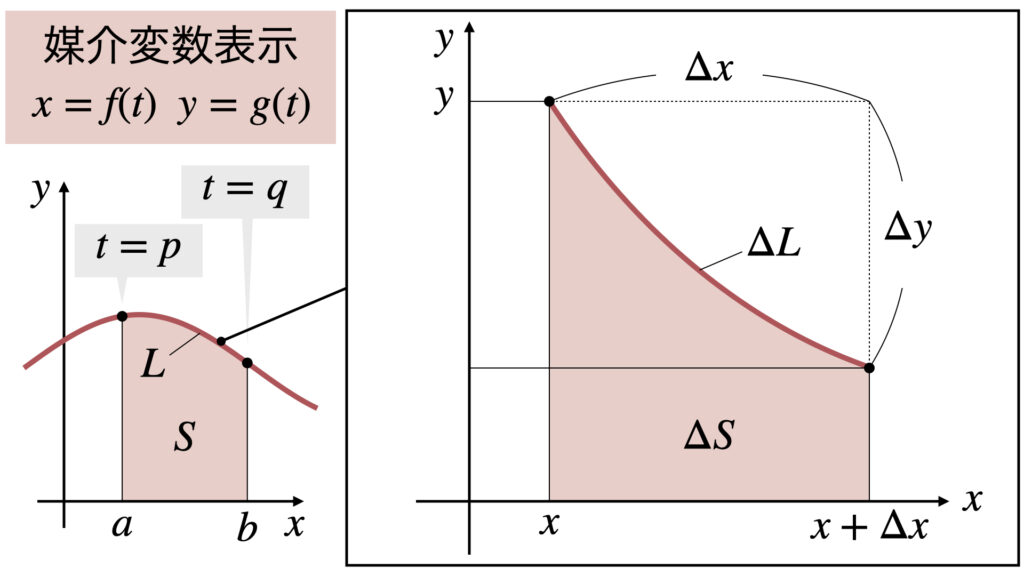
面積 $S$ の公式は陽関数の公式の変数を $x = f (t)$ と置換すれば求まります。

$\begin{aligned} S & = \int_{a}^{b} y d x \\ = \int_{p}^{q} y \frac{d x}{d t} d t \end{aligned}$

曲線の長さ $L$ の公式も陽関数のときと同じような計算です。

三平方の定理より

$\begin{aligned} Δ L & ≃ \sqrt{(Δ x)^{2} + (Δ y)^{2}} \\ = \sqrt{{(\frac{Δ x}{Δ t})}^{2} + {(\frac{Δ y}{Δ t})}^{2}} Δ t \end{aligned}$

$Δ t$ を移項して

$\frac{Δ L}{Δ t} ≃ \sqrt{{(\frac{Δ x}{Δ t})}^{2} + {(\frac{Δ y}{Δ t})}^{2}}$

ここで $Δ t \to 0$ のとき

$\frac{d L}{d t} = \sqrt{{(\frac{d x}{d t})}^{2} + {(\frac{d y}{d t})}^{2}}$

両辺を $p \leq t \leq q$ の範囲の $t$ で積分して

$L = \int_{p}^{q} \sqrt{{(\frac{d x}{d t})}^{2} + {(\frac{d y}{d t})}^{2}} d t$

となります。

極座標表示の公式の導出

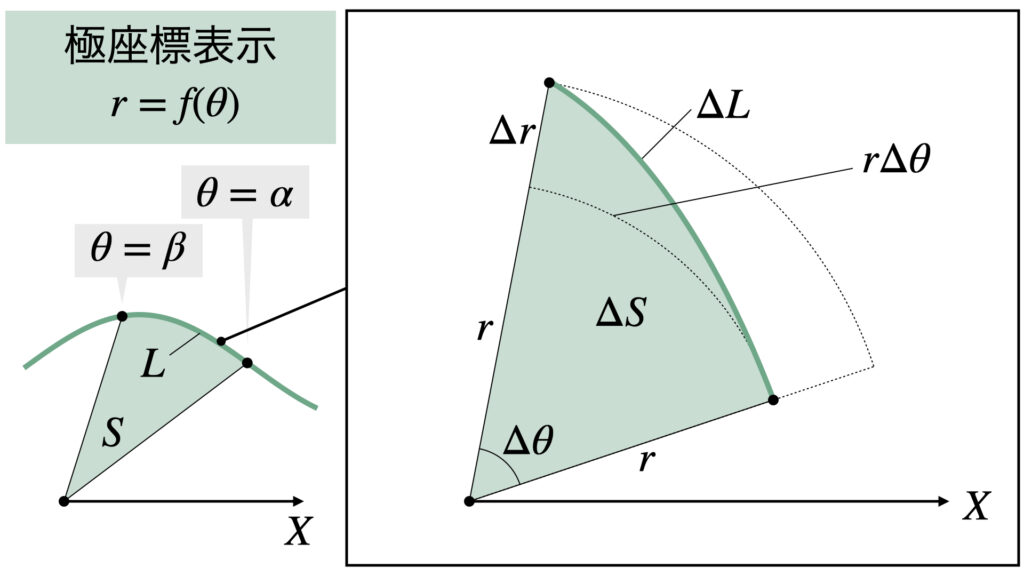
まず面積 $S$ の公式を導出します。

直接 $Δ S$ を計算することはできないので、はさみうちで評価します。

$Δ S$ より小さい面積として、半径 $r$ で中心角 $Δ θ$ の扇形があります。

$Δ S$ より大きい面積として、半径 $r + Δ r$ で中心角 $Δ θ$ の扇形があります。

よって

$r^{2} π \frac{Δ θ}{2 π} < Δ S < (r + Δ r)^{2} π \frac{Δ θ}{2 π}$

とはさみうちができます。不等式を整理して

$\frac{1}{2} r^{2} < \frac{Δ S}{Δ θ} < \frac{1}{2} (r + Δ r)^{2}$

ここで $Δ θ \to 0$ のとき $Δ r \to 0$ なので

$\frac{1}{2} r^{2} < \frac{d S}{d θ} < \frac{1}{2} r^{2}$

となります。よって

$\frac{d S}{d θ} = \frac{1}{2} r^{2}$

両辺を $α \leq θ \leq β$ の範囲の $θ$ で積分して

$S = \frac{1}{2} \int_{α}^{β} r^{2} d θ$

となります。

次に曲線の長さ $L$ の公式を導出します。陽関数のときと同じように三平方の定理で近似します。

図の $Δ L$ と $Δ r$ と点線で示す半径 $r$ で中心角 $Δ θ$ の扇形の弧の3辺で三角形を作ります。

半径 $r$ で中心角 $Δ θ$ の扇形の弧の長さは

$2 r \frac{Δ θ}{2 π} π = r Δ θ$

です。これを使って三平方の定理より

$\begin{aligned} Δ L & ≃ \sqrt{(r Δ θ)^{2} + (Δ r)^{2}} \\ = \sqrt{r^{2} + {(\frac{Δ r}{Δ θ})}^{2}} Δ θ \end{aligned}$

$Δ θ$ を移項して

$\frac{Δ L}{Δ θ} ≃ \sqrt{r^{2} + {(\frac{Δ r}{Δ θ})}^{2}}$

ここで $Δ θ \to 0$ のとき

$\frac{d L}{d θ} = \sqrt{r^{2} + {(\frac{d r}{d θ})}^{2}}$

両辺を $α \leq θ \leq β$ の範囲の $θ$ で積分して

$L = \int_{α}^{β} \sqrt{r^{2} + {(\frac{d r}{d θ})}^{2}} d θ$

となります。

まとめ

陽関数表示、媒介変数表示、極座標表示の3パターンにおいて、面積 $S$ と曲線の長さ $L$ を以下のように決めます。

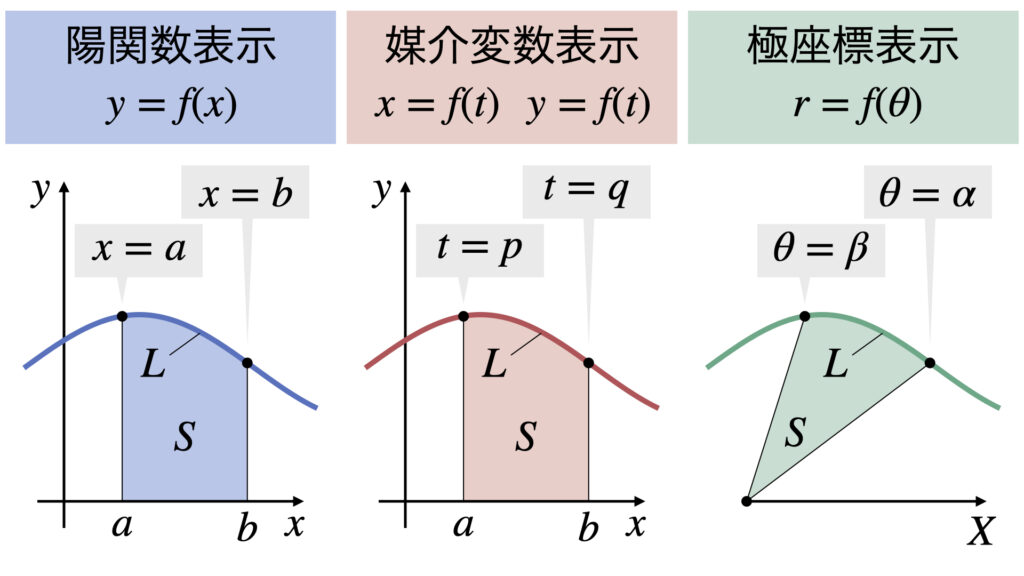
このとき、それぞれの表示形式において面積 $S$ と曲線の長さ $L$ の公式は以下の式です。

陽関数表示

$\begin{aligned} S & = \int_{a}^{b} f (x) d x \\ L & = \int_{a}^{b} \sqrt{1 + f^{'} (x)^{2}} d x \end{aligned}$

媒介変数表示

$\begin{aligned} S & = \int_{p}^{q} f^{'} (t) g (t) d t \\ L & = \int_{p}^{q} \sqrt{f^{'} (t)^{2} + g^{'} (t)^{2}} d t \end{aligned}$

極座標表示

$\begin{aligned} S & = \frac{1}{2} \int_{α}^{β} f (θ)^{2} d θ \\ L & = \int_{α}^{β} \sqrt{f (θ)^{2} + f^{'} (θ)^{2}} d θ \end{aligned}$

回転体の体積と表面積の計算方法

回転体の体積と表面積の計算方法を勉強します。陽関数表示、媒介変数表示、極座標表示の3パターンです。

知っていると便利な積分のテクニック

知っていると便利な積分のテクニックとしてワイエルシュトラス置換、キングプロパティ、矢印部分積分（瞬間部分積分）の3つを勉強します。

面積と曲線の長さの計算方法

面積と曲線の長さの公式

陽関数表示の公式

媒介変数表示の公式

極座標表示の公式

面積と曲線の長さの例題

陽関数表示の例題

媒介変数表示の例題

極座標表示の例題

公式の導出

陽関数表示の公式の導出

媒介変数表示の公式の導出

極座標表示の公式の導出

まとめ

陽関数表示

媒介変数表示

極座標表示

次のページ

前のページ

目次

コメント欄