こんにちはコーヤです。
このページでは、多変数関数に含まれる変数すべてに注目して微分する、全微分の意味と計算方法を勉強します。
偏微分と全微分の違い
偏微分と比べながら全微分の意味を確認します。
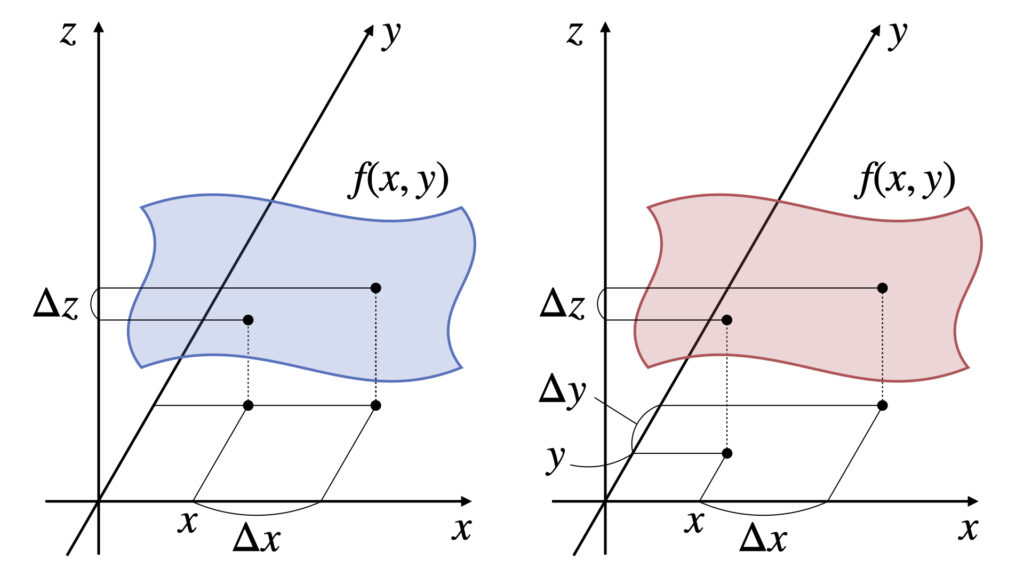
左側が偏微分のイメージ、右側が全微分のイメージです。
偏微分の変化量
$x$が$\Delta x$だけ変化した時の$z$の変化量$\Delta z$は以下の式で表されます。
$$
\Delta z
=
f(x+\Delta x,y)-f(x,y)
$$
全微分の変化量
$x$が$\Delta x$だけ、$y$が$\Delta y$だけ変化した時の$z$の変化量$\Delta z$は以下の式で表されます。
$$
\Delta z
=
f(x+\Delta x,y+\Delta y)-f(x,y)
$$
偏微分は1つの変数に注目して微分しましたが、全微分では全ての変数に注目して微分します。
全微分の条件と公式
全微分可能となる条件は以下の式が成り立つことです。
$$
\displaystyle\lim_{(\Delta x \Delta y)\to (0,0)}
\displaystyle\frac{f(x+\Delta x,y+\Delta y)
-\left\{
f(x,y)+f_x(x,y) \Delta x + f_y(x,y) \Delta y
\right\}}{\sqrt{(\Delta x)^2+(\Delta y)^2}}
=
0
$$
このとき全微分は以下のように表されます。
$$
df=f_x(x,y)dx+f_y(x,y)dy
$$
条件と公式だけ見ても意味が分からないので、この条件と公式の導出を行います。
全微分の導出
曲面$z=f(x,y)$を平面で近似できるか計算します。
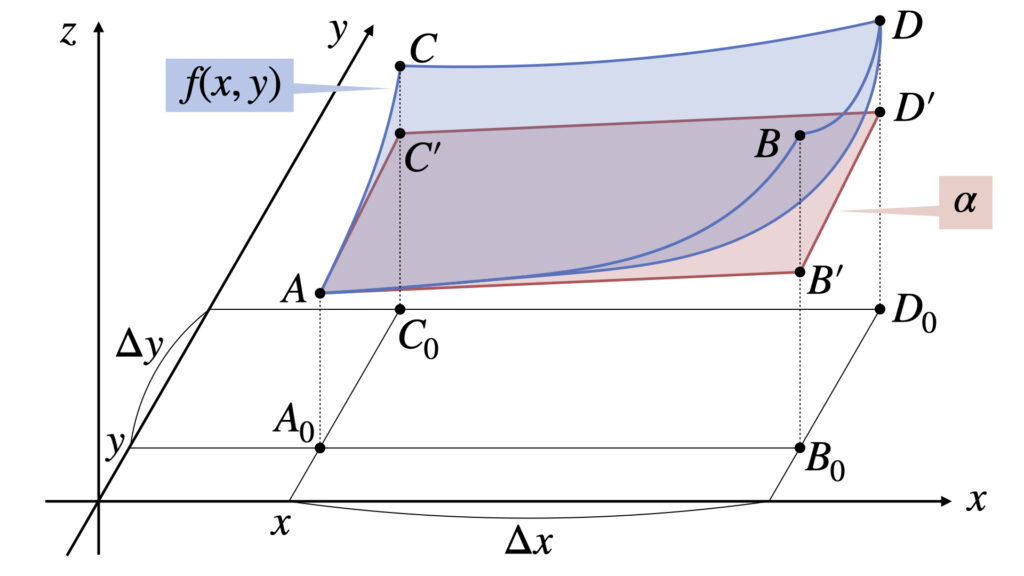
図の曲面が$f(x,y)$、平面$\alpha$が点$A$における近似平面を表しています。
点$A_0,B_0,C_0,D_0$は$xy$平面上の点で、それぞれ座標は以下のようにします。
$$
\begin{align}
A_0 &= (x,y,0)
\\\\
B_0 &= (x+\Delta x,y,0)
\\\\
C_0 &= (x,y+\Delta y,0)
\\\\
D_0 &= (x+\Delta x,y+\Delta y,0)
\end{align}
$$
点$A_0B_0$間の距離は$\Delta x$で、点$A_0C_0$間の距離は$\Delta y$です。
曲面$f(x,y)$は点$ABCD$で表し、近似平面$\alpha$は点$AB’C’D’$で表します。
ここで近似平面$\alpha$の点$B’$と点$C’$の位置は、曲線$AB$の点$A$での接線が直線$AB’$となるように、曲線$AC$の点$A$での接線が直線$AC’$となるようにします。
次に、この3次元の図を3方向から見ていきます。$ABA_0B_0$の面、$ACA_0C_0$の面、$ADA_0D_0$の面の3種類を以下に表します。
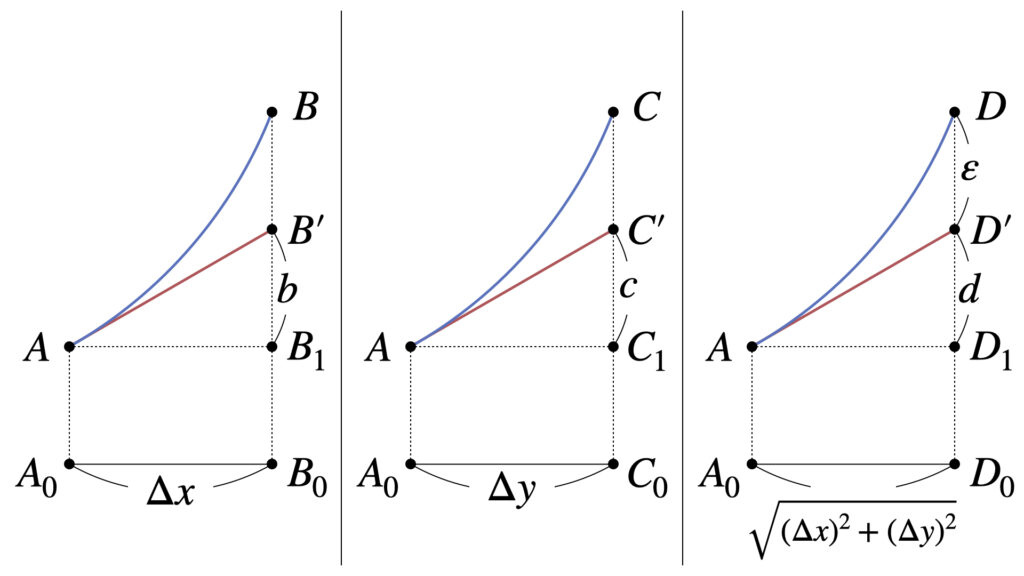
図左側の$ABA_0B_0$の面について考えます。
新たな点$B_1$を図のように設定します。
点$A_0B_0$間の距離は$\Delta x$なので、点$AB_1$間の距離も$\Delta x$です。
直線$AB’$の傾きは曲線$AB$の接線なので傾き$f_x(x,y)$です。
したがって点$B’B_1$間の距離$b$は、傾き$f_x(x,y)$の直線が$\Delta x$だけ変化したときの変化量なので
$$
b
=
f_x(x,y) \Delta x
$$
と表すことができます。
図中央の$ACA_0C_0$の面についても同様の計算です。点$C’C_1$間の距離$c$は以下のように表されます。
$$
c
=
f_y(x,y) \Delta y
$$
最後に図右側の$ADA_0D_0$の面です。
点$D’D_1$間の距離$d$は$AB’C’D’$が平面であることを利用して
$$
\begin{align}
d
&=
b+c
\\\\&=
f_x(x,y) \Delta x + f_y(x,y) \Delta y
\end{align}
$$
となります。
次に点$DD’$間の距離を$\varepsilon(x,y)$とします。
点$D$の$z$座標は$f(x+\Delta x,y+\Delta y)$で、点$D’$の$z$座標は点$A$の$z$座標$f(x,y)$に距離$d$を足したものです。
したがって$\varepsilon(x,y)$は
$$
\varepsilon(x,y)
=
f(x+\Delta x,y+\Delta y)
-\left\{
f(x,y)+f_x \Delta x + f_y \Delta y
\right\}
$$
となります。
これで曲面$f(x,y)$と平面$\alpha$の位置関係が分かりました。
曲面$f(x,y)$を平面$\alpha$で近似する計算をしましたが、点$DD’$間の距離$\varepsilon(x,y)$が曲面と近似平面の誤差となっています。
この誤差$\varepsilon(x,y)$が無視できるほど小さければ近似成功です。
ここで$(\Delta x,\Delta y) \to (0,0)$のとき、点$A_0D_0$間も0になります。点$A_0D_0$間が0になるより速く$\varepsilon(x,y)$が0になってくれれば、誤差は無視できると考えられます。
この条件を式で表すと
$$
\displaystyle\lim_{(\Delta x \Delta y)\to (0,0)}
\displaystyle\frac{\varepsilon(x,y)}{\sqrt{(\Delta x)^2+(\Delta y)^2}}
=
0
$$
となります。これが全微分可能となる条件です。
この条件を満たす場合の点$AD$間の$z$座標の差$\Delta z$を計算しましょう。今$\Delta z$は
$$
\begin{align}
\Delta z
&=
d+\varepsilon(x,y)
\\\\&=
f_x(x,y) \Delta x + f_y(x,y) \Delta y + \varepsilon(x,y)
\end{align}
$$
と表すことができます。両辺を$\sqrt{{(\Delta x)^2+(\Delta y)^2}}$で割って
$$
\displaystyle\frac{\Delta z}{\sqrt{{(\Delta x)^2+(\Delta y)^2}}}
=
f_x(x,y)\displaystyle\frac{\Delta x}{\sqrt{{(\Delta x)^2+(\Delta y)^2}}}
+
f_y(x,y)\displaystyle\frac{\Delta y}{\sqrt{{(\Delta x)^2+(\Delta y)^2}}}
+
\displaystyle\frac{\varepsilon(x,y)}{\sqrt{{(\Delta x)^2+(\Delta y)^2}}}
$$
ここで$(\Delta x,\Delta y) \to (0,0)$とすると、条件より$\varepsilon(x,y)$の項は無視できるので
$$
\displaystyle\frac{dz}{\sqrt{{(dx)^2+(dy)^2}}}
=
f_x(x,y)\displaystyle\frac{dx}{\sqrt{{(dx)^2+(dy)^2}}}
+
f_y(x,y)\displaystyle\frac{dy}{\sqrt{{(dx)^2+(dy)^2}}}
$$
両辺$\sqrt{{(dx)^2+(dy)^2}}$をかけて
$$
dz=f_x(x,y)dx+f_y(x,y)dy
$$
となります。これで条件と公式の導出が終わりました。
全微分計算の例題
それでは例題2つで全微分の計算をしてみましょう。
全微分可能かどうか判定し、その後全微分を求めます。
例題1
$$
f(x,y)
=
x^2+y^2
$$
全微分可能かどうか確かめます。
$$
\begin{align}
f_x(x,y) &= 2x
\\\\
f_y(x,y) &= 2y
\end{align}
$$
より誤差$\varepsilon(x,y)$は
$$
\begin{align}
\varepsilon(x,y)
&=
f(x+\Delta x,y+\Delta y)
-\left\{
f(x,y)+f_x(x,y) \Delta x + f_y(x,y) \Delta y
\right\}
\\\\&=
(x+\Delta x)^2+(y+\Delta y)^2
-\left\{
x^2+y^2+2x\Delta x +2y\Delta y
\right\}
\\\\&=
(\Delta x)^2+(\Delta y)^2
\end{align}
$$
となります。これを全微分の条件式に代入して
$$
\begin{align}
\displaystyle\lim_{(\Delta x \Delta y)\to (0,0)}
\displaystyle\frac{\varepsilon(x,y)}{\sqrt{(\Delta x)^2+(\Delta y)^2}}
&=
\displaystyle\lim_{(\Delta x \Delta y)\to (0,0)}
\displaystyle\frac{(\Delta x)^2+(\Delta y)^2}{\sqrt{(\Delta x)^2+(\Delta y)^2}}
\\\\&=
\displaystyle\lim_{(\Delta x \Delta y)\to (0,0)}
\sqrt{(\Delta x)^2+(\Delta y)^2}
\\\\&=
0
\end{align}
$$
となるので$f(x,y)$は全微分可能です。よって全微分は
$$
\begin{align}
df
&=
f_x(x,y)dx+f_y(x,y)dy
\\\\&=
2xdx+2ydy
\end{align}
$$
となります。
例題2
$$
f(x,y)
=
xy
$$
全微分可能かどうか確かめます。
$$
\begin{align}
f_x(x,y) &= y
\\\\
f_y(x,y) &= x
\end{align}
$$
より誤差$\varepsilon(x,y)$は
$$
\begin{align}
\varepsilon(x,y)
&=
f(x+\Delta x,y+\Delta y)
-\left\{
f(x,y)+f_x(x,y) \Delta x + f_y(x,y) \Delta y
\right\}
\\\\&=
(x+\Delta x)(y+\Delta y)
-\left\{
xy+y\Delta x+x\Delta y
\right\}
\\\\&=
\Delta x\Delta y
\end{align}
$$
となります。これを全微分の条件式に代入して
$$
\displaystyle\lim_{(\Delta x \Delta y)\to (0,0)}
\displaystyle\frac{\varepsilon(x,y)}{\sqrt{(\Delta x)^2+(\Delta y)^2}}
=
\displaystyle\lim_{(\Delta x \Delta y)\to (0,0)}
\displaystyle\frac{\Delta x\Delta y}{\sqrt{(\Delta x)^2+(\Delta y)^2}}
$$
このままだと計算できないので
$$
\begin{align}
\Delta x &= r\cos\theta
\\\\
\Delta y &= r\sin\theta
\end{align}
$$
として$r\to 0$の極限に変換します。
$$
\begin{align}
\displaystyle\lim_{(\Delta x \Delta y)\to (0,0)}
\displaystyle\frac{\Delta x\Delta y}{\sqrt{(\Delta x)^2+(\Delta y)^2}}
&=
\displaystyle\lim_{r\to 0}
\displaystyle\frac{r^2\cos\theta\sin\theta}{r}
\\\\&=
\displaystyle\lim_{r\to 0}
r\cos\theta\sin\theta
\\\\&=
0
\end{align}
$$
となるので$f(x,y)$は全微分可能です。よって全微分は
$$
\begin{align}
df
&=
f_x(x,y)dx+f_y(x,y)dy
\\\\&=
ydx+xdy
\end{align}
$$
となります。
全微分の変数変換
関数$f(x,y)$の$x$と$y$が、他の関数で表されている場合の微分を考えます。
1変数で置換する場合
変数$t$を用いて$x,y$が
$$
\begin{align}
x&= x(t)
\\\\
y &= y(t)
\end{align}
$$
と表される場合、関数$f(x,y)$を$t$で微分すると
$$
\begin{align}
\displaystyle\frac{df}{dt}
&=
\displaystyle\frac{f_x(x,y)dx+f_y(x,y)dy}{dt}
\\\\&=
f_x(x,y)\displaystyle\frac{dx}{dt}+f_y(x,y)\displaystyle\frac{dy}{dt}
\\\\&=
\displaystyle\frac{\partial f}{\partial x}\displaystyle\frac{dx}{dt}+\displaystyle\frac{\partial f}{\partial y}\displaystyle\frac{dy}{dt}
\end{align}
$$
となります。
例えば
$$
\begin{array}{cc|cc}
f(x,y) = xy
&&&
\begin{array}{l}
x = t^3
\\
y = \sin t
\end{array}
\end{array}
$$
この関数を$t$で微分すると
$$
\begin{align}
\displaystyle\frac{df}{dt}
&=
\displaystyle\frac{\partial f}{\partial x}\displaystyle\frac{dx}{dt}+\displaystyle\frac{\partial f}{\partial y}\displaystyle\frac{dy}{dt}
\\\\&=
y \cdot 3t^2 + x \cdot \cos t
\\\\&=
\sin t \cdot 3t^2 + t^3 \cdot \cos t
\\\\&=
3t^2\sin t+t^3\cos t
\end{align}
$$
となります。
2変数で置換する場合
変数$u,v$を用いて$x,y$が
$$
\begin{align}
x&= x(u,v)
\\\\
y &= y(u,v)
\end{align}
$$
と表される場合、関数$f(x,y)$を$u$と$v$でそれぞれ微分すると
$$
\begin{align}
\displaystyle\frac{\partial f}{\partial u}
&=
\displaystyle\frac{f_x(x,y)dx+f_y(x,y)dy}{\partial u}
\\\\&=
f_x(x,y)\displaystyle\frac{\partial x}{\partial u}+f_y(x,y)\displaystyle\frac{\partial y}{\partial u}
\\\\&=
\displaystyle\frac{\partial f}{\partial x}\displaystyle\frac{\partial x}{\partial u}+\displaystyle\frac{\partial f}{\partial y}\displaystyle\frac{\partial y}{\partial u}
\end{align}
$$
$$
\begin{align}
\displaystyle\frac{\partial f}{\partial v}
&=
\displaystyle\frac{f_x(x,y)dx+f_y(x,y)dy}{\partial v}
\\\\&=
f_x(x,y)\displaystyle\frac{\partial x}{\partial v}+f_y(x,y)\displaystyle\frac{\partial y}{\partial v}
\\\\&=
\displaystyle\frac{\partial f}{\partial x}\displaystyle\frac{\partial x}{\partial v}+\displaystyle\frac{\partial f}{\partial y}\displaystyle\frac{\partial y}{\partial v}
\end{align}
$$
となります。
例えば
$$
\begin{array}{cc|cc}
f(x,y) = xy
&&&
\begin{array}{l}
x = u+v
\\
y = uv
\end{array}
\end{array}
$$
この関数を$u$と$v$でそれぞれ微分すると
$$
\begin{align}
\displaystyle\frac{\partial f}{\partial u}
&=
\displaystyle\frac{\partial f}{\partial x}\displaystyle\frac{\partial x}{\partial u}+\displaystyle\frac{\partial f}{\partial y}\displaystyle\frac{\partial y}{\partial u}
\\\\&=
y \cdot 1 + x \cdot v
\\\\&=
uv \cdot 1 + (u+v) \cdot v
\\\\&=
2uv+v^2
\end{align}
$$
$$
\begin{align}
\displaystyle\frac{\partial f}{\partial v}
&=
\displaystyle\frac{\partial f}{\partial x}\displaystyle\frac{\partial x}{\partial v}+\displaystyle\frac{\partial f}{\partial y}\displaystyle\frac{\partial y}{\partial v}
\\\\&=
y \cdot 1 + x \cdot u
\\\\&=
uv \cdot 1 + (u+v) \cdot u
\\\\&=
2uv+u^2
\end{align}
$$
となります。
まとめ
全微分は多変数関数に含まれる全ての変数に注目して微分します。

全微分可能となる条件は以下の式が成り立つことです。
$$
\displaystyle\lim_{(\Delta x \Delta y)\to (0,0)}
\displaystyle\frac{f(x+\Delta x,y+\Delta y)
-\left\{
f(x,y)+f_x \Delta x + f_y \Delta y
\right\}}{\sqrt{(\Delta x)^2+(\Delta y)^2}}
=
0
$$
このとき全微分は以下のように表されます。
$$
df=f_xdx+f_ydy
$$




コメント欄