こんにちはコーヤです。
このページでは、2変数関数の極値の計算方法を勉強します。2変数関数では極値に似た鞍点という点が存在し、線形代数の知識を使うと極値と鞍点を判定できます。
停留点の条件
2変数関数$f(x,y)$が点$(a,b)$で極値を取る必要条件は、1変数関数のときと同様に1階導関数を用いて
$$
f_x(a,b)=f_y(a,b)=0
$$
となり、これを満たす点を停留点といいます。
停留点には極大値、極小値、鞍点、それ以外の4種類の点があります。
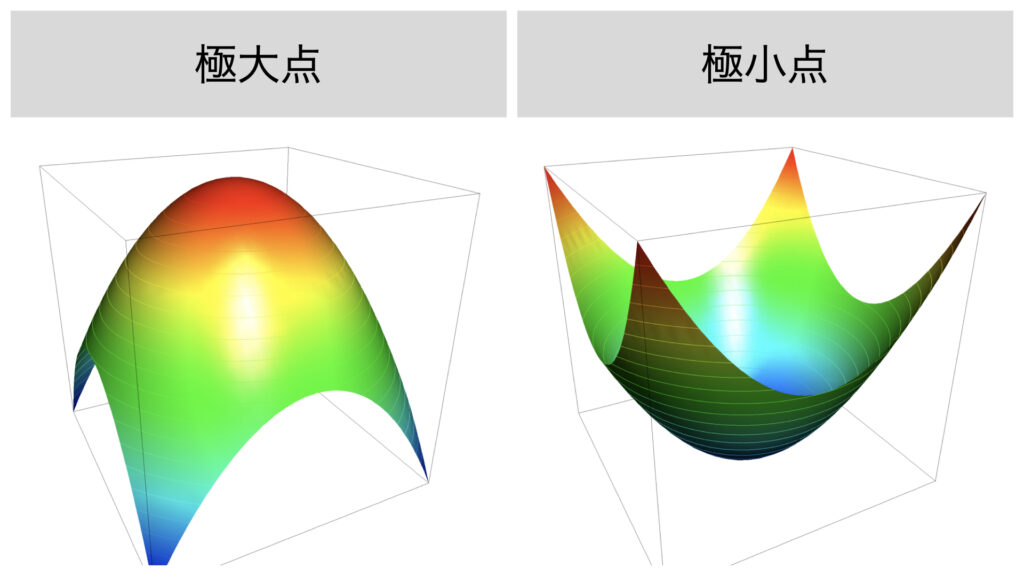
極大値と極小値は1変数関数のときと同じイメージです。どの方向から見ても極値の点を境目に1階導関数の符号が変化します。
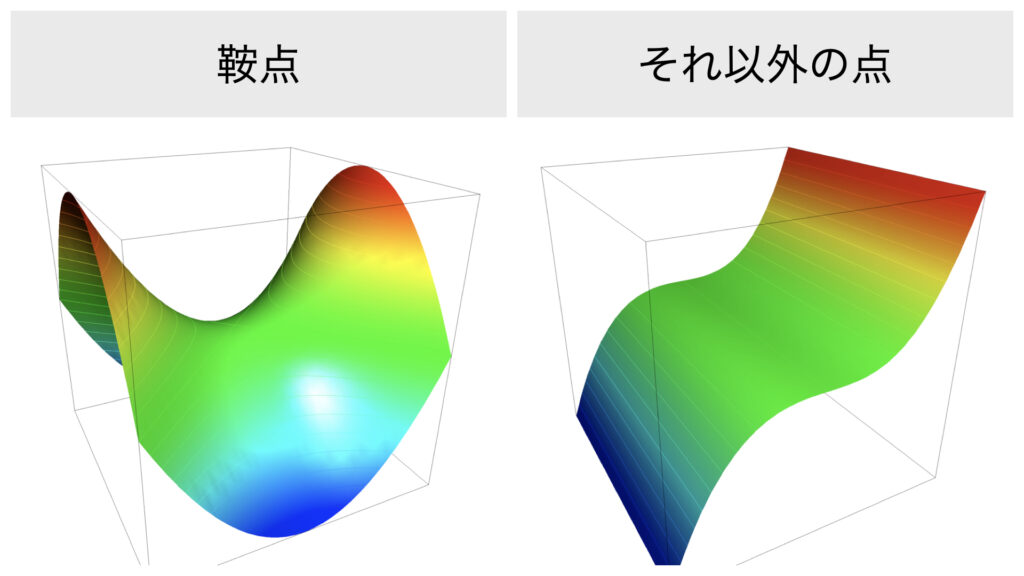
鞍点は1変数関数のときは登場しませんでした。ある方向から見ると極大値っぽく見えても別の方向から見ると極小値っぽく見える点のことです。
それ以外の点について、1変数関数$y=x^3$の$x=0$の点をイメージすれば伝わるかと思います。1階導関数の値は0になるものの、極値とも鞍点とも言えない点があります。
停留点の判定方法
極大値、極小値、鞍点の判定方法は、以下のヘッセ行列$H$を用います。
$$
H
=
\begin{pmatrix}
f_{xx}(a,b) & f_{xy}(a,b) \\
f_{yx}(a,b) & f_{yy}(a,b)
\end{pmatrix}
$$
この行列式$\det H$が
- $\det H >0$なら極値
- $f_{xx}(a,b)>0$もしくは$f_{yy}(a,b)>0$なら極小値
- $f_{xx}(a,b)<0$もしくは$f_{yy}(a,b)<0$なら極大値
- $\det H <0$なら鞍点
- $\det H =0$のときは判定不能
となります。

$\det H$のことを「ヘッセシアン」といいます。
極値と鞍点の計算3ステップ
それでは極値と鞍点の計算の具体例を見ていきます。3ステップです。
- 停留点を求める
- ヘッセシアンを求める
- 極値か鞍点か判定する
以下の2変数関数$f(x,y)$を計算します。
$$
f(x,y)
=
3x^2-6xy+y^3
$$
ステップ1. 停留点を求める
1階偏導関数を計算して
$$
\begin{align}
f_x(x,y)
&=
6x-6y
\\\\
f_y(x,y)
&=
-6x+3y^2
\end{align}
$$
となります。
$$
f_x(x,y)
=
6x-6y
=
0
$$
より$x=y$です。これを$f_y(x,y)=0$に代入して
$$
\begin{align}
0
&=
f_y(x,y)
\\\\&=
-6x+3y^2
\\\\&=
-6y+3y^2
\\\\&=
3y(y-2)
\end{align}
$$
これより$y=0,2$となります。
$x=y$の条件と合わせて、停留点は$(x,y)=(0,0),$$(2,2)$の2点です。
ステップ2. ヘッセシアンを求める
2階偏導関数を計算して
$$
\begin{align}
f_{xx}(x,y)
&=
6
\\\\
f_{xy}(x,y)
&=
-6
\\\\
f_{yx}(x,y)
&=
-6
\\\\
f_{yy}(x,y)
&=
6y
\end{align}
$$
となります。ヘッセシアンは
$$
\begin{align}
\det H
&=
\begin{vmatrix}
f_{xx}(x,y) & f_{xy}(x,y) \\
f_{yx}(x,y) & f_{yy}(x,y)
\end{vmatrix}
\\\\&=
\begin{vmatrix}
6 & -6 \\
-6 & 6y
\end{vmatrix}
\\\\&=
36(y-1)
\end{align}
$$
となります。
ステップ3. 極値か鞍点か判定する
停留点$(x,y)=(0,0),$$(2,2)$の2点それぞれで判定します。
$(x,y)=(0,0)$のとき、ヘッセシアンは
$$
\begin{align}
\det H
&=
36(y-1)
\\\\&=
36(0-1)
\\\\&=
-36
\end{align}
$$
$\det H <0$なので鞍点となります。
$(x,y)=(2,2)$のとき、ヘッセシアンは
$$
\begin{align}
\det H
&=
36(y-1)
\\\\&=
36(2-1)
\\\\&=
36
\end{align}
$$
$\det H >0$なので極値となります。$f_{xx}(2,2)=6>0$なので極小値です。
判定方法の導出
ヘッセシアンで極値や鞍点が判定でき、$f_{xx}$や$f_{yy}$の符号で極大極小の判定ができる理由について考えます。
点$(a,b)$が停留点となるとき、$f(a,b)$付近で$f(x,y)$を切ったときの断面図を考えると
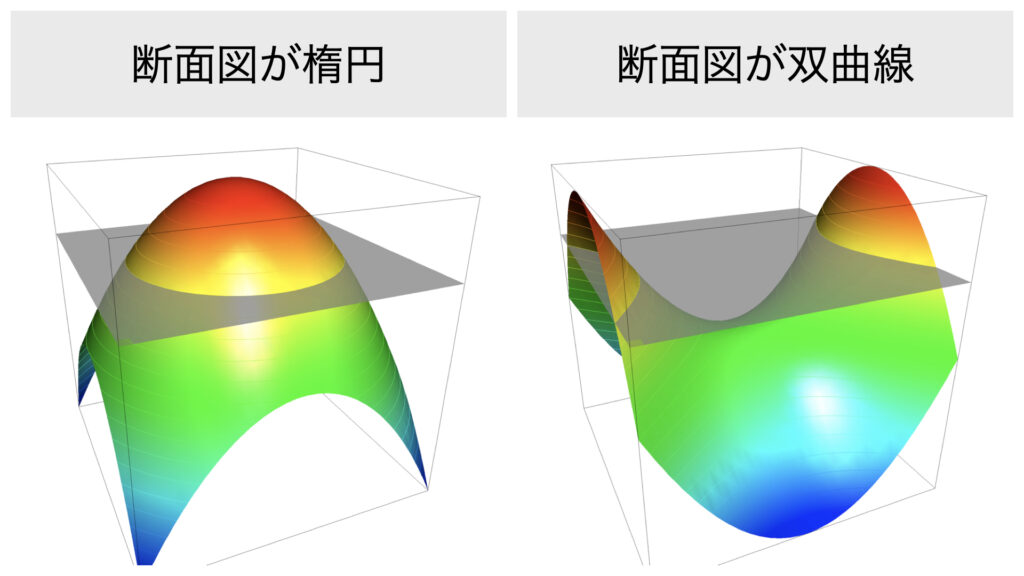
図のように、停留点が極値だった場合の断面図は楕円、停留点が鞍点だった場合の断面図は双曲線、というふうに判定できます。
断面図の式が計算しやすくなるように$f(x,y)$をテイラー展開で近似します。2次の項までテイラー展開すると
$$
f(x,y)
\simeq
f(a,b)
+
f_x(a,b)(x-a) + f_y(a,b)(y-b)
+\displaystyle\frac{1}{2}
\left\{
f_{xx}(a,b)(x-a)^2 + 2f_{xy}(a,b)(x-a)(y-b) + f_{yy}(a,b)(y-b)^2
\right\}
$$
ここで点$(a,b)$が停留点なので以下の条件を満たします。
$$
f_x(a,b)=f_y(a,b)=0
$$
これをテイラー展開の式へ代入して
$$
f(x,y)
\simeq
f(a,b)
+\displaystyle\frac{1}{2}
\left\{
f_{xx}(a,b)(x-a)^2 + 2f_{xy}(a,b)(x-a)(y-b) + f_{yy}(a,b)(y-b)^2
\right\}
$$
となります。ここで式を見やすくするために
$$
\begin{align}
P
&=
f_{xx}(a,b)
\\\\
Q
&=
f_{xy}(a,b)
\\\\
R
&=
f_{yy}(a,b)
\end{align}
$$
とすると
$$
f(x,y)
\simeq
f(a,b)
+\displaystyle\frac{1}{2}
\left\{
P(x-a)^2 + 2Q(x-a)(y-b) + R(y-b)^2
\right\}
\tag{1}
$$
と書けます。この2変数関数の$f(a,b)$付近での断面図を考えます。
切る平面の座標ですが、適当な定数$c$を用いて
$$
z
=
\displaystyle\frac{1}{2}c
+
f(a,b)
$$
で切るとします。その断面図の式は
$$
\displaystyle\frac{1}{2}c
+
f(a,b)
=
f(a,b)
+\displaystyle\frac{1}{2}
\left\{
P(x-a)^2 + 2Q(x-a)(y-b) + R(y-b)^2
\right\}
$$
と書けます。両辺を整理して
$$
c
=
P(x-a)^2 + 2Q(x-a)(y-b) + R(y-b)^2
$$
これが断面図の式です。この関数が楕円か双曲線化を判定すればゴールです。
断面図の式がどんな図形か見分けるために、主軸変換を行って式を見やすくします。
主軸変換は図形を見やすくなるように回転させる計算です。計算式の意味が知りたい方は主軸変換のページをご覧ください。
断面図の式を対称行列を用いて書くと
$$
c
=
\begin{pmatrix}
x-a & y-b
\end{pmatrix}
\begin{pmatrix}
P & Q \\
Q & R
\end{pmatrix}
\begin{pmatrix}
x-a\\
y-b
\end{pmatrix}
\tag{2}
$$
となります。ここで対称行列の対角化計算を行い
$$
\begin{array}{cc}
U
=
\begin{pmatrix}
\lambda_1 & 0 \\
0 & \lambda_2
\end{pmatrix}
&
U
=
\begin{pmatrix}
u_1 & u_2 \\
u_3 & u_4
\end{pmatrix}
\end{array}
$$
このように表される対角行列$D$と直交行列$U$を用いて
$$
{}^tU
\begin{pmatrix}
P & Q \\
Q & R
\end{pmatrix}
U
=
D
$$
が成り立つとします。
次に変換前の$x,y$軸と変換後の$x’,y’$軸の関係を
$$
\begin{pmatrix}
x-a\\
y-b
\end{pmatrix}
=
U
\begin{pmatrix}
x’\\
y’
\end{pmatrix}
$$
とすると、式(2)は
$$
\begin{align}
c
&=
\begin{pmatrix}
x-a & y-b
\end{pmatrix}
\begin{pmatrix}
P & Q \\
Q & R
\end{pmatrix}
\begin{pmatrix}
x-a\\
y-b
\end{pmatrix}
\\\\&=
\begin{pmatrix}
x’ & y’
\end{pmatrix}
{}^tU
\begin{pmatrix}
P & Q \\
Q & R
\end{pmatrix}
U
\begin{pmatrix}
x’\\
y’
\end{pmatrix}
\\\\&=
\begin{pmatrix}
x’ & y’
\end{pmatrix}
D
\begin{pmatrix}
x’\\
y’
\end{pmatrix}
\\\\&=
\lambda_1x’^2+\lambda_2y’^2
\tag{3}
\end{align}
$$
と変形できます。
式(3)は$\lambda_1\lambda_2$の積が$\lambda_1\lambda_2>0$のとき楕円、$\lambda_1\lambda_2<0$のとき双曲線となります。
以上で楕円と双曲線の判定ができたので、$\lambda_1$と$\lambda_2$がどのような値か計算して楕円か双曲線かの条件を求めます。
$\lambda_1,\lambda_2$は対角化計算を行ったあとの対角行列$D$の成分の値でしたので
$$
\begin{align}
\begin{vmatrix}
P-\lambda & Q \\
Q & R-\lambda
\end{vmatrix}
&=
(P-\lambda)(R-\lambda)-Q^2
\\\\&=
\lambda ^2-(P+R)\lambda+PR-Q^2
\end{align}
$$
この式を満たす$\lambda$が$\lambda_1$と$\lambda_2$です。解と係数の関係より
$$
\begin{align}
\lambda_1\lambda_2
&=
PR-Q^2
\\\\&=
\begin{vmatrix}
P & Q \\
Q & R
\end{vmatrix}
\\\\&=
\begin{vmatrix}
f_{xx}(a,b) & f_{xy}(a,b) \\
f_{xy}(a,b) & f_{yy}(a,b)
\end{vmatrix}
\\\\&=
\det H
\end{align}
$$
以上より
$$
\det H = \lambda_1\lambda_2 >0
$$
のとき断面図は楕円になるので$f(a,b)$は極値になります。
$$
\det H = \lambda_1\lambda_2 <0
$$
のとき断面図は双曲線になるので$f(a,b)$は鞍点になります。
次に極大極小の判定について考えます。
式(1)を$y=b$の平面で切ったときの断面図の式は
$$
f(x,b)
\simeq
f(a,b)
+\displaystyle\frac{1}{2}
\left\{
P(x-a)^2
\right\}
$$
これは$x$の1変数関数なので、普段どおりの極大極小の判定と同じことができます。
2階導関数を計算して
$$
\begin{align}
f(x,b)
&\simeq
f(a,b)
+\displaystyle\frac{1}{2}
\left\{
P(x-a)^2
\right\}
\\\\
f'(x,b)
&\simeq
P(x-a)
\\\\
f'{}'(x,b)
&\simeq
P
\end{align}
$$
これより$P>0$なら断面図は下に凸なので$f(a,b)$は極小値となり、$P<0$なら断面図は上に凸なので$f(a,b)$は極大値となります。
$$
P
=
f_{xx}(a,b)
$$
でしたので、$f_{xx}(a,b)>0$なら断面図は下に凸なので$f(a,b)$は極小値となり、$f_{xx}(a,b)<0$なら断面図は上に凸なので$f(a,b)$は極大値となります。
式(1)を$y=b$の平面で切ったときの断面図を計算して条件を出しました。
式(1)を$x=a$の平面で切ったときの断面図を計算して条件を出すと、$f_{yy}(a,b)$の符号によって極大極小の条件が求まります。
$f_{yy}(a,b)>0$なら$f(a,b)$は極小値となり、$f_{yy}(a,b)<0$なら$f(a,b)$は極大値となります。
ヘッセシアンでは判定不能の場合の判定方法
前述の通り$\det H =0$のときはヘッセシアンでは極値か鞍点か判定不能です。
$\det H =0$となる具体例を使って、個別に調べる方法を勉強します。
以下の2変数関数$f(x,y)$を計算します。
$$
f(x,y)
=
x^4-x^2-2xy+y^4-y^2
$$
普段どおりヘッセシアンを求めて、$\det H \neq 0$となる停留点はヘッセシアンで判定しましょう。$\det H =0$となる停留点だけ個別に調べます。
計算3ステップを再掲します。$\det H =0$の場合はステップ4に「判定不能の点を調べる」が追加しましょう。
- 停留点を求める
- ヘッセシアンを求める
- 極値か鞍点か判定する
- 判定不能の点を調べる
ステップ1. 停留点を求める
1階偏導関数を計算して
$$
\begin{align}
f_x(x,y)
&=
4x^3-2x-2y
\\\\
f_y(x,y)
&=
-2x+4y^3-2y
\end{align}
$$
となります。
$$
f_x(x,y)
=
4x^3-2x-2y
=
0
$$
これより$y=2x^3-x$です。これを$f_y(x,y)=0$に代入して
$$
\begin{align}
0
&=
f_y(x,y)
\\\\&=
-2x+4y^3-2y
\\\\&=
-2x+4(2x^3-x)^3-2(2x^3-x)
\\\\&=
8x^9-12x^7+6x^5-2x^3
\\\\&=
2x^3(x-1)(x+1)(4x^4-2x^2+1)
\end{align}
$$
ここで最後の項を平方完成すると
$$
4x^4-2x^2+1
=
4\left\{
\left(
x^2-\displaystyle\frac{1}{4}
\right)^2
+
\displaystyle\frac{15}{16}
\right\}
>0
$$
となるので、$4x^4-2x^2+1=0$を満たす$x$は存在しません。つまり
$$
2x^3(x-1)(x+1)(4x^4-2x^2+1)
=
0
$$
を満たす$x$は$x=-1,0,1$となります。
$y=2x^3-x$の条件と合わせて、停留点は$(x,y)=(-1,-1),$$(0,0),$$(1,1)$の3点です。
ステップ2. ヘッセシアンを求める
2階偏導関数を計算して
$$
\begin{align}
f_{xx}(x,y)
&=
12x^2-2
\\\\
f_{xy}(x,y)
&=
-2
\\\\
f_{yx}(x,y)
&=
-2
\\\\
f_{yy}(x,y)
&=
12y^2-2
\end{align}
$$
となります。ヘッセシアンは
$$
\begin{align}
\det H
&=
\begin{vmatrix}
f_{xx}(x,y) & f_{xy}(x,y) \\
f_{yx}(x,y) & f_{yy}(x,y)
\end{vmatrix}
\\\\&=
\begin{vmatrix}
12x^2-2 & -2 \\
-2 & 12y^2-2
\end{vmatrix}
\\\\&=
24(6x^2y^2-x^2-y^2)
\end{align}
$$
となります。
ステップ3. 極値か鞍点か判定する
停留点$(x,y)=(-1,-1),$$(0,0),$$(1,1)$の3点それぞれで判定します。
$(x,y)=(-1,-1)$のとき、ヘッセシアンは
$$
\begin{align}
\det H
&=
24(6x^2y^2-x^2-y^2)
\\\\&=
96
\end{align}
$$
$\det H >0$なので極値となります。$f_{xx}(-1,-1)=10>0$なので極小値です。
$(x,y)=(0,0)$のとき、ヘッセシアンは
$$
\begin{align}
\det H
&=
24(6x^2y^2-x^2-y^2)
\\\\&=
0
\end{align}
$$
$\det H =0$なので判定不能となります。ステップ4で調べましょう。
$(x,y)=(1,1)$のとき、ヘッセシアンは
$$
\begin{align}
\det H
&=
24(6x^2y^2-x^2-y^2)
\\\\&=
96
\end{align}
$$
$\det H >0$なので極値となります。$f_{xx}(-1,-1)=10>0$なので極小値です。
ステップ4. 判定不能の点を調べる
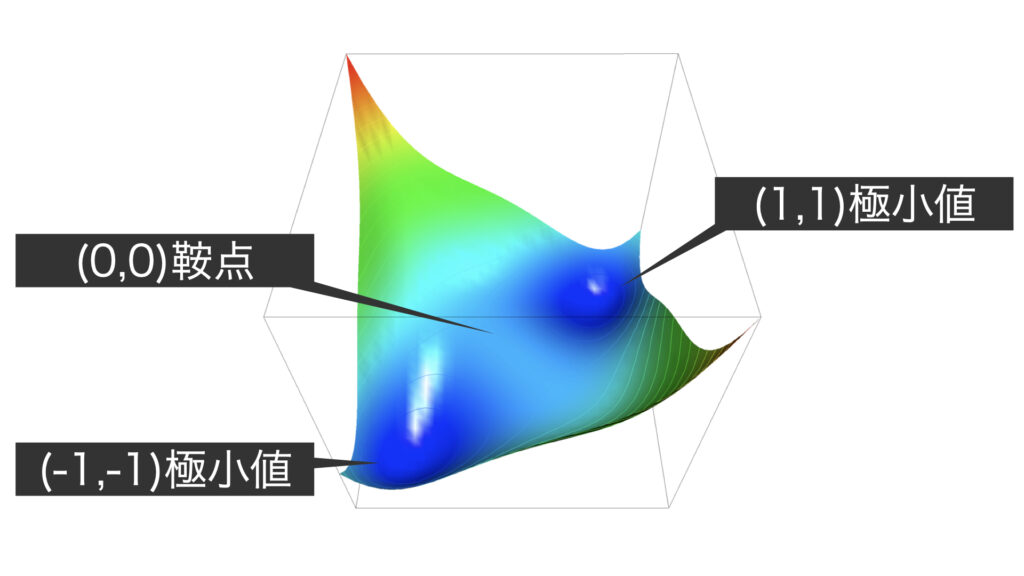
$(x,y)=(0,0)$のときが判定不能なので、個別に調査していきます。
鞍点はある方向から見ると極大値っぽく見えるが別の方向から見ると極小値っぽく見える点のことでした。
$(x,y)=(0,0)$が極大値っぽく見える方向と極小値っぽく見える方向がないか探してみて、見つかれば$(x,y)=(0,0)$は鞍点だと言えます。
それでは計算しましょう。
$f(x,y)$を$x=y$の平面で切った断面図の式は
$$
f(x,x)
=
2x^4-4x^2
$$
となります。これは$x$の1変数関数なので、2階導関数を利用してグラフを書きます。
$$
\begin{align}
f(x,x)
&=
2x^4-4x^2
\\\\
f'(x,x)
&=
8x^3-8x
\\\\&=
8x(x-1)(x+1)
\\\\
f'{}'(x,x)
&=
24x^2-8
\\\\&=
8(3x^2-1)
\end{align}
$$

グラフより$x=0$の点は極大値です。
つまり$f(x,y)$を$x=y$の平面で切ったとき、$f(0,0)$は極大値っぽく見えることが分かりました。
次に$f(x,y)$を$x=-y$の平面で切った断面図の式は
$$
f(x,-x)
=
2x^4
$$
となります。これは$x$の1変数関数なので、2階導関数を利用してグラフを書きます。
$$
\begin{align}
f(x,-x)
&=
2x^4
\\\\
f'(x,-x)
&=
8x^3
\\\\
f'{}'(x,-x)
&=
24x^2
\end{align}
$$

グラフより$x=0$の点は極小値です。
つまり$f(x,y)$を$x=-y$の平面で切ったとき、$f(0,0)$は極小値っぽく見えることが分かりました。
以上の結果より$f(0,0)$は極大値っぽく見える方向と極小値っぽく見える方向があるため鞍点だと判定できます。
なお、$f(x,y)=x^4-x^2-2xy+y^4-y^2$は以下のような曲面です。
まとめ
2変数関数の極値と鞍点の判定はヘッセシアン$\det H$の値で判定できます。
- $\det H >0$なら極値
- $f_{xx}(a,b)>0$もしくは$f_{yy}(a,b)>0$なら極小値
- $f_{xx}(a,b)<0$もしくは$f_{yy}(a,b)<0$なら極大値
- $\det H <0$なら鞍点
- $\det H =0$のときは判定不能
計算方法は以下の3ステップです。
- 停留点を求める
- ヘッセシアンを求める
- 極値か鞍点か判定する





コメント欄