こんにちはコーヤです。
このページでは、逆三角関数の性質を勉強します。様々な分野で登場するので計算に慣れておきましょう。
逆三角関数の定義
その名の通り三角関数の逆関数のことです。”arc”をつけて表現します。
$$
\begin{align}
y&=\sin x
\\\\
x&=\arcsin y
\end{align}
$$
三角関数の式を逆関数にしただけです。
それでは3種類の逆三角関数について、グラフや微積を見ていきます。
arcsinの性質
グラフ
$y=\arcsin x$のグラフは以下のような概形です。
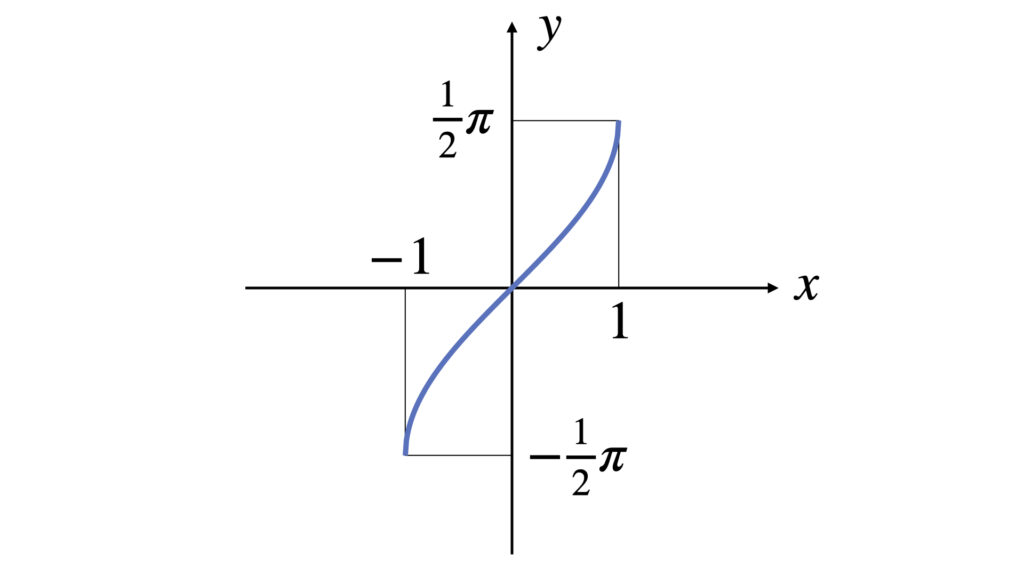
定義域は$-1 \leq x \leq 1$です。
値域は$-\displaystyle\frac{1}{2}\pi \leq y \leq \displaystyle\frac{1}{2}\pi$です。
微分
$y=\arcsin x$を微分すると以下のようになります。
$$
y’=\frac{1}{\sqrt{1-x^2}}
$$
微分の導出過程です。
$$
\begin{array}{cc}
x=\sin y
&
\left(
-\displaystyle\frac{1}{2}\pi \leq y \leq \displaystyle\frac{1}{2}\pi
\right)
\end{array}
$$
両辺$y$で微分して
$$
\begin{array}{cc}
\displaystyle\frac{dx}{dy}=\cos y
&
(0 \leq \cos y \leq 1)
\end{array}
$$
分母分子を入れ替えて
$$
\begin{align}
\displaystyle\frac{dy}{dx}
&=
\displaystyle\frac{1}{\cos y}
\\\\&=
\displaystyle\frac{1}{\sqrt{1-\sin ^2 y}}
\\\\&=
\displaystyle\frac{1}{\sqrt{1-x^2}}
\end{align}
$$
となります。
積分
$\arcsin x$を積分すると以下のようになります。
$$
\displaystyle \int \arcsin x ~dx
=
x\arcsin x+\sqrt{1-x^2}+C
$$
積分の導出過程です。部分積分を使って
$$
\begin{align}
\displaystyle \int \arcsin x ~dx
&=
x\arcsin x-\displaystyle\int \displaystyle\frac{x}{\sqrt{1-x^2}} ~dx
\\\\&=
x\arcsin x+\sqrt{1-x^2}+C
\end{align}
$$
となります。
arccosの性質
グラフ
$y=\arccos x$のグラフは以下のような概形です。
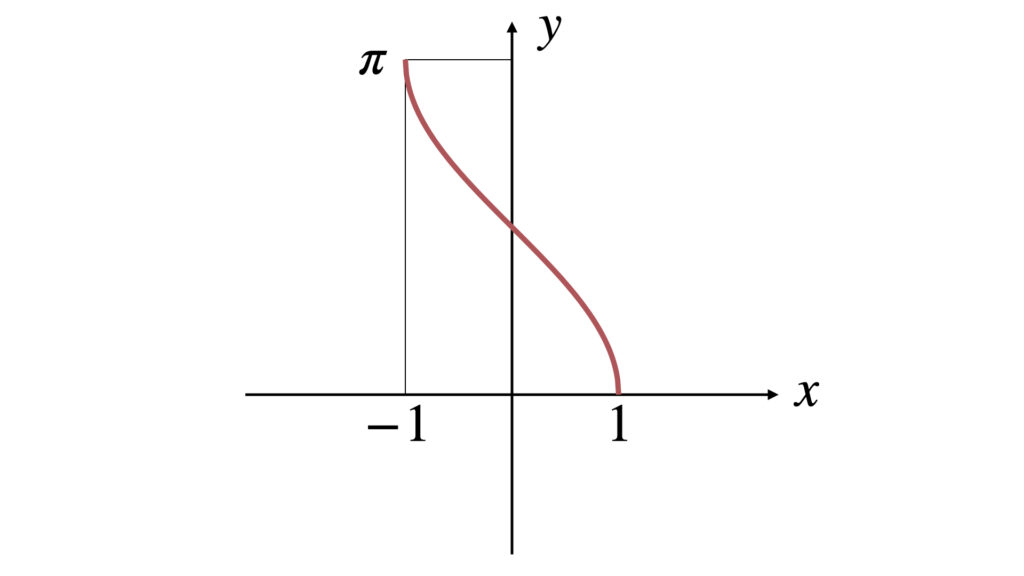
定義域は$-1 \leq x \leq 1$です。
値域は$0 \leq y \leq \pi$です。
微分
$y=\arccos x$を微分すると以下のようになります。
$$
y’=-\displaystyle\frac{1}{\sqrt{1-x^2}}
$$
微分の導出過程です。
$$
\begin{array}{cc}
x=\cos y
&
\left(
0 \leq y \leq \pi
\right)
\end{array}
$$
両辺$y$で微分して
$$
\begin{array}{cc}
\displaystyle\frac{dx}{dy}=-\sin y
&
(0 \leq \sin y \leq 1)
\end{array}
$$
分母分子を入れ替えて
$$
\begin{align}
\displaystyle\frac{dy}{dx}
&=
-\displaystyle\frac{1}{\sin y}
\\\\&=
-\displaystyle\frac{1}{\sqrt{1-\cos ^2 y}}
\\\\&=
-\displaystyle\frac{1}{\sqrt{1-x^2}}
\end{align}
$$
となります。
積分
$\arccos x$を積分すると以下のようになります。
$$
\displaystyle \int \arccos x ~dx
=
x\arccos x-\sqrt{1-x^2}+C
$$
積分の導出過程です。部分積分を使って
$$
\begin{align}
\displaystyle \int \arccos x ~dx
&=
x\arccos x+\displaystyle\int \displaystyle\frac{x}{\sqrt{1-x^2}} ~dx
\\\\&=
x\arccos x-\sqrt{1-x^2}+C
\end{align}
$$
となります。
arctanの性質
グラフ
$y=\arctan x$のグラフは以下のような概形です。
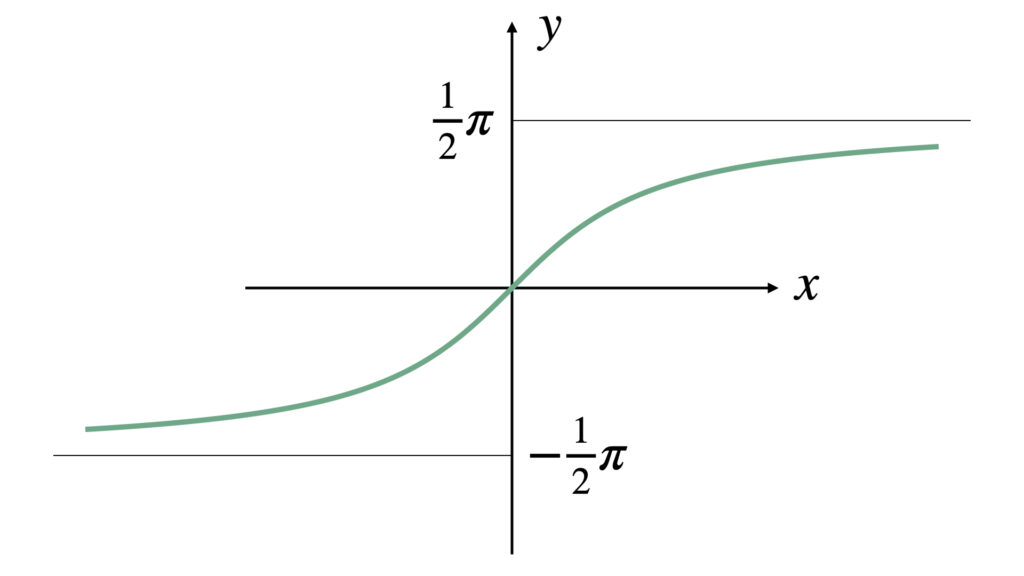
定義域は$-\infty < x < \infty$です。
値域は$-\displaystyle\frac{1}{2}\pi < y < \displaystyle\frac{1}{2}\pi$です。
微分
$y=\arctan x$を微分すると以下のようになります。
$$
y’=\displaystyle\frac{1}{1+x^2}
$$
微分の導出過程です。
$$
\begin{array}{cc}
x=\tan y
&
\left(
-\displaystyle\frac{1}{2}\pi < y < \displaystyle\frac{1}{2}\pi
\right)
\end{array}
$$
両辺$y$で微分して
$$
\displaystyle\frac{dx}{dy}=\displaystyle\frac{1}{\cos^2 y}
$$
分母分子を入れ替えて
$$
\begin{align}
\displaystyle\frac{dy}{dx}
&=
\cos^2 y
\\\\&=
\displaystyle\frac{1}{1+\tan^2 y}
\\\\&=
\displaystyle\frac{1}{1+x^2}
\end{align}
$$
となります。
積分
$\arctan x$を積分すると以下のようになります。
$$
\displaystyle \int \arctan x ~dx
=
x\arctan x
-\displaystyle\frac{1}{2}\log(1+x^2)+C
$$
積分の導出過程です。部分積分を使って
$$
\begin{align}
\displaystyle \int \arctan x ~dx
&=
x\arctan x-\displaystyle\int \displaystyle\frac{x}{1+x^2} ~dx
\\\\&=
x\arctan x
-\displaystyle\frac{1}{2}\log(1+x^2)+C
\end{align}
$$
となります。
三角関数の合成
三角関数の合成の公式は$\arctan$を使って表現することができます。
合成公式
$$
a\sin x + b\cos x
=
\sqrt{a^2+b^2}
\sin
\left(
x+\arctan\displaystyle\frac{b}{a}
\right)
$$
$$
a\sin x + b\cos x
=
\sqrt{a^2+b^2}
\cos
\left(
x-\arctan\displaystyle\frac{a}{b}
\right)
$$
導出
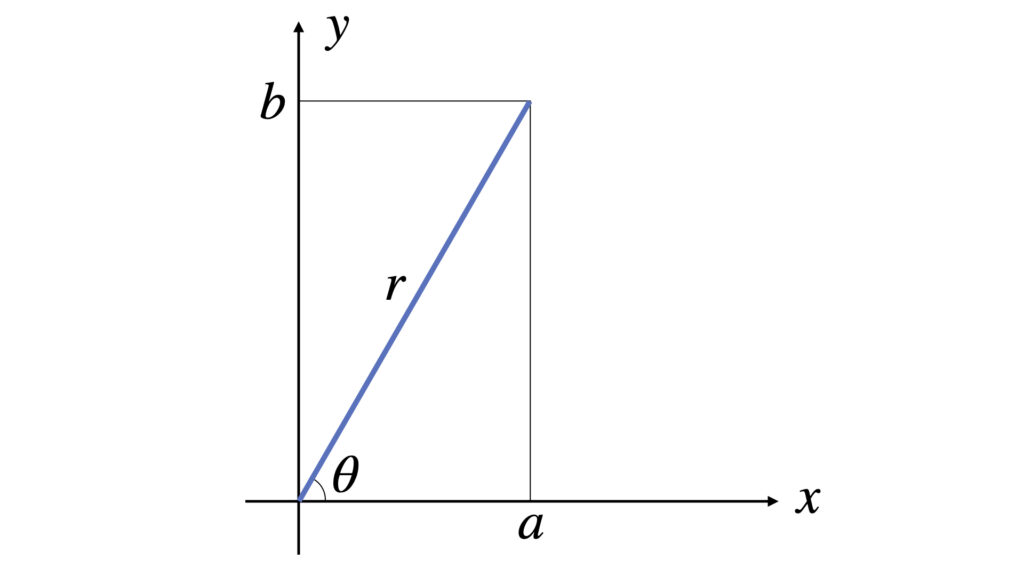
図のような適当な点$(a,b)$を極座標で表します。
$$
\begin{align}
a &= r \cos \theta
\\\\
b &= r \sin \theta
\\\\
r &= \sqrt{a^2+b^2}
\end{align}
$$
$$
\begin{align}
\tan \theta &= \frac{r \sin \theta}{r \cos \theta} = \frac{b}{a}
\\\\
\theta &= \arctan \displaystyle\frac{b}{a}
\end{align}
$$
これらの式を使って導出します。まずは$\sin$の合成公式の導出です。
$$
\begin{align}
a \sin x + b \cos x
&=
r \cos \theta \sin x + r \sin \theta \cos x
\\\\&=
r \left( \sin x \cos \theta + \cos x \sin \theta \right)
\\\\&=
r \sin \left( x + \theta \right)
\\\\&=
\sqrt{a^2+b^2} \sin \left( x + \arctan \displaystyle\frac{b}{a} \right)
\end{align}
$$
次に$\cos$の合成公式の導出です。
$$
\begin{align}
a \cos x + b \sin x
&=
r \cos \theta \cos x + r \sin \theta \sin x
\\\\&=
r \left( \cos x \cos \theta + \sin x \sin \theta \right)
\\\\&=
r \cos \left( x-\theta \right)
\\\\&=
\sqrt{a^2+b^2} \cos \left( x-\arctan \displaystyle\frac{b}{a} \right)
\end{align}
$$
ここで$a$と$b$を入れ替えると公式が導出できます。
$$
a\sin x + b\cos x
=
\sqrt{a^2+b^2}
\cos
\left(
x-\arctan\displaystyle\frac{a}{b}
\right)
$$
逆三角関数の例題
それでは例題6つで逆三角関数の計算に慣れましょう。逆三角関数で表された値を求める問題と逆三角関数で置換する積分の問題です。
例題1
$$
\sin
\left(
\arccos
\displaystyle\frac{1}{2}
\right)
$$
まず$\arccos$の値を求めます。
$$
\arccos
\displaystyle\frac{1}{2}
=
\displaystyle\frac{1}{3}\pi
$$
これを代入します。
$$
\sin
\displaystyle\frac{1}{3}\pi
=
\displaystyle\frac{\sqrt{3}}{2}
$$
例題2
$$
\sin
\left(
\arccos x
\right)
$$
例題1を一般化した問題です。
逆三角関数が変数になっていたら、文字でおいて普通の三角関数に戻すところから始めます。
変数の範囲の確認を忘れないように注意しましょう。
$$
\begin{array}{cc}
\arccos x=p
&
\left(
0 \leq p \leq \pi
\right)
\end{array}
$$
文字でおいたら普通の三角関数に戻します。
$$
\cos p=x
$$
$0 \leq p \leq \pi$より$\sin p \geq 0$となるので
$$
\begin{align}
\sin p
&=
\sqrt{1-\cos^2 p}
\\\\&=
\sqrt{1-x^2}
\end{align}
$$
以上より
$$
\sin
\left(
\arccos x
\right)
=
\sqrt{1-x^2}
$$
です。
例題3
$$
\arctan 2 + \arctan 3
$$
$\arctan 2$や$\arctan 3$は具体的な数値がわかりません。こういうときも文字でおいて普通の三角関数に戻すところから始めます。
$$
\begin{array}{cc}
\arctan 2=p
&
\left(
-\displaystyle\frac{1}{2}\pi < p < \displaystyle\frac{1}{2}\pi
\right)
\end{array}
$$
文字でおいたら普通の三角関数に戻します。
$$
\begin{array}{cc}
\tan p=2
&
\left(
0 < p < \displaystyle\frac{1}{2}\pi
\right)
\end{array}
$$
$\tan p$の値が正のため、$p > 0$の範囲であることが分かりました。
同様に$\arctan 3$も文字でおきます。
$$
\begin{array}{cc}
\arctan 3=q
&
\left(
-\displaystyle\frac{1}{2}\pi < q < \displaystyle\frac{1}{2}\pi
\right)
\end{array}
$$
$$
\begin{array}{cc}
\tan q=3
&
\left(
0 < q < \displaystyle\frac{1}{2}\pi
\right)
\end{array}
$$
これらの結果を用いて加法定理を使います。
$$
\begin{align}
\tan(p+q)
&=
\displaystyle\frac{\tan p + \tan q}{1-\tan p\tan q}
\\\\&=
\displaystyle\frac{2 + 3}{1-6}
\\\\&=
-1
\end{align}
$$
これを満たす$p+q$は整数$n$を用いて
$$
p+q
=
-\displaystyle\frac{1}{4}\pi
+n\pi
$$
と表されます。
ここで$p,q$の範囲より
$$
0 < p+q < \pi
$$
となるので
$$
p+q
=
\displaystyle\frac{3}{4}\pi
$$
です。これより
$$
\begin{align}
\arctan 2 + \arctan 3
&=
p+q
\\\\&=
\displaystyle\frac{3}{4}\pi
\end{align}
$$
となります。
例題4
$$
\arcsin x + \arccos x
$$
文字でおくところから始めます。
$$
\begin{array}{cc}
\arcsin x=p
&
\left(
-\displaystyle\frac{1}{2}\pi \leq p \leq \displaystyle\frac{1}{2}\pi
\right)
\end{array}
$$
文字でおいたら普通の三角関数に戻します。
$$
\sin p=x
$$
同様に
$$
\begin{array}{cc}
\arccos x=q
&
\left(
0 \leq q \leq \pi
\right)
\end{array}
$$
$$
\cos q=x
$$
以上より
$$
\sin p = \cos q
$$
です。ここで$\cos q$を$\sin$に変換します。
$$
\begin{array}{cc}
\cos q
=
\sin
\left(
\displaystyle\frac{1}{2}\pi-q
\right)
&
\left(
-\displaystyle\frac{1}{2}\pi \leq \displaystyle\frac{1}{2}\pi-q \leq \displaystyle\frac{1}{2}\pi
\right)
\end{array}
$$
変換には以下の公式を使いました。
$$
\cos \theta
=
\sin
\left(
\displaystyle\frac{1}{2}\pi
-\theta
\right)
$$
以上より
$$
\sin p
=
\sin
\left(
\displaystyle\frac{1}{2}\pi-q
\right)
$$
となるので
$$
p=\displaystyle\frac{1}{2}\pi-q
$$
です。これを用いて与式は
$$
\begin{align}
\arcsin x + \arccos x
&=
p+q
\\\\&=
\displaystyle\frac{1}{2}\pi
\end{align}
$$
となります。
例題5
$$
\displaystyle\int
\displaystyle\frac{1}{\sqrt{1-x^2}}
~dx
$$
$x=\sin t$と置換します。
$$
\begin{array}{cc}
x=\sin t
&
\left(
-\displaystyle\frac{1}{2}\pi
\leq
t
\leq
\displaystyle\frac{1}{2}\pi
\right)
\end{array}
$$
これより
$$
\begin{array}{cc}
t=\arcsin x
&
\left(
-1
\leq
x
\leq
1
\right)
\end{array}
$$
両辺$x$で微分して
$$
\displaystyle\frac{dt}{dx}
=
\displaystyle\frac{1}{\sqrt{1-x^2}}
$$
これを積分に代入して
$$
\begin{align}
\displaystyle\int
\displaystyle\frac{1}{\sqrt{1-x^2}}
~dx
&=
\displaystyle\int
~dt
\\\\&=
t+C
\\\\&=
\arcsin x +C
\end{align}
$$
となります。
例題6
$$
\displaystyle\int
\displaystyle\frac{1}{1+x^2}
~dx
$$
$x=\tan t$と置換します。
$$
\begin{array}{cc}
x=\tan t
&
\left(
-\displaystyle\frac{1}{2}\pi
<
t
<
\displaystyle\frac{1}{2}\pi
\right)
\end{array}
$$
これより
$$
\begin{array}{cc}
t=\arctan x
&
\left(
-\infty
\leq
x
\leq
\infty
\right)
\end{array}
$$
両辺$x$で微分して
$$
\displaystyle\frac{dt}{dx}
=
\displaystyle\frac{1}{1+x^2}
$$
これを積分に代入して
$$
\begin{align}
\displaystyle\int
\displaystyle\frac{1}{1+x^2}
~dx
&=
\displaystyle\int
~dt
\\\\&=
t+C
\\\\&=
\arctan x +C
\end{align}
$$
となります。
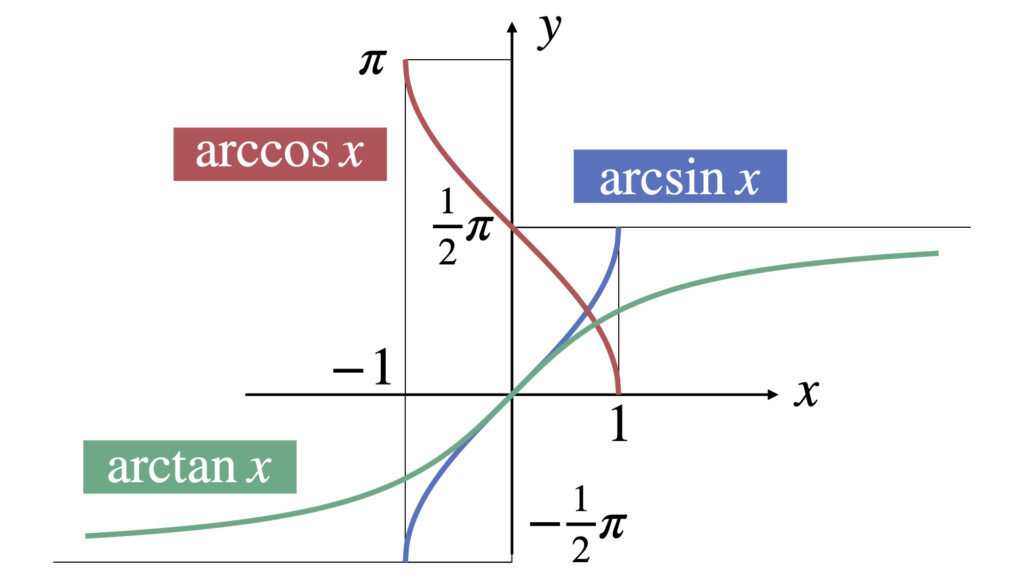
まとめ
逆三角関数のグラフは以下のとおりです。



コメント欄