こんにちはコーヤです。
このページでは、数列を無限項まで足したときの和の無限級数の計算方法を勉強します。
無限級数の計算方法
数列$a_n$の無限級数$S$の計算方法は2ステップです。
- $n$項目までの和$S_n$を求める
- $S_n$を$n\to\infty$にする
式で2ステップを見ていきます。数列$a_n$の$n$項目までの和$S_n$は以下のように表されます。
$$
S_n
=
\displaystyle\sum_{k=1}^n
a_k
$$
このとき無限級数$S$は
$$
S
=
\displaystyle\lim_{n \to \infty}
S_n
$$
となります。
ステップ1で$n$項目までの和$S_n$を求め、ステップ2で$n\to\infty$にします。
2ステップに分けるのをめんどくさがって、いきなり無限項の和を求めると失敗してしまうので要注意です。
フィボナッチ数列を使って失敗例と成功例の違いを見てみましょう。
フィボナッチ数列の無限級数
フィボナッチ数列$F_n$は第1項が1、第2項も1、第3項以降は前の2個を足したものです。数式で表すと以下のようになります。
$$
\begin{align}
F_1&=1\\\\
F_2&=1\\\\
F_n&=F_{n-1}+F_{n-2}
\end{align}
$$
実際にフィボナッチ数列を書き出して見みます。
$$
\begin{array}{ccccccccccc}
1,&1,&2,&3,&5,&8,&13,&21,&34&\cdots
\end{array}
$$
それではフィボナッチ数列の無限級数を求めてみましょう。失敗例と成功例の2パターンです。
失敗例
無限級数$S$の式は以下のようになります。
$$
S=1+1+2+3+5+8+13+21+34\cdots
$$
$S$を1段ずらして書いてみます。
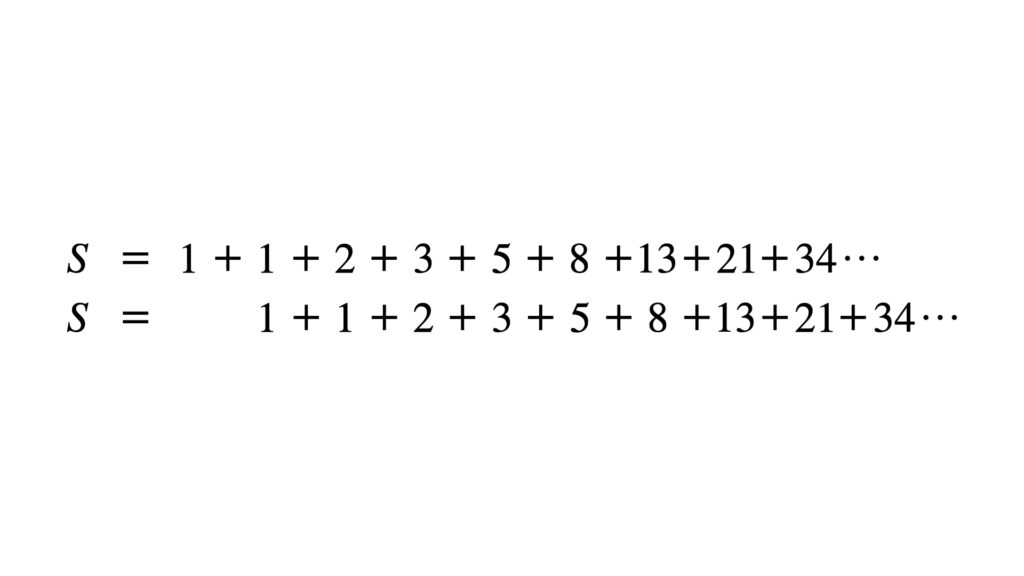
この2式を足し合わせて$2S$にします。青の矢印のように縦に足し合わせます。
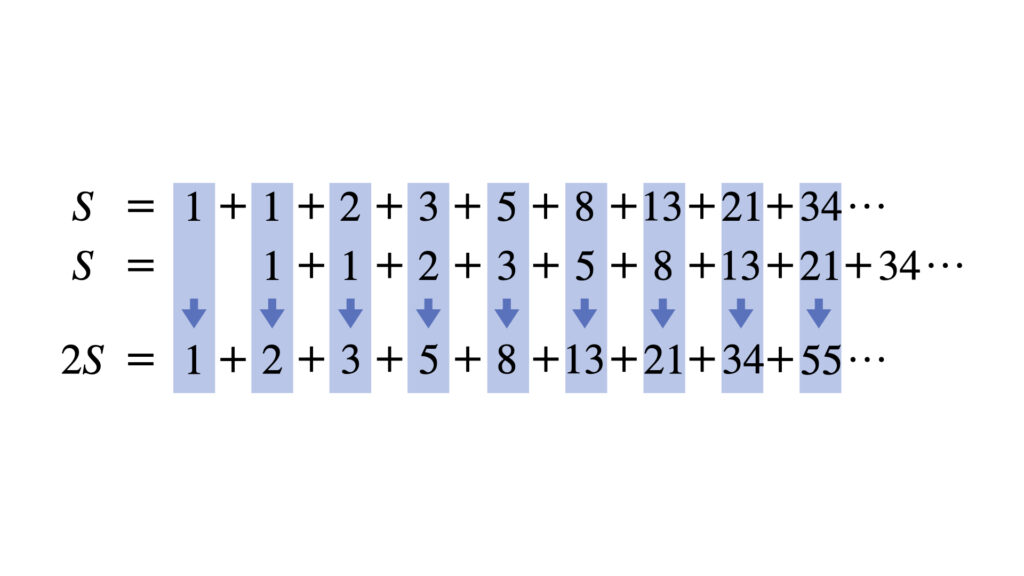
$S$の式と$2S$の式を見比べると、赤で示した部分が一致しています。
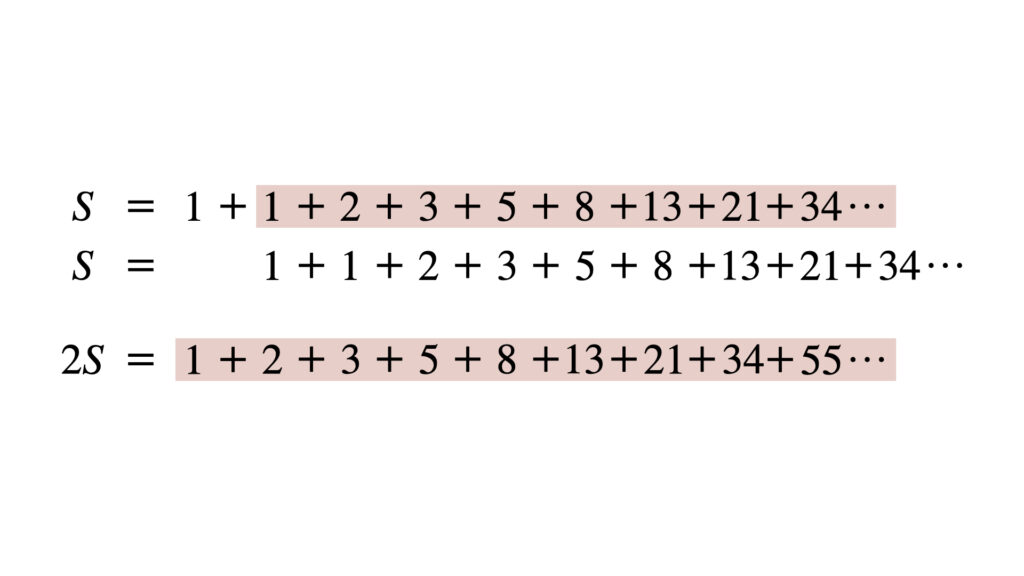
この赤の部分の値を$\alpha$としましょう。
2式を$\alpha$を使って表すと
$$
\begin{align}
S&=1+\alpha
\\\\
2S&=\alpha
\end{align}
$$
2式から$\alpha$を消して
$$
2S=S-1
$$
これよりフィボナッチ数列の無限級数$S$は
$$
S=-1
$$
となってしまいます。つまり
$$
-1=1+1+2+3+5+8+13+21+34\cdots
$$
こうなります。明らかに間違った結果になってしまいました。
こんな失敗をしてしまった原因は、$n$項目までの総和$S_n$を求めずにいきなり無限項の和を求めたからです。
成功例
まずは$n$項目までの和$S_n$を求めてみます。$S_n$は以下のように表されます。
$$
S_n
=
\displaystyle\sum_{k=1}^{n}
F_k
$$
フィボナッチ数列の$n$項目は以下のように定義されていました。
$$
F_n=F_{n-1}+F_{n-2}
$$
これを移項して
$$
F_{n-2}=F_n-F_{n-1}
$$
この式に従って1項目から順に書き出して行きます。
$$
\begin{align}
F_1&=F_3-F_2\\\\
F_2&=F_4-F_3\\\\
F_3&=F_5-F_4\\\\
F_4&=F_6-F_5\\\\
\vdots\\\\
F_n&=F_{n+2}-F_{n-1}
\end{align}
$$
これらの左辺を足し合わせたものが$S_n$になります。右辺は足し合わせると符号で打ち消し合います。
$$
\begin{align}
F_1&=\cancel{F_3}-F_2
\\\\
F_2&=\cancel{F_4}-\cancel{F_3}
\\\\
F_3&=\cancel{F_5}-\cancel{F_4}
\\\\
F_4&=\cancel{F_6}-\cancel{F_5}
\\\\
\vdots
\\\\
F_n&=F_{n+2}-\cancel{F_{n-1}}
\end{align}
$$
両辺足し合わせた結果は以下のようになります。
$$
S_n
=
F_{n+2}-F_2
$$
第2項目は$F_2=1$なので
$$
S_n
=
F_{n+2}-1
$$
です。ここまででステップ1が終了です。ステップ2の$n\to\infty$をしましょう。
$$
\begin{align}
S
&=
\displaystyle\lim_{n \to \infty}
S_n
\\\\&=
\displaystyle\lim_{n \to \infty}
\left(
F_{n+2}
-1
\right)
\\\\&=
\infty
\end{align}
$$
正の無限大に発散するというイメージ通りの結果が得られました。
無限級数の例題
それでは例題5つで無限級数を計算してみましょう。
階差の形に式変形するか、等比数列の和を利用するパターンがほとんどです。
例題1
$$
\displaystyle\sum_{n=1}^\infty
\displaystyle\frac{1}{n(n+1)}
$$
部分分数分解で階差の形に式変形します。
$$
\begin{align}
S_n
&=
\displaystyle\sum_{k=1}^n
\displaystyle\frac{1}{k(k+1)}
\\\\&=
\displaystyle\sum_{k=1}^n
\left(
\displaystyle\frac{1}{k}-\displaystyle\frac{1}{k+1}
\right)
\end{align}
$$
これを展開して
$$
\begin{align}
\displaystyle\sum_{k=1}^n
\left(
\displaystyle\frac{1}{k}-\displaystyle\frac{1}{k+1}
\right)
&=
\left(
1-\displaystyle\frac{1}{2}
\right)
+
\left(
\displaystyle\frac{1}{2}-\displaystyle\frac{1}{3}
\right)
+
\cdots
+
\left(
\displaystyle\frac{1}{n}-\displaystyle\frac{1}{n+1}
\right)
\\\\&=
1-\displaystyle\frac{1}{n+1}
\end{align}
$$
ここから$n\to\infty$にして
$$
\begin{align}
S
&=
\displaystyle\lim_{n \to \infty}
S_n
\\\\&=
\displaystyle\lim_{n \to \infty}
\left(
1-\displaystyle\frac{1}{n+1}
\right)
\\\\&=
1
\end{align}
$$
です。
例題2
$$
\displaystyle\sum_{n=1}^\infty
\log
\left(
1+\displaystyle\frac{1}{n}
\right)
$$
$\log$を2つに分けて階差の形に式変形します。
$$
\begin{align}
S_n
&=
\displaystyle\sum_{k=1}^n
\log
\left(
1+\displaystyle\frac{1}{k}
\right)
\\\\&=
\displaystyle\sum_{k=1}^n
\log
\left(
\displaystyle\frac{k+1}{k}
\right)
\\\\&=
\displaystyle\sum_{k=1}^n
\left\{
\log(k+1)-\log k
\right\}
\end{align}
$$
これを展開して
$$
\begin{align}
\displaystyle\sum_{k=1}^n
\left\{
\log(k+1)-\log k
\right\}
&=
(\log 2 -\log 1)
+
(\log 3 -\log 2)
+
\cdots
+
\{\log(n+1) -\log n\}
\\\\&=
\log(n+1) -\log 1
\\\\&=
\log(n+1)
\end{align}
$$
ここから$n\to\infty$にして
$$
\begin{align}
S
&=
\displaystyle\lim_{n \to \infty}
S_n
\\\\&=
\displaystyle\lim_{n \to \infty}
\log(n+1)
\\\\&=
\infty
\end{align}
$$
です。
例題3
$$
\displaystyle\sum_{n=1}^\infty
\displaystyle\frac{1}{\sqrt{n}+\sqrt{n+1}}
$$
有理化して階差の形に式変形します。
$$
\begin{align}
S_n
&=
\displaystyle\sum_{k=1}^n
\displaystyle\frac{1}{\sqrt{k}+\sqrt{k+1}}
\\\\&=
\displaystyle\sum_{k=1}^n
\left(
\sqrt{k+1}-\sqrt{k}
\right)
\end{align}
$$
これを展開して
$$
\begin{align}
\displaystyle\sum_{k=1}^n
\left(
\sqrt{k+1}-\sqrt{k}
\right)
&=
\left(
\sqrt{2}-1
\right)
+
\left(
\sqrt{3}-\sqrt{2}
\right)
+
\cdots
+\left(
\sqrt{n+1}-\sqrt{n}
\right)
\\\\&=
\sqrt{n+1}-1
\end{align}
$$
ここから$n\to\infty$にして
$$
\begin{align}
S
&=
\displaystyle\lim_{n \to \infty}
S_n
\\\\&=
\displaystyle\lim_{n \to \infty}
\left(
\sqrt{n+1}-1
\right)
\\\\&=
\infty
\end{align}
$$
です。
例題4
$$
\displaystyle\sum_{n=1}^\infty
\displaystyle\frac{\cos (n \pi)}{2^n}
$$
まずは$S_n$の式にして
$$
S_n
=
\displaystyle\sum_{k=1}^n
\displaystyle\frac{\cos (k \pi)}{2^k}
$$
シグマの部分を展開します。
$$
S_n
=
\displaystyle\frac{-1}{2}
+
\displaystyle\frac{1}{4}
+
\displaystyle\frac{-1}{8}
+
\cdots
+
\displaystyle\frac{\cos (n \pi)}{2^n}
\tag{1}
$$
両辺に$\displaystyle\frac{1}{2}$をかけて
$$
\displaystyle\frac{1}{2}
S_n
=
\displaystyle\frac{-1}{4}
+
\displaystyle\frac{1}{8}
+
\displaystyle\frac{-1}{16}
+
\cdots
+
\displaystyle\frac{\cos \{(n-1) \pi\}}{2^n}
+
\displaystyle\frac{\cos (n \pi)}{2^{n+1}}
\tag{2}
$$
式(1)と式(2)を足して
$$
\displaystyle\frac{3}{2}
S_n
=
\displaystyle\frac{-1}{2}
+
\displaystyle\frac{\cos (n \pi)}{2^{n+1}}
$$
左辺の$\displaystyle\frac{3}{2}$を移項して
$$
S_n
=
\displaystyle\frac{-1}{3}
+
\displaystyle\frac{\cos (n \pi)}{3 \cdot 2^n}
$$
ここから$n\to\infty$にして
$$
\begin{align}
S
&=
\displaystyle\lim_{n \to \infty}
S_n
\\\\&=
\displaystyle\lim_{n \to \infty}
\left(
\displaystyle\frac{-1}{3}
+
\displaystyle\frac{\cos (n \pi)}{3 \cdot 2^n}
\right)
\\\\&=
-\displaystyle\frac{1}{3}
\end{align}
$$
です。
例題5
$$
\displaystyle\sum_{n=1}^\infty
2^n\cos (n \pi)
$$
まずは$S_n$の式にして
$$
S_n
=
\displaystyle\sum_{k=1}^n
2^k\cos (k \pi)
$$
シグマの部分を展開します。
$$
S_n
=
-2+4-8-16+32+
\cdots
$$
$S_n$は振動しています。こういう場合は無限級数も振動と扱います。
まとめ
数列$a_n$の無限級数$S$の計算方法は2ステップです。
- $n$項目までの和$S_n$を求める
- $S_n$を$n\to\infty$にする




コメント欄