こんにちはコーヤです。
このページでは、無限級数が収束するかどうかの判定法をダランベール、コーシー、ラーベの3種類勉強します。数列の分野だけでなくテイラー展開の分野でも必須の知識です。
収束判定法の目的
数列$a_n$の$n$項目までの和$S_n$は以下のように表されます。
$$
S_n
=
\displaystyle\sum_{k=1}^n
a_k
$$
このとき無限級数$S$は
$$
S
=
\displaystyle\lim_{n \to \infty}
S_n
$$
となります。
ステップ1で$n$項目までの和$S_n$を求め、ステップ2で$n\to\infty$にします。
では以下の無限級数は求まるでしょうか。
$$
\displaystyle\sum_{n=1}^\infty
\displaystyle\frac{n^n}{n!}
$$
これの$S_n$を手計算するのは至難の業です。
でもステップ1の$S_n$が求められないとステップ2に進めません。どうやって無限級数$S$を求めればいいでしょうか。
・・・こういうときに役立つのが収束判定法です。
収束判定法を使えば無限級数$S$が収束するかどうかを判定することができます。
収束する値を求めることはできませんが、妥協案として収束するかどうかだけは判定しようということです。
収束判定法を使うときの注意
収束判定法を使う前の準備として、数列の全ての項の絶対値を取る作業が必要です。
絶対値を取った数列の無限級数$S=\displaystyle\sum_{n=1}^\infty |a_n|$が収束した場合は、絶対値を取る前の数列の無限級数$S=\displaystyle\sum_{n=1}^\infty a_n$も必ず収束します。
これを絶対収束と言います。

「無限級数$S=\displaystyle\sum_{n=1}^\infty a_n$は絶対収束する」と「無限級数$S=\displaystyle\sum_{n=1}^\infty |a_n|$は収束する」が同じ意味です。
絶対値を取った数列の無限級数が発散した場合、絶対値を取る前の数列の無限級数は正の無限大に発散、負の無限大に発散、振動、のいずれかになります。
正の無限大に発散、負の無限大に発散、振動の3パターンは、全ての項の絶対値を取ると3パターンとも正の無限大に発散となります。
$$
\begin{array}{cllll}
(1)&1+2+3+\cdots+n+\cdots&\to&S=\infty
\\\\
(2)&-1-2-3-\cdots-n-\cdots&\to&S=-\infty
\\\\
(3)&-1+1-1+\cdots+(-1)^n+\cdots&\to&S=\times
\end{array}
$$
それぞれ無限級数$S$は正の無限大に発散、負の無限大に発散、振動です。
これらの数列の絶対値を取ってから無限級数$S$を計算すると以下のようになります。
$$
\begin{array}{cllll}
(1{}’)&|1|+|2|+|3|+\cdots+|n|+\cdots&\to&S=\infty
\\\\
(2{}’)&|-1|+|-2|+|-3|+\cdots+|-n|+\cdots&\to&S=\infty
\\\\
(3{}’)&|-1|+|1|+|-1|+\cdots+\left|(-1)^n\right|+\cdots&\to&S=\infty
\end{array}
$$
このように3パターンとも正の無限大に発散となります。
収束判定法はあくまで「収束」「発散」を判定する方法です。
「収束」と判定されたからといって無限級数の値は分かりませんし、「発散」と判定されたからといって、それが正の無限大に発散、負の無限大に発散、振動、のどれになるかまでは分かりません。

すべての項が0以上の数列の無限級数のことを正項級数と言います。
収束判定法は正項級数にしか使えないので、絶対値を取る作業で正項級数ではないものを正項級数へ変換しています。
ダランベールの収束判定法
$$
r
=
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{a_{n+1}}{a_n}
$$
としたとき正項級数$\displaystyle\sum_{n=1}^\infty a_n$は
- $0 \leq r <1$のとき収束
- $r=1$のとき判定不能
- $1 < r$のとき発散
となります。
それでは例題4つでダランベールの収束判定法の使い方を見ていきましょう。
例題1
$$
\displaystyle\sum_{n=1}^\infty
\displaystyle\frac{1}{n!}
$$
まずは$a_n$から$a_{n+1}$の形を求めます。
$$
\begin{align}
a_n
&=
\displaystyle\frac{1}{n!}
\\\\
a_{n+1}
&=
\displaystyle\frac{1}{(n+1)!}
\end{align}
$$
これより
$$
\begin{align}
r
&=
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{a_{n+1}}{a_n}
\\\\&=
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{n!}{(n+1)!}
\\\\&=
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{1}{n+1}
\\\\&=
0
\end{align}
$$
$0 \leq r <1$のときに当てはまるので収束します。
例題2
$$
\displaystyle\sum_{n=1}^\infty
\displaystyle\frac{n^n}{n!}
$$
まずは$a_n$から$a_{n+1}$の形を求めます。
$$
\begin{align}
a_n
&=
\displaystyle\frac{n^n}{n!}
\\\\
a_{n+1}
&=
\displaystyle\frac{(n+1)^{n+1}}{(n+1)!}
\end{align}
$$
これより
$$
\begin{align}
r
&=
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{a_{n+1}}{a_n}
\\\\&=
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{(n+1)^{n+1}}{n^n}
\cdot
\displaystyle\frac{n!}{(n+1)!}
\\\\&=
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{(n+1)^n \cdot (n+1)}{n^n}
\cdot
\displaystyle\frac{1}{n+1}
\\\\&=
\displaystyle\lim_{n \to \infty}
\left(
\displaystyle\frac{n+1}{n}
\right)
^n
\\\\&=
\displaystyle\lim_{n \to \infty}
\left(
1+ \displaystyle\frac{1}{n}
\right)
^n
\\\\&=
e
\end{align}
$$
$1 < r$のときに当てはまるので発散します。
例題3
$$
\displaystyle\sum_{n=1}^\infty
\left(
n+\displaystyle\frac{1}{n}
\right)
^n
$$
まずは$a_n$から$a_{n+1}$の形を求めます。
$$
\begin{align}
a_n
&=
\left(
n+\displaystyle\frac{1}{n}
\right)
^n
\\\\
a_{n+1}
&=
\left(
n+1+\displaystyle\frac{1}{n+1}
\right)
^{n+1}
\end{align}
$$
形をキレイにして
$$
\begin{align}
a_n
&=
\left(
\displaystyle\frac{n^2+1}{n}
\right)
^n
\\\\
a_{n+1}
&=
\left(
\displaystyle\frac{n^2+2n+2}{n+1}
\right)
^{n+1}
\end{align}
$$
これより
$$
\begin{align}
r
&=
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{a_{n+1}}{a_n}
\\\\&=
\displaystyle\lim_{n \to \infty}
\displaystyle\frac
{\left( \displaystyle\frac{n^2+2n+2}{n+1} \right) ^n}
{\left( \displaystyle\frac{n^2+1}{n} \right) ^n}
\cdot
\displaystyle\frac{n^2+2n+2}{n+1}
\end{align}
$$
ここで左側と右側に分けます。
$$
\begin{align}
r_1
&=
\displaystyle\lim_{n \to \infty}
\displaystyle\frac
{\left( \displaystyle\frac{n^2+2n+2}{n+1} \right) ^n}
{\left( \displaystyle\frac{n^2+1}{n} \right) ^n}
\\\\
r_2
&=
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{n^2+2n+2}{n+1}
\end{align}
$$
それぞれ計算します。
$$
\begin{align}
r_1
&=
\displaystyle\lim_{n \to \infty}
\displaystyle\frac
{\left( \displaystyle\frac{n^2+2n+2}{n+1} \right) ^n}
{\left( \displaystyle\frac{n^2+1}{n} \right) ^n}
\\\\&=
\displaystyle\lim_{n \to \infty}
\left(
\displaystyle\frac{(n^2+2n+2)n}{(n+1)(n^2+1)}
\right)
^n
\\\\&=
\displaystyle\lim_{n \to \infty}
\left(
1+\displaystyle\frac{n^2+n-1}{n^3+n^2+n+1}
\right)
^n
\\\\&=
\displaystyle\lim_{n \to \infty}
\left\{
\left(
1+\displaystyle\frac{n^2+n-1}{n^3+n^2+n+1}
\right)
^{\frac{n^3+n^2+n+1}{n^2+n-1}}
\right\}
^{\frac{n(n^2+n-1)}{n^3+n^2+n+1}}
\\\\&=
\displaystyle\lim_{n \to \infty}
e
^{\frac{n(n^2+n-1)}{n^3+n^2+n+1}}
\\\\&=
e
\end{align}
$$
$$
\begin{align}
r_2
&=
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{n^2+2n+2}{n+1}
\\\\&=
\infty
\end{align}
$$
以上の結果を用いて
$$
\begin{align}
r
&=
r_1 \cdot r_2
\\\\&=
e \cdot \infty
\\\\&=
\infty
\end{align}
$$
$1 < r$のときに当てはまるので発散します。
例題4
$$
\displaystyle\sum_{n=1}^\infty
\displaystyle\frac{1}{n^2}
$$
まずは$a_n$から$a_{n+1}$の形を求めます。
$$
\begin{align}
a_n
&=
\displaystyle\frac{1}{n^2}
\\\\
a_{n+1}
&=
\displaystyle\frac{1}{n^2+2n+1}
\end{align}
$$
これより
$$
\begin{align}
r
&=
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{a_{n+1}}{a_n}
\\\\&=
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{n^2}{n^2+2n+1}
\\\\&=
1
\end{align}
$$
$r=1$のときにあてはまるので判定不能です。
コーシーの収束判定法
$$
r
=
\displaystyle\lim_{n \to \infty}
\sqrt[n]{a_n}
$$
としたとき正項級数$\displaystyle\sum_{n=1}^\infty a_n$は
- $0 \leq r <1$のとき収束
- $r=1$のとき判定不能
- $1 < r$のとき発散
となります。
ダランベールの収束判定法で解いた例題3をコーシーの収束判定法で解いてみます。
$$
\displaystyle\sum_{n=1}^\infty
\left(
n+\displaystyle\frac{1}{n}
\right)
^n
$$
まずは$a_n$から$\sqrt[n]{a_n}$の形を求めます。
$$
\begin{align}
a_n
&=
\left(
n+\displaystyle\frac{1}{n}
\right)
^n
\\\\
\sqrt[n]{a_n}
&=
n+\displaystyle\frac{1}{n}
\end{align}
$$
これより
$$
\begin{align}
r
&=
\displaystyle\lim_{n \to \infty}
\sqrt[n]{a_n}
\\\\&=
\displaystyle\lim_{n \to \infty}
n+\displaystyle\frac{1}{n}
\\\\&=
\infty
\end{align}
$$
$1 < r$のときに当てはまるので発散します。
ダランベールで解いたときに比べて計算量が激減しました。
このように収束判定法はそれぞれ得意な形と不得意な形があるので、どの収束判定法で攻めるかを選ぶときに注意しましょう。
コーシーの収束判定法では$n$乗根をとるので、元々の数列が$n$乗されているときはコーシーを選ぶのがオススメです。
ラーベの収束判定法
$$
r
=
\displaystyle\lim_{n \to \infty}
n
\left(
\displaystyle\frac{a_{n+1}}{a_n}-1
\right)
$$
としたとき正項級数$\displaystyle\sum_{n=1}^\infty a_n$は
- $r < -1$のとき収束
- $r=-1$のとき判定不能
- $-1 < r$のとき発散
となります。
ダランベールの収束判定法で解いた例題4をラーベの収束判定法で解いてみます。
$$
\displaystyle\sum_{n=1}^\infty
\displaystyle\frac{1}{n^2}
$$
まずは$a_n$から$a_{n+1}$の形を求めます。
$$
\begin{align}
a_n
&=
\displaystyle\frac{1}{n^2}
\\\\
a_{n+1}
&=
\displaystyle\frac{1}{n^2+2n+1}
\end{align}
$$
これより
$$
\begin{align}
r
&=
\displaystyle\lim_{n \to \infty}
n
\left(
\displaystyle\frac{a_{n+1}}{a_n}-1
\right)
\\\\&=
\displaystyle\lim_{n \to \infty}
n
\left(
\displaystyle\frac{n^2}{n^2+2n+1}-1
\right)
\\\\&=
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{-2n^2-n}{n^2+2n+1}
\\\\&=
-2
\end{align}
$$
$r < -1$のときに当てはまるので収束します。
ダランベールで解いたときは判定不能でしたが、ラーベで解いたら判定できました。
収束判定法は得意な形と不得意な形があります。
ある収束判定法では判定不能でも他の収束判定法で判定できる場合もあるので、判定不能のときは他の収束判定法を試しましょう。
収束判定法では判定できない具体例
3つの判定法を試して全て判定不能になってしまった場合、自力で収束するかどうかを判定しないといけません。
収束判定法では判定できない無限級数の具体例を2つ挙げます。どちらも$\log(1+x)$をマクローリン展開をするときに収束判定が必要になる無限級数です。
$$
\begin{array}{cl}
(1) &
1-\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}-\displaystyle\frac{1}{4}+\displaystyle\frac{1}{5}-\cdots
\\\\
(2) &
-1-\displaystyle\frac{1}{2}-\displaystyle\frac{1}{3}-\displaystyle\frac{1}{4}-\displaystyle\frac{1}{5}\cdots
\end{array}
$$
この数列はどちらも収束判定法を使うために絶対値を取ると
$$
1+\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}+\displaystyle\frac{1}{4}+\displaystyle\frac{1}{5}+\cdots+\displaystyle\frac{1}{n}+\cdots
$$
となるので、無限級数は
$$
\displaystyle\sum_{n=1}^\infty
\displaystyle\frac{1}{n}
$$
です。これは3つの判定法どれを使っても判定不能になります。
それぞれ個別に判定していきましょう。
具体例1
$$
1-\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}-\displaystyle\frac{1}{4}+\displaystyle\frac{1}{5}-\cdots
$$
最初に偶数項までの和$S_{2n}$を求めます。
$$
\begin{align}
S_{2n}
&=
1-\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}-\displaystyle\frac{1}{4}+\cdots+\displaystyle\frac{1}{2n-1}-\displaystyle\frac{1}{2n}
\\\\&=
1+\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}+\displaystyle\frac{1}{4}+\cdots+\displaystyle\frac{1}{2n-1}+\displaystyle\frac{1}{2n}
-2\left(
\displaystyle\frac{1}{2}+\displaystyle\frac{1}{4}+\cdots+\displaystyle\frac{1}{2n}
\right)
\\\\&=
1+\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}+\displaystyle\frac{1}{4}+\cdots+\displaystyle\frac{1}{2n-1}+\displaystyle\frac{1}{2n}
-\left(
1+\displaystyle\frac{1}{2}+\cdots+\displaystyle\frac{1}{n}
\right)
\\\\&=
\displaystyle\frac{1}{n+1}+\displaystyle\frac{1}{n+2}+\cdots+\displaystyle\frac{1}{2n-1}+\displaystyle\frac{1}{2n}
\\\\&=
\displaystyle\sum_{k=1}^n
\displaystyle\frac{1}{n+k}
\end{align}
$$
$S_{2n}$が求まったので$n\to\infty$とします。
$$
\begin{align}
\displaystyle\lim_{n \to \infty}
S_{2n}
&=
\displaystyle\lim_{n \to \infty}
\displaystyle\sum_{k=1}^n
\displaystyle\frac{1}{n+k}
\\\\&=
\displaystyle\lim_{n \to \infty}
\displaystyle\sum_{k=1}^n
\displaystyle\frac{1}{1+\displaystyle\frac{k}{n}}\cdot\displaystyle\frac{1}{n}
\\\\&=
\displaystyle\int_0^1
\displaystyle\frac{1}{1+x}
~dx
\\\\&=
\left[
\log (1+x)
\right]_0^1
\\\\&=
\log 2
\end{align}
$$
区分求積法を使って計算しました。
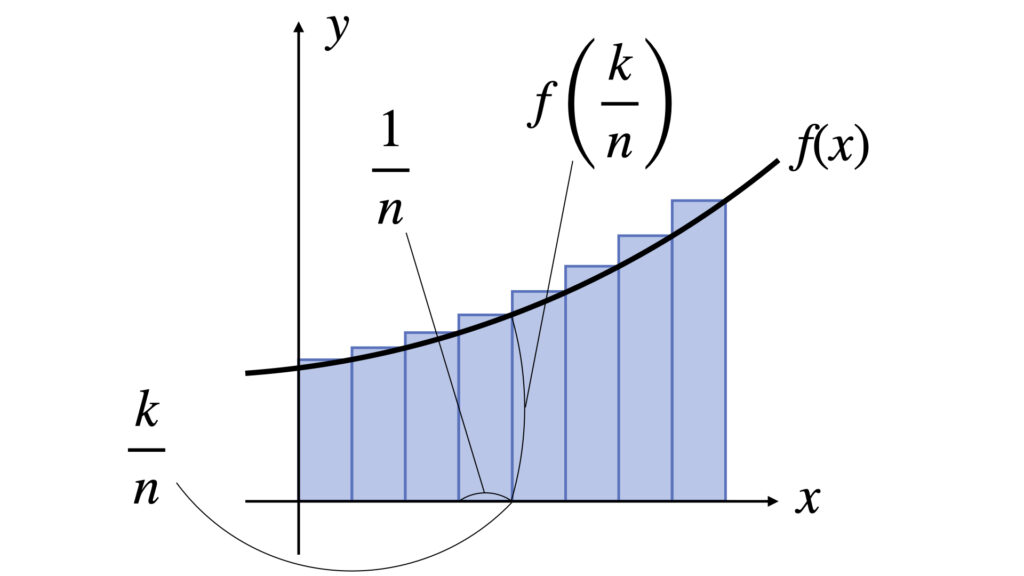
区分求積法は以下の公式です。
$$
\displaystyle\lim_{n \to \infty}
\displaystyle\sum_{k=1}^n
f
\left(
\displaystyle\frac{k}{n}
\right)
\cdot
\displaystyle\frac{1}{n}
=
\displaystyle\int_0^1
f(x)
~dx
$$
画像を見ながらだと式の意味が分かりやすいと思います。
偶数項の和が求まったので、次は奇数項の和$S_{2n+1}$を求めます。
$$
S_{2n+1}=S_{2n}+\displaystyle\frac{1}{2n+1}
$$
両辺$n\to\infty$として
$$
\begin{align}
\displaystyle\lim_{n \to \infty}
S_{2n+1}
&=
\displaystyle\lim_{n \to \infty}
S_{2n}
+
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{1}{2n+1}
\\\\&=
\log 2 + 0
\\\\&=
\log 2
\end{align}
$$
以上よりこの数列の無限級数$S$は
$$
S=\log 2
$$
となり収束します。
具体例2
$$
-1-\displaystyle\frac{1}{2}-\displaystyle\frac{1}{3}-\displaystyle\frac{1}{4}-\displaystyle\frac{1}{5}-\cdots
$$
マイナスのままだと計算しにくいので、いったんプラスに変更して求めます。
$$
1+\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}+\displaystyle\frac{1}{4}+\displaystyle\frac{1}{5}+\cdots
$$
一つ一つの項を四角形の面積だと捉えて、以下のように配置します。

青の四角形の面積の総和が、無限級数の値と一致します。
次に、それぞれの四角形の左上の座標を通る関数を表すと以下のようになります。
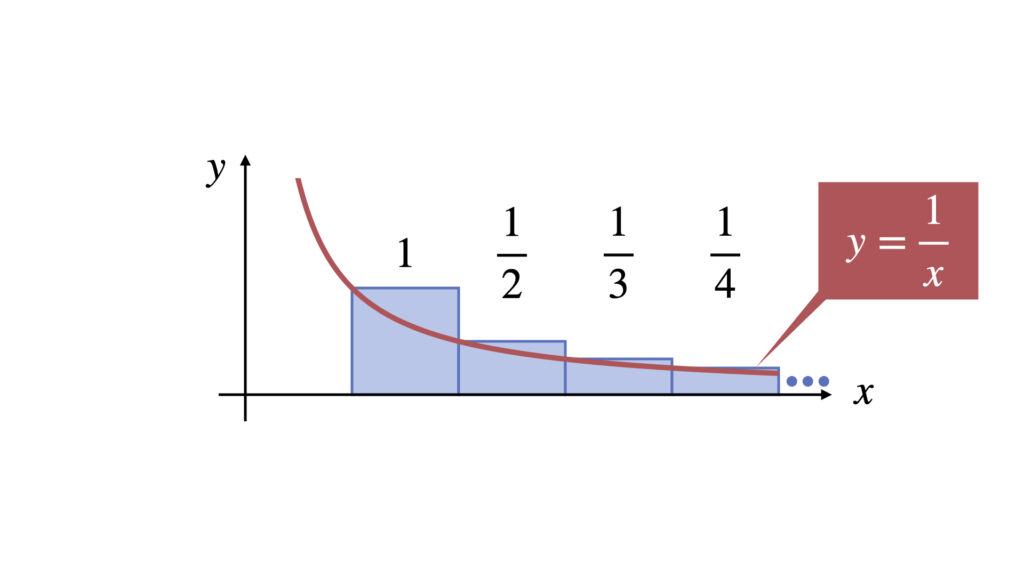
それぞれ面積を比較すると青の面積のほうが赤の面積より大きくなります。
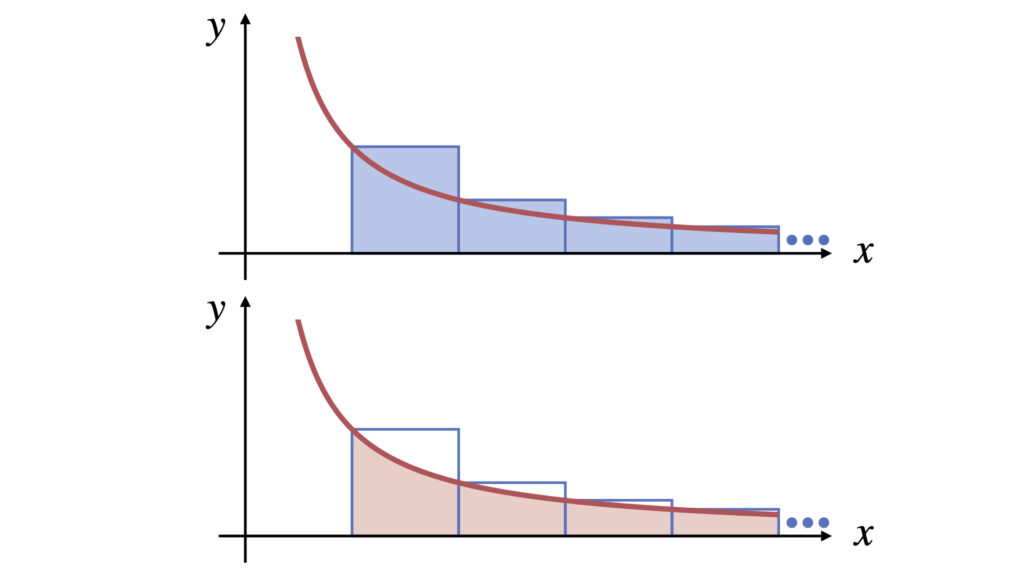
赤の面積を積分で求めると
$$
\begin{align}
\displaystyle\lim_{n \to \infty}
\displaystyle\int_1^n
\displaystyle\frac{1}{x}
~dx
&=
\displaystyle\lim_{n \to \infty}
\left[
\log x
\right]_1^n
\\\\&=
\displaystyle\lim_{n \to \infty}
\log n
\\\\&=
\infty
\end{align}
$$
これより赤の面積は発散です。青の面積は赤の面積より大きいので、青の面積も発散です。
青の面積と無限級数の値が等しいので
$$
1+\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}+\displaystyle\frac{1}{4}+\displaystyle\frac{1}{5}+\cdots
$$
この無限級数は正の無限大に発散します。
したがって、符号を変える前の
$$
-1-\displaystyle\frac{1}{2}-\displaystyle\frac{1}{3}-\displaystyle\frac{1}{4}-\displaystyle\frac{1}{5}-\cdots
$$
この無限級数は負の無限大に発散します。
$$
1+\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}+\displaystyle\frac{1}{4}+\displaystyle\frac{1}{5}+\cdots+\displaystyle\frac{1}{n}+\cdots
$$
この無限級数は調和級数という名前がついています。非常に遅く発散することで有名です。
まとめ
無限級数が求められない場合、収束判定法を使えば収束するかどうかを判定することができます。




コメント欄