こんにちはコーヤです。
このページでは、数列の一般項から極限を求める計算方法を勉強します。数列の振る舞い4パターンを判断しましょう。
数列の極限の振る舞い4パターン
数列の極限の振る舞いは4パターンあります。
- ある定数に収束する
- 振動する
- 正の無限大に発散する
- 負の無限大に発散する
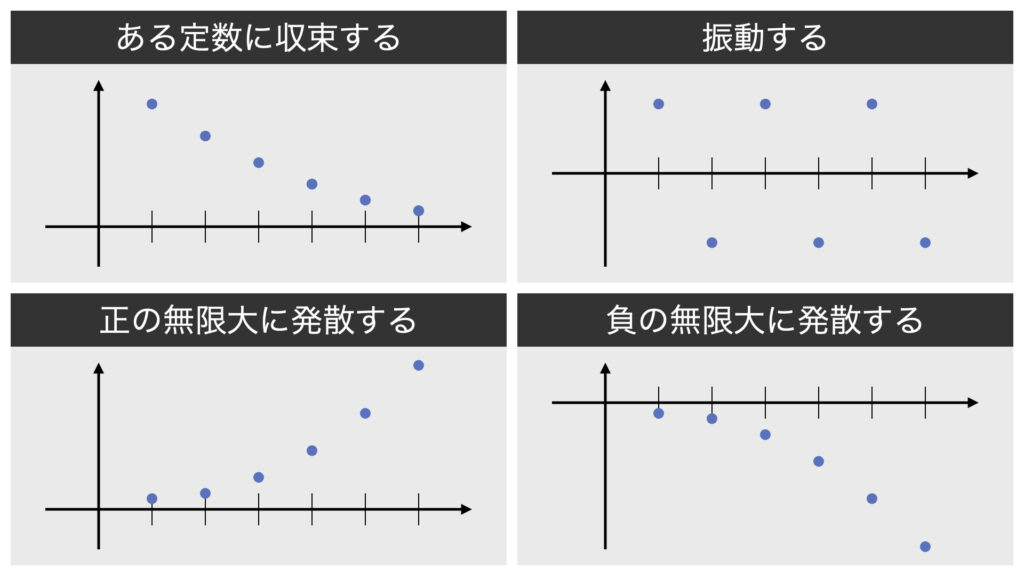
この4パターンのどれに分類されるかを求めていきましょう。
関数の収束発散の速度
関数それぞれの発散の速度から極限を予想することができます。
「階乗関数>指数関数>べき関数>対数関数」という下のグラフのようなイメージで極限が予測できます。
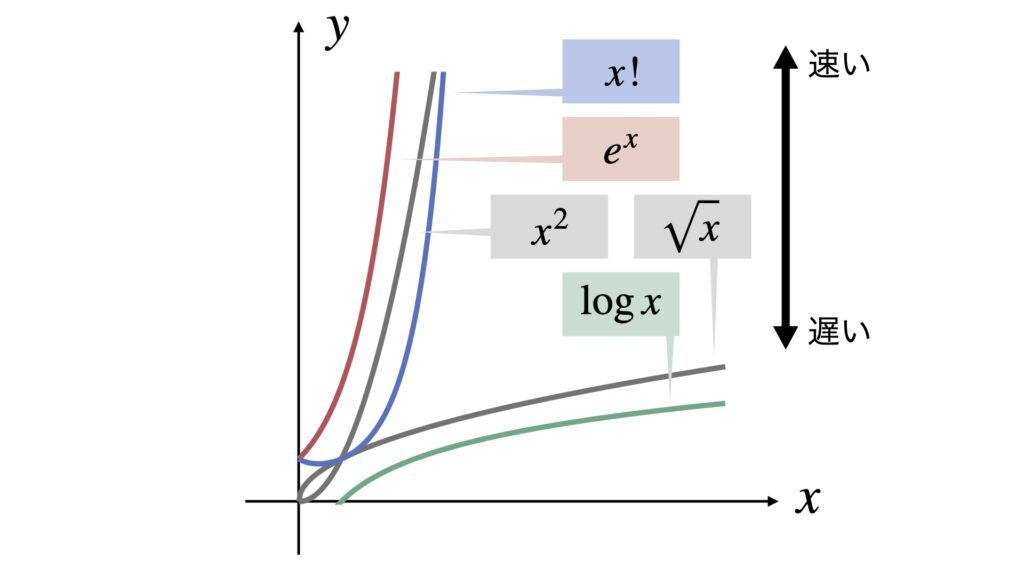
極限の四則演算
2つの数列$a_n,b_n$がそれぞれ$\alpha , \beta$に収束する時、四則演算が成り立ちます。
$$
\begin{array}{cl}
(1) & a_n+b_n = \alpha + \beta \\\\
(2) & a_n-b_n = \alpha -\beta \\\\
(3) & a_n b_n = \alpha \beta \\\\
(4) & \displaystyle\frac{a_n}{b_n} = \displaystyle\frac{\alpha}{\beta}
\end{array}
$$
不等式の利用
不等式の利用は「はさみうち」と「追い出し」の2パターンがあります。
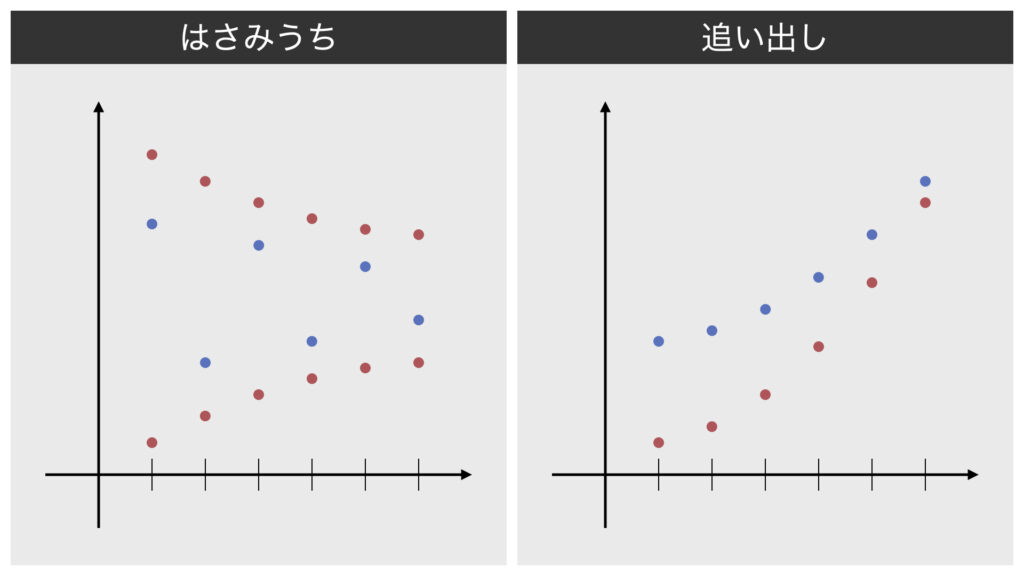
はさみうちは青の数列の上下を囲うような赤の数列を用意し、赤の数列が両方とも同じ値に収束するなら青の数列も同じ値に収束するという考え方です。
追い出しは青の数列の下側になるような赤の数列を用意し、赤の数列が正の無限大に発散するなら青の数列も正の無限大に発散するという考え方です。(負の無限大も同じ考え方で追い出しが使えます。)
数列の極限の例題
それでは例題6つで数列の極限を計算してみましょう。
式変形で極限を直接求めるか、不等式を利用して極限を間接的に求めるかの2択です。
例題1
$$
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{n^2+2n+3}{3n^2+2n+1}
$$
分母分子ともに$n^2$で割ります。
$$
\begin{align}
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{n^2+2n+3}{3n^2+2n+1}
&=
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{1+2\displaystyle\frac{1}{n}+3\displaystyle\frac{1}{n^2}}{3+2\displaystyle\frac{1}{n}+\displaystyle\frac{1}{n^2}}
\\\\&=
\displaystyle\frac{1}{3}
\end{align}
$$
例題2
$$
\displaystyle\lim_{n \to \infty}
\log (n-1)-\log(n+1)
$$
対数関数を1つにまとめると分数になります。
$$
\log (n-1)-\log(n+1)
=
\log
\left(
\displaystyle\frac{n-1}{n+1}
\right)
$$
分母分子ともに$n$で割ります。
$$
\begin{align}
\displaystyle\lim_{n \to \infty}
\log
\left(
\displaystyle\frac{n-1}{n+1}
\right)
&=
\displaystyle\lim_{n \to \infty}
\log
\left(
\displaystyle\frac{1-\displaystyle\frac{1}{n}}{1+\displaystyle\frac{1}{n}}
\right)
\\\\&=
\log 1
\\\\&=
0
\end{align}
$$
例題3
$$
\displaystyle\lim_{n \to \infty}
n\left(\sqrt{n^2+1}-\sqrt{n^2-1}\right)
$$
ルートがあるときは有理化すると計算が進みます。
$$
n\left(\sqrt{n^2+1}-\sqrt{n^2-1}\right)
=
\displaystyle\frac{2n}
{\sqrt{n^2+1}+\sqrt{n^2-1}}
$$
分母分子を割るパターンが使えます。分母分子ともに$n$で割ります。
$$
\begin{align}
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{2n}
{\sqrt{n^2+1}+\sqrt{n^2-1}}
&=
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{2}
{\sqrt{1+\displaystyle\frac{1}{n^2}}+\sqrt{1-\displaystyle\frac{1}{n^2}}}
\\\\&=
\displaystyle\frac{2}{1+1}
\\\\&=
1
\end{align}
$$
例題4
$$
\displaystyle\lim_{n \to \infty}
e^{\cos(n\pi)}
$$
$\cos(n\pi)=(-1)^n$です。この数列を$n=1$から順に書き出してみると
$$
\begin{array}{ccccccc}
\displaystyle\frac{1}{e},&e,&\displaystyle\frac{1}{e},&e,&\displaystyle\frac{1}{e},&e,&\cdots
\end{array}
$$
このように振動しています。振動の場合は極限なしです。
例題5
$$
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{\cos(n\pi)}{n}
$$
$\cos(n\pi)$があるので振動しそうですが、分母に$n$があるため収束すると予想できます。
このような振動を伴いつつ収束しそうな数列は「はさみうち」を使うことで計算できます。
$$
-1
\leq
\cos(n\pi)
\leq
1
$$
振動する部分を最大値と最小値で「はさみうち」します。不等式全体を$n$で割って
$$
-\displaystyle\frac{1}{n}
\leq
\displaystyle\frac{\cos(n\pi)}{n}
\leq
\displaystyle\frac{1}{n}
$$
続いて$n\to\infty$とします。
$$
\displaystyle\lim_{n \to \infty}
-\displaystyle\frac{1}{n}
\leq
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{\cos(n\pi)}{n}
\leq
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{1}{n}
$$
両サイドの極限は
$$
\displaystyle\lim_{n \to \infty}
-\displaystyle\frac{1}{n}
=
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{1}{n}
=
0
$$
これより
$$
0
\leq
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{\cos(n\pi)}{n}
\leq
0
$$
となるので
$$
\displaystyle\lim_{n \to \infty}
\displaystyle\frac{\cos(n\pi)}{n}
=
0
$$
です。
例題6
$$
\displaystyle\lim_{n \to \infty}
3^n-2^n
$$
$3^n$でくくって
$$
\displaystyle\lim_{n \to \infty}
3^n-2^n
=
\displaystyle\lim_{n \to \infty}
3^n
\left\{
1-
\left(
\displaystyle\frac{2}{3}
\right)
^n
\right\}
$$
この時点で無限に発散する予測がつきます。この数列より小さな数列を用意して「追い出し」を使いましょう。
$$
1-
\left(
\displaystyle\frac{2}{3}
\right)
^n
\geq
\displaystyle\frac{1}{3}
$$
この不等式を利用して
$$
\displaystyle\lim_{n \to \infty}
3^n
\left\{
1-
\left(
\displaystyle\frac{2}{3}
\right)
^n
\right\}
\geq
\displaystyle\lim_{n \to \infty}
3^n
\left\{
\displaystyle\frac{1}{3}
\right\}
$$
となります。
$$
\displaystyle\lim_{n \to \infty}
3^n
\left\{
\displaystyle\frac{1}{3}
\right\}
=
\displaystyle\lim_{n \to \infty}
3^{n-1}
=
\infty
$$
小さい数列ですら無限大に発散することが分かったので
$$
\displaystyle\lim_{n \to \infty}
3^n-2^n
=
\infty
$$
です。
まとめ
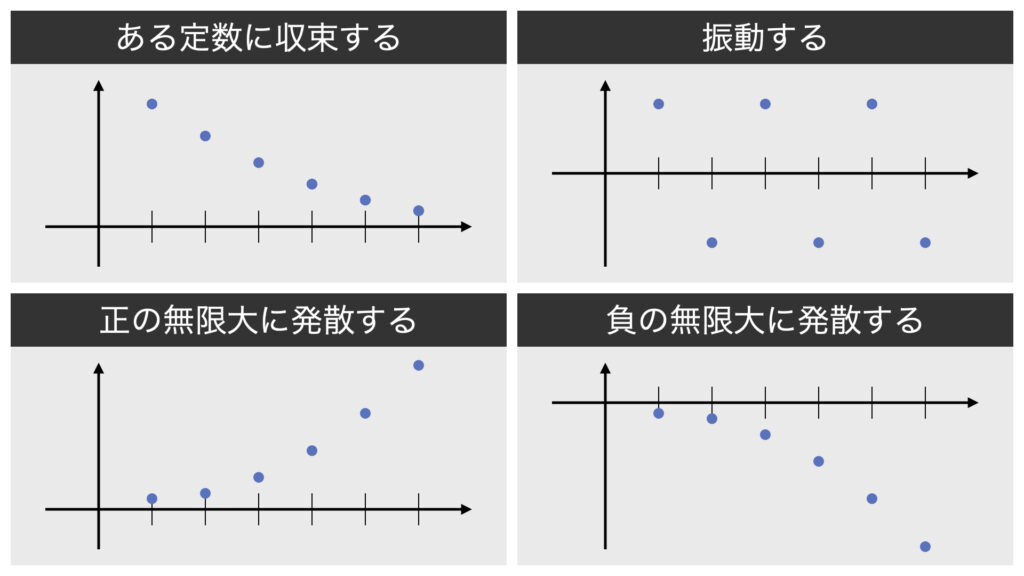
数列の極限の振る舞いは4パターンあります。
- ある定数に収束する
- 振動する
- 正の無限大に発散する
- 負の無限大に発散する




コメント欄