こんにちはコーヤです。
このページでは、双曲線関数の性質を勉強します。三角関数の公式と混乱しないように注意が必要です。
双曲線関数の定義
双曲線関数は以下のように定義された関数です。
$$
\begin{align}
\sinh x =
\displaystyle\frac{e^x-e^{-x}}{2}
\\\\
\cosh x =
\displaystyle\frac{e^x+e^{-x}}{2}
\\\\
\tanh x =
\displaystyle\frac{e^x-e^{-x}}{e^x+e^{-x}}
\end{align}
$$
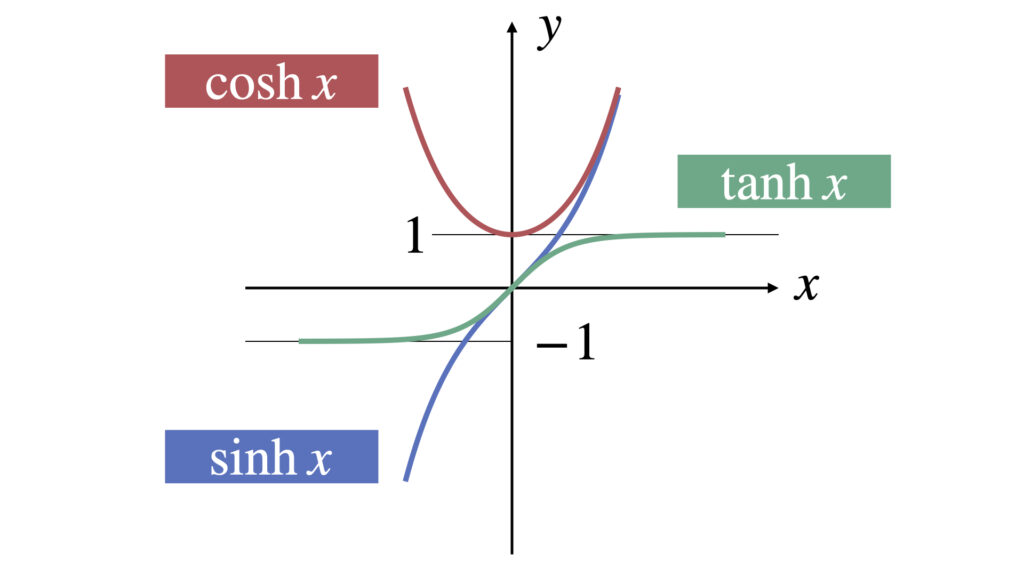
グラフはそれぞれ以下のようになります。

双曲線関数の性質
双曲線関数の定義は指数関数の式でしたが、性質は三角関数とそっくりです。
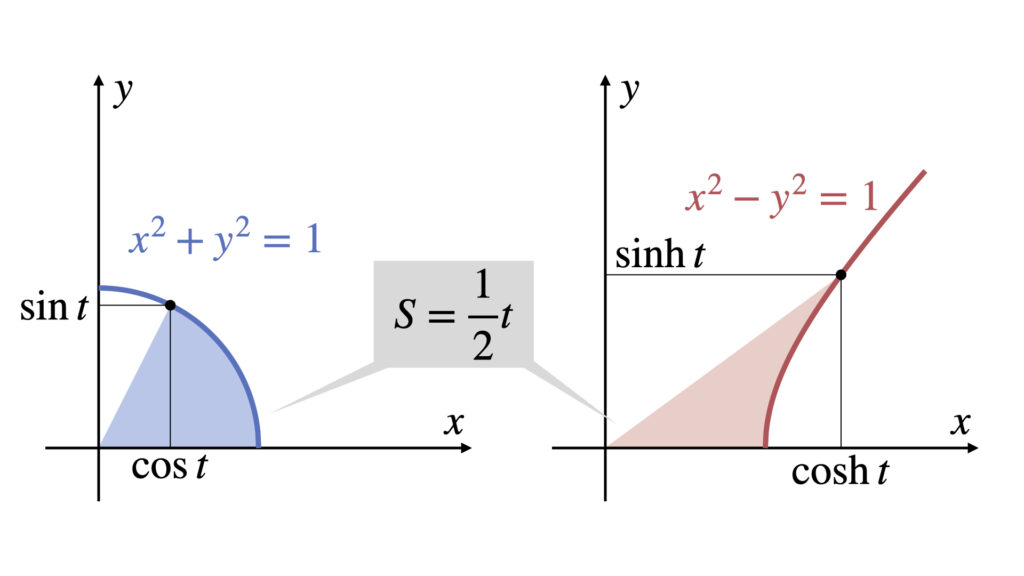
点$(\cos t,\sin t)$は線$x^2+y^2=1$上に位置します。
点$(\cosh t,\sinh t)$は線$x^2-y^2=1$上に位置します。
どちらも色がついている部分の面積は$\displaystyle\frac{1}{2}t$です。
双曲線関数の公式
双曲線関数は公式も三角関数の公式にそっくりですが符号が異なります。
符号ミスが頻発するので、公式を使うときは前述の定義を代入して成立しているか確認するのがオススメです。
相互関係
$$
\cosh ^2 x-\sinh ^2 x =1
$$
$$
\tanh x=\displaystyle\frac{\sinh x}{\cosh x}
$$
$$
1-\tanh ^2 x=\displaystyle\frac{1}{\cosh ^2 x}
$$
加法定理
$$
\sinh(\alpha\pm\beta)
=
\sinh\alpha\cosh\beta\pm\cosh\alpha\sinh\beta
$$
$$
\cosh(\alpha\pm\beta)
=
\cosh\alpha\cosh\beta\pm\sinh\alpha\sinh\beta
$$
$$
\tanh(\alpha\pm\beta)
=
\displaystyle\frac{\tanh\alpha\pm\tanh\beta}{1\pm\tanh\alpha\tanh\beta}
$$
倍角の公式
$$
\sinh 2x
=
2\sinh x\cosh x
$$
$$
\begin{align}
\cosh 2x
&=
\cosh ^2 x+\sinh ^2 x
\\\\&=
2\cosh ^2 x-1
\\\\&=
1+2\sinh ^2 x
\end{align}
$$
$$
\tanh 2x
=
\displaystyle\frac{2\tanh x}{1+\tanh ^2 x}
$$
半角の公式
$$
\sinh ^2 x
=
\displaystyle\frac{\cosh 2x-1}{2}
$$
$$
\cosh ^2 x
=
\displaystyle\frac{\cosh 2x+1}{2}
$$
$$
\tanh ^2 x
=
\displaystyle\frac{\cosh 2x-1}{\cosh 2x+1}
$$
微分積分
$$
(\sinh x)’
=
\cosh x
$$
$$
(\cosh x)’
=
\sinh x
$$
$$
(\tanh x)’
=
\displaystyle\frac{1}{\cosh ^2 x}
$$
$$
\displaystyle\int
\sinh x
~dx
=
\cosh x +C
$$
$$
\displaystyle\int
\cosh x
~dx
=
\sinh x +C
$$
$$
\displaystyle\int
\tanh x
~dx
=
\log(\cosh x) +C
$$
逆双曲線関数の性質
三角関数に逆三角関数があったように、双曲線関数には逆双曲線関数があります。

逆三角関数には”arc”がつきましたが、逆双曲線関数は”ar”がつきます。
Wikipediaによると”arc”の語源はarcus(弓)で”ar”の語源はarea(面積)とのことです。
arsinh
$$
\mathrm{arsinh}\, x
=
\log
\left(
x+\sqrt{x^2+1}
\right)
$$
導出
$$
y
=
\sinh x
=
\displaystyle\frac{e^x-e^{-x}}{2}
$$
双曲線関数の$x$と$y$を入れ替えて
$$
x
=
\displaystyle\frac{e^y-e^{-y}}{2}
$$
これを整理して
$$
e^{2y}-2xe^y-1=0
$$
解の公式より
$$
e^y
=
x+\sqrt{x^2+1}
$$
となります。
解の公式の結果はプラマイではなくプラスだけです。
指数関数の値は必ず正のため$e^y > 0$となります。
右辺の項を比べると$x<\sqrt{x^2+1}$が成り立ちます。
よって解の公式のマイナスは不適です。
両辺対数をとって
$$
y
=
\log
\left(
x+\sqrt{x^2+1}
\right)
$$
となり逆関数が求まりました。
arcosh
$$
\mathrm{arcosh}\, x
=
\log
\left(
x+\sqrt{x^2-1}
\right)
$$
導出
$y=\cosh x$は1対2対応の関数であるため、グラフの実線の部分だけ考えます。

$$
y
=
\cosh x
=
\displaystyle\frac{e^x+e^{-x}}{2}
$$
双曲線関数の$x$と$y$を入れ替えて
$$
x
=
\displaystyle\frac{e^y+e^{-y}}{2}
$$
これを整理して
$$
e^{2y}-2xe^y+1=0
$$
解の公式より
$$
e^y
=
x+\sqrt{x^2-1}
$$
となります。
解の公式の結果はプラマイではなくプラスだけです。
元の関数$\cosh x$の範囲が$x \geq 0$かつ$y \geq 1$なので、逆関数$\mathrm{arcosh}\, x$の範囲は$x \geq 1$かつ$y \geq 0$となります。
$y \geq 0$ということは$e^y \geq 1$になります。
つまり$x \geq 1$の範囲で$e^y \geq 1$を満たすような解しか条件に当てはまりません。
よって解の公式のマイナスは不適です。
両辺対数をとって
$$
y
=
\log
\left(
x+\sqrt{x^2-1}
\right)
$$
となり逆関数が求まりました。
ちなみにグラフの点線の部分は
$$
y
=
\log
\left(
x-\sqrt{x^2-1}
\right)
$$
です。実線と点線を両方合わせて
$$
y
=
\log
\left(
x\pm\sqrt{x^2-1}
\right)
$$
これを$\mathrm{arcosh}\, x$とすることもあるようです。
artanh
$$
\mathrm{artanh}\, x
=
\displaystyle\frac{1}{2}
\log
\displaystyle\frac{1+x}{1-x}
$$
導出
$$
y
=
\tanh x
=
\displaystyle\frac{e^x-e^{-x}}{e^x+e^{-x}}
$$
双曲線関数の$x$と$y$を入れ替えて
$$
\begin{align}
x
&=
\displaystyle\frac{e^y-e^{-y}}{e^y+e^{-y}}
\\\\&=
\displaystyle\frac{e^{2y}-1}{e^{2y}+1}
\end{align}
$$
これを整理して
$$
e^{2y}
=
\displaystyle\frac{1+x}{1-x}
$$
両辺対数をとって
$$
2y
=
\log
\displaystyle\frac{1+x}{1-x}
$$
よって
$$
y
=
\displaystyle\frac{1}{2}
\log
\displaystyle\frac{1+x}{1-x}
$$
となり逆関数が求まりました。
双曲線関数の例題
双曲線関数の登場で置換積分の幅が広がります。
それでは例題2つで置換積分をやってみましょう。
例題1
$$
\displaystyle\int
\displaystyle\frac{1}{\sqrt{1+x^2}}
~dx
$$
$x=\sinh t$と置換します。
$$
\begin{align}
\displaystyle\int
\displaystyle\frac{1}{\sqrt{1+x^2}}
~dx
&=
\displaystyle\int
\displaystyle\frac{1}{\sqrt{1+\sinh ^2 t}}\cosh t
~dt
\\\\&=
\displaystyle\int
\displaystyle\frac{\cosh t}{\cosh t}
~dt
\\\\&=
t+C
\\\\&=
\mathrm{arsinh}\,t+C
\\\\&=
\log
\left(
x+\sqrt{x^2+1}
\right)
+C
\end{align}
$$
例題2
$$
\displaystyle\int
\sqrt{1+x^2}
~dx
$$
$x=\sinh t$と置換します。
$$
\begin{align}
\displaystyle\int
\sqrt{1+x^2}
~dx
&=
\displaystyle\int
\sqrt{1+\sinh ^2 t}
\cosh t
~dt
\\\\&=
\displaystyle\int
\cosh ^2 t
~dt
\\\\&=
\displaystyle\int
\displaystyle\frac{\cosh 2t+1}{2}
~dt
\\\\&=
\displaystyle\frac{1}{4}\sinh 2t
+\displaystyle\frac{1}{2}t
+C
\\\\&=
\displaystyle\frac{1}{2}
\left(
\sinh t\cosh t +t
\right)
+C
\end{align}
$$
途中の式変形で半角の公式と倍角の公式を使いました。
ここで$t$の関数から$x$の関数へ戻します。
$$
\begin{align}
\sinh t &= x
\\\\
\cosh t &= \sqrt{1-x^2}
\end{align}
$$
を代入して
$$
\begin{align}
\displaystyle\frac{1}{2}
\left(
\sinh t\cosh t +t
\right)
+C
&=
\displaystyle\frac{1}{2}
\left(
x\sqrt{1-x^2} +\mathrm{arsinh}\,x
\right)
+C
\\\\&=
\displaystyle\frac{1}{2}
\left\{
x\sqrt{1-x^2}
+
\log
\left(
x+\sqrt{x^2+1}
\right)
\right\}
+C
\end{align}
$$
以上より
$$
\displaystyle\int
\sqrt{1+x^2}
~dx
=
\displaystyle\frac{1}{2}
\left\{
x\sqrt{1-x^2}
+
\log
\left(
x+\sqrt{x^2+1}
\right)
\right\}
+C
$$
です。
まとめ
双曲線関数は以下のように定義された関数です。
$$
\begin{align}
\sinh x =
\displaystyle\frac{e^x-e^{-x}}{2}
\\\\
\cosh x =
\displaystyle\frac{e^x+e^{-x}}{2}
\\\\
\tanh x =
\displaystyle\frac{e^x-e^{-x}}{e^x+e^{-x}}
\end{align}
$$




コメント欄