こんにちはコーヤです。
このページでは線形空間の一部分を切り取った部分空間の性質と、部分空間を組み合わせて作る和空間の性質を勉強をします。
部分空間の作り方
線形空間$V$のテキトーな元をいくつか拾ってきて、その元を線形結合したものを部分空間$W$と言います。
線形空間$V$の元$\boldsymbol{a}_1 , \boldsymbol{a}_2 \cdots \boldsymbol{a}_n$と実数$c_1 , c_2 \cdots c_n$を用いて以下のように表されます。
$$
W
=
\left\{
\begin{array}{c|c}
\boldsymbol{w}
&
\boldsymbol{w}
=
c_1\boldsymbol{a}_1 + c_2\boldsymbol{a}_2 + \cdots + c_n\boldsymbol{a}_n
\end{array}
\right\}
$$
式だけだと伝わりにくいので具体例を見ていきます。
例えば線形空間$V$を2次元列ベクトル空間$R^2$だとしてテキトーな元を拾ってきます。
今回は$\boldsymbol{f}_1$を拾ったとします。$\boldsymbol{f}_1$は以下のような元です。
$$
\boldsymbol{f}_1
=
\begin{pmatrix}
2 \\
1
\end{pmatrix}
$$
この$\boldsymbol{f}_1$の線形結合したものが部分空間$F_1$です。
$$
F_1
=
\left\{
\begin{array}{c|c}
\boldsymbol{w}
&
\boldsymbol{w}
=
c_1\boldsymbol{f}_1
\end{array}
\right\}
$$
では$\boldsymbol{w}$がどのような値をとるのか計算していきます。
$$
\boldsymbol{w}
=
\begin{pmatrix}
x \\
y
\end{pmatrix}
$$
とします。
$$
\boldsymbol{w}
=
c_1\boldsymbol{f}_1
$$
を方程式の形に変形して
$$
\begin{align}
x&=2c_1
\\\\
y&=c_1
\end{align}
$$
$c_1$は自由な値が取れるので
$$
x-2y=0
$$
という関係が導けます。
以上より$\boldsymbol{f}_1$がつくる部分空間$F_1$は$x-2y=0$の直線です。
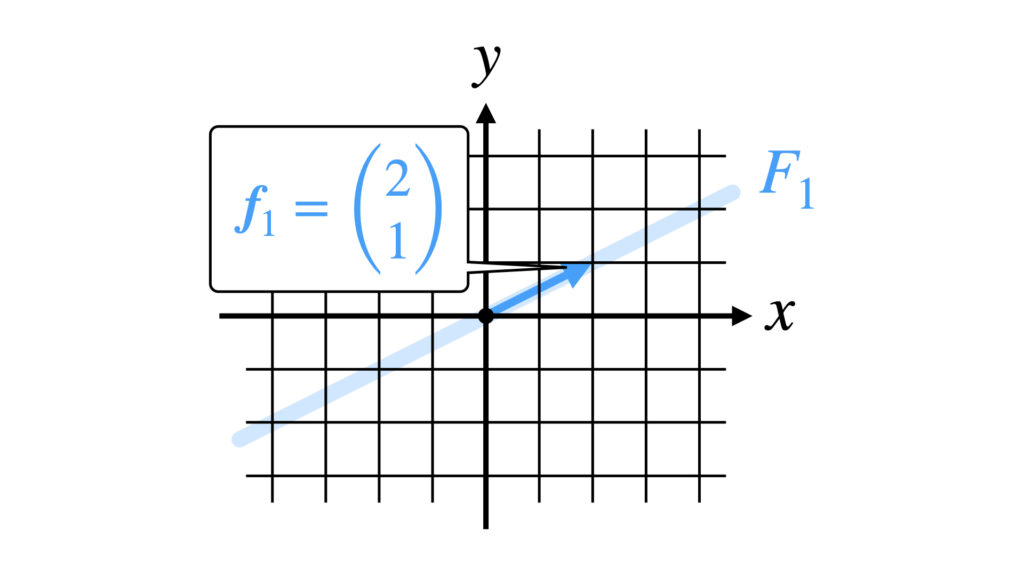
たしかに$F_1$は$\boldsymbol{f}_1$を$c_1$倍した空間になっています。
部分空間の条件
ある空間が部分空間かどうか判断するために確認するべきポイントは1個だけです。
$W$の任意の元$\boldsymbol{b}_1 , \boldsymbol{b}_2$と任意の実数$\lambda , \mu$を用いて
$$
\lambda \boldsymbol{b}_1 + \mu \boldsymbol{b}_2 \in W
$$
が成り立っていればOKです。
それでは$F_1$が本当に部分空間かどうか調べてみます。$F_1$から任意の元を2つ拾ってきます。
$$
\left.
\begin{array}{cc}
\boldsymbol{f}_i
=
\begin{pmatrix}
x_i \\
y_i
\end{pmatrix}
&
\boldsymbol{f}_j
=
\begin{pmatrix}
x_j \\
y_j
\end{pmatrix}
\end{array}
\right.
$$
この2つを拾ってきました。これらは$F_1$から拾ってきた元なので
$$
\begin{align}
x_i-2y_i&=0
\\\\
x_j-2y_j&=0
\end{align}
$$
を満たします。それでは実数$\lambda , \mu$を用いて部分空間かどうか判断します。
$$
\begin{align}
\lambda \boldsymbol{f}_i + \mu \boldsymbol{f}_j
&=
\lambda
\begin{pmatrix}
x_i \\
y_i
\end{pmatrix}
+
\mu
\begin{pmatrix}
x_j \\
y_j
\end{pmatrix}
\\\\&=
\begin{pmatrix}
\lambda x_i + \mu x_j \\
\lambda y_i + \mu y_j
\end{pmatrix}
\end{align}
$$
これが$F_1$に含まれていることが確認できればOKです。$F_1$に含まれてるかどうかは$x-2y=0$の直線状にいるかどうかで確認できます。
$$
\begin{align}
x-2y
&=
( \lambda x_i + \mu x_j)-2 ( \lambda y_i + \mu y_j )
\\\\&=
\lambda ( x_i-2 y_i ) + \mu ( x_j-2 y_j )
\\\\&=
\lambda (0) + \mu (0)
\\\\&=
0
\end{align}
$$
となります。これで$\lambda \boldsymbol{f}_i + \mu \boldsymbol{f}_j \in W$が示せたので$F_1$は部分空間だと証明できました。
部分空間かどうかを判断するとき、いちいち計算するのは面倒なのでよく出る例だけ紹介します。
部分空間の大事なポイントとして
- 原点を通らない空間は部分空間にはなりません。
- 部分空間は元の空間と一致してもOKです。
- 部分空間は零ベクトルだけでも大丈夫です。
以上をふまえて
- 線形空間$R^2$の部分空間は、$R^2$そのもの、原点を通る直線全て、原点、の3種類になります。
- 線形空間$R^3$の部分空間は、$R^3$そのもの、原点を通る平面全て、原点を通る直線全て、原点、の4種類になります。
和空間の作り方と和集合との違い
$R^2$から拾ってきた$\boldsymbol{f}_1$で作った部分空間が$F_1$でした。
$R^2$から別の元$\boldsymbol{f}_2$を拾ってきて、それで作った部分空間を$F_2$とします。
$$
\boldsymbol{f}_2
=
\begin{pmatrix}
1 \\
-1
\end{pmatrix}
$$
とすると部分空間$F_2$は$x+y=0$の直線になります。
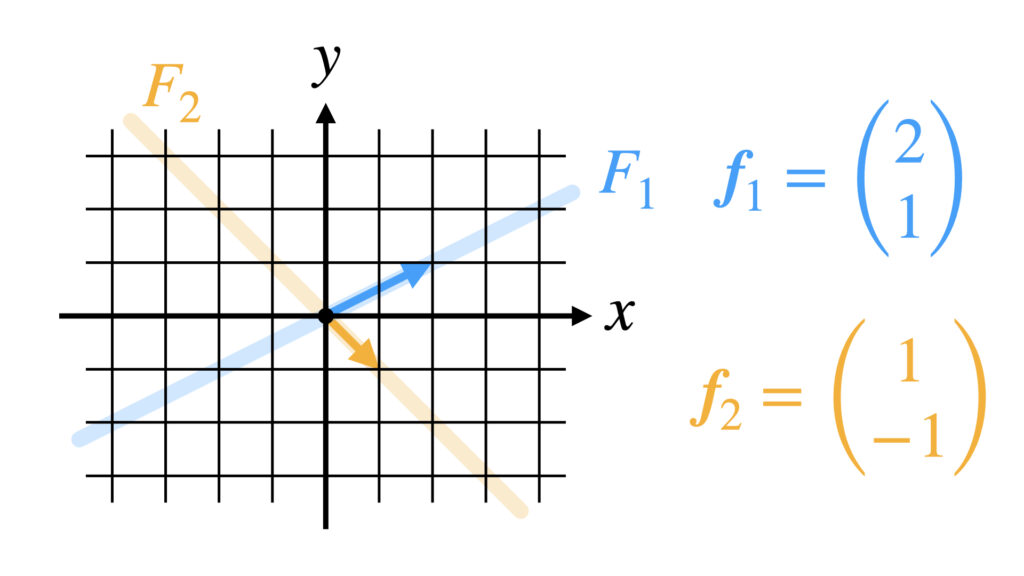
ここで$F_1$と$F_2$の和集合$F_1 \cup F_2$の空間を考えます。$F_1 \cup F_2$は線形空間の性質を満たすでしょうか。
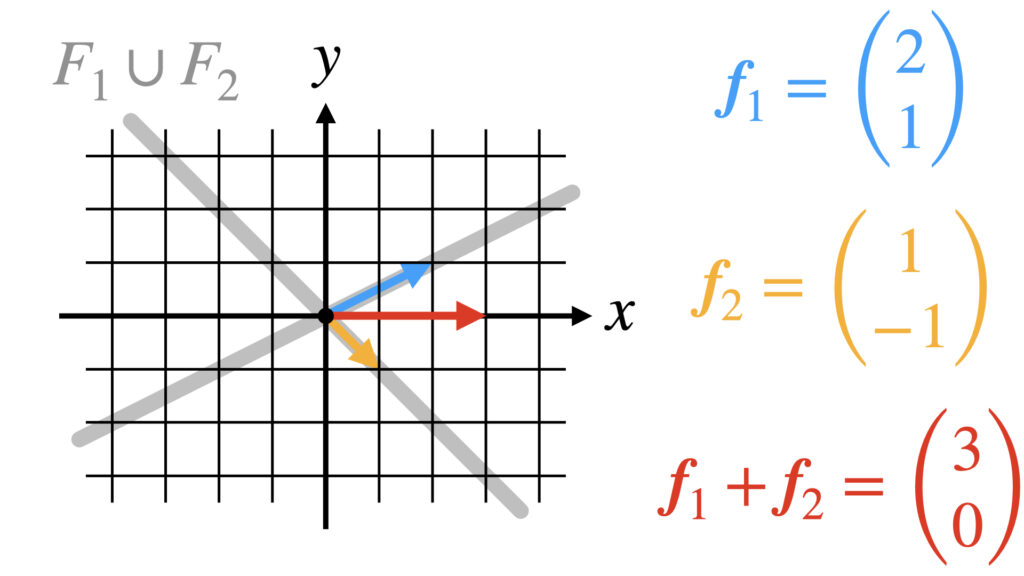
グラフを見ると分かる通り$\boldsymbol{f}_1$も$\boldsymbol{f}_2$も$F_1 \cup F_2$の元ですが、和の演算を行った$\boldsymbol{f}_1+\boldsymbol{f}_2$は$F_1 \cup F_2$の元ではなくなってしまいました。
和の演算が定義できないため$F_1 \cup F_2$は線形空間ではありません。一般的に線形空間の和集合は線形空間ではなくなることが多いです。
これだと困ってしまうので、和集合$F_1 \cup F_2$の代わりに和空間$F_1+F_2$を以下のように定義します。
$$
F_1+F_2
=
\left\{
\begin{array}{c|ccc}
\boldsymbol{r}
&
\boldsymbol{r}=\boldsymbol{p}+\boldsymbol{q},
&
\boldsymbol{p} \in F_1,
&
\boldsymbol{q} \in F_2
\end{array}
\right\}
$$
このように定義すれば和空間は線形空間の性質を満たすうえ、以下の公式まで作れます。
$$
\dim (F_1+F_2)
=
\dim F_1
+\dim F_2
-\dim (F_1 \cap F_2)
$$
今回の例だと$F_1$と$F_2$は直線なので$\dim F_1=\dim F_2=1$です。$F_1 \cap F_2$は$F_1$と$F_2$の積集合なので原点のみです。さっきのグラフを見ても$F_1$と$F_2$が被る部分は原点しかないことが分かります。よって$\dim (F_1 \cap F_2)=0$です。
これを公式に当てはめて$\dim (F_1+F_2)=2$です。$F_1$と$F_2$の和空間は2次元空間だと分かりました。
$F_1+F_2$は$F_1$と$F_2$を含むような2次元空間です。
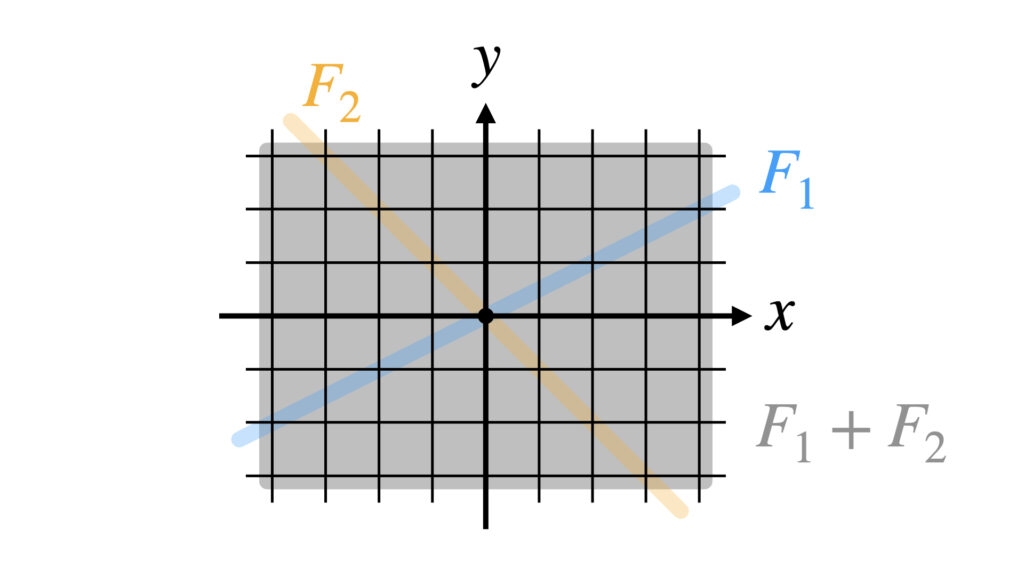
和空間の広げ方
$\boldsymbol{f}_1$で作った部分空間$F_1$と$\boldsymbol{f}_2$で作った部分空間$F_2$について見てきました。
今度は$R^2$の元$\boldsymbol{f}_3$を拾ってきて、部分空間$F_3$を作ります。
$$
\boldsymbol{f}_3
=
\begin{pmatrix}
-1 \\
-2
\end{pmatrix}
$$
とすると部分空間$F_3$は$2x-y=0$の直線になります。
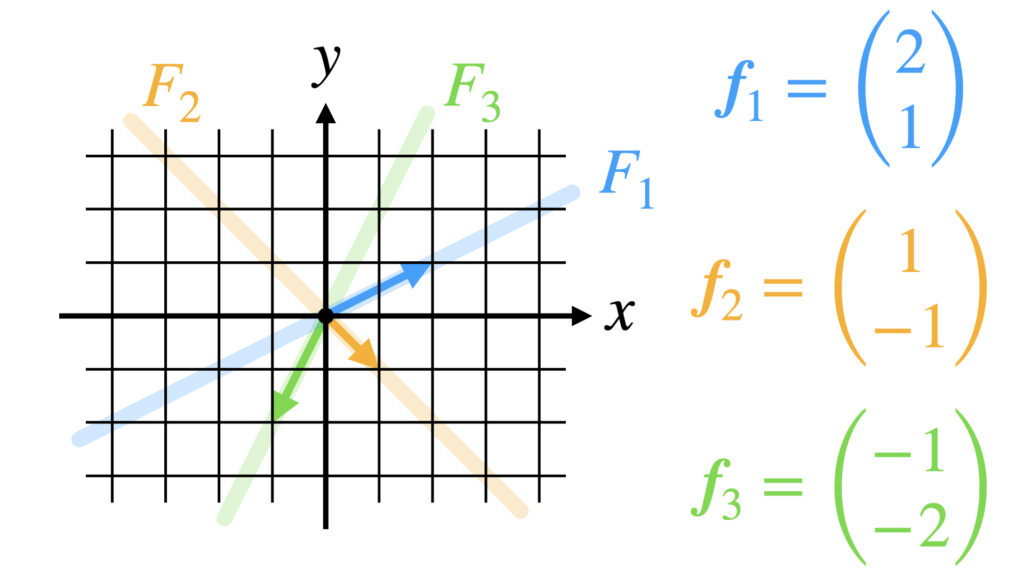
ここで和空間$F_1+F_2+F_3$を考えてみます。
すでに求めている$F_1+F_2$の和空間を$F_{12}$と表します。すると$F_1+F_2+F_3$は$F_{12}+F_3$と表せます。それでは和空間の公式を使って$F_{12}+F_3$の次元を求めます。
$$
\begin{align}
\dim (F_{12}+F_3)
&=
\dim F_{12}
+\dim F_3
-\dim (F_{12} \cap F_3)
\\\\&=
2+1-1
\\&=
2
\end{align}
$$
$F_{12}+F_3$の和空間は2次元空間です。でも$F_{12}$も2次元空間でしたね。足しても足さなくても答えが変わらないので$F_3$を足すのは無意味だったみたいです。
ではここで視点を変えてみます。
1次元空間$F_1,F_2,F_3$の3つが与えられて、これらの和空間が2次元空間になるように式を立ててみます。例えば以下の5式はどうでしょうか?
$$
\begin{array}{cl}
(1) & F_1+F_2\\
(2) & F_1+F_3\\
(3) & F_2+F_3\\
(4) & F_1+F_2+F_3 \\
(5) & F_1+F_1+F_2+F_2+F_3+F_3
\end{array}
$$
5式とも2次元空間になるので正解です。
しかし、さっき計算したとおり(4)式はスマートな表現ではありません。$F_3$を足さなくても2次元空間が作れているので、無駄な計算をわざわざ書いています。
(5)式はあきらかに無駄な計算をしていることが分かります。それでも2次元空間になるので正解となってしまいます。
逆に(1),(2),(3)式は必要最低限で無駄のない表現です。
ここで直和という表現が登場します。無駄のない和空間の広げ方を直和といい、無駄のある和空間の広げ方と区別するために$+$を$\oplus$に変えて表現します。
直和をふまえて5式を書き直すと
$$
\begin{array}{ll}
(1) & F_1 \oplus F_2\\
(2) & F_1 \oplus F_3\\
(3) & F_2 \oplus F_3\\
(4) & F_1+F_2+F_3 \\
(5) & F_1+F_1+F_2+F_2+F_3+F_3
\end{array}
$$
となります。
直和のときは和空間の公式が簡単になります。(1)式を例にすると
$$
\dim (F_1+F_2)
=
\dim F_1
+
\dim F_2
$$
と書き換えることができます。直和のときは積集合の次元が0になるので、引き算の部分がなくなります。
まとめ
線形空間$V$の部分集合かつ線形空間の性質を満たすものを部分空間$W$といいます。
部分空間の足し算を和空間と定義します。無駄のない和空間の広げ方を直和と言います。




コメント欄