テイラー展開の計算方法

こんにちはコーヤです。

このページでは、テイラー展開の計算方法と展開の意味を勉強します。テイラー展開は微分方程式や指数行列など多くの分野で活躍します。

テイラー展開の導出
近似精度の検証
マクローリン展開との関係性
まとめ

テイラー展開の導出

関数$f(x)$と$x=a$で接する接線$l$を考えます。接線$l$は以下の式です。

$$
l:y=f(a)+f'(a)(x-a)
$$

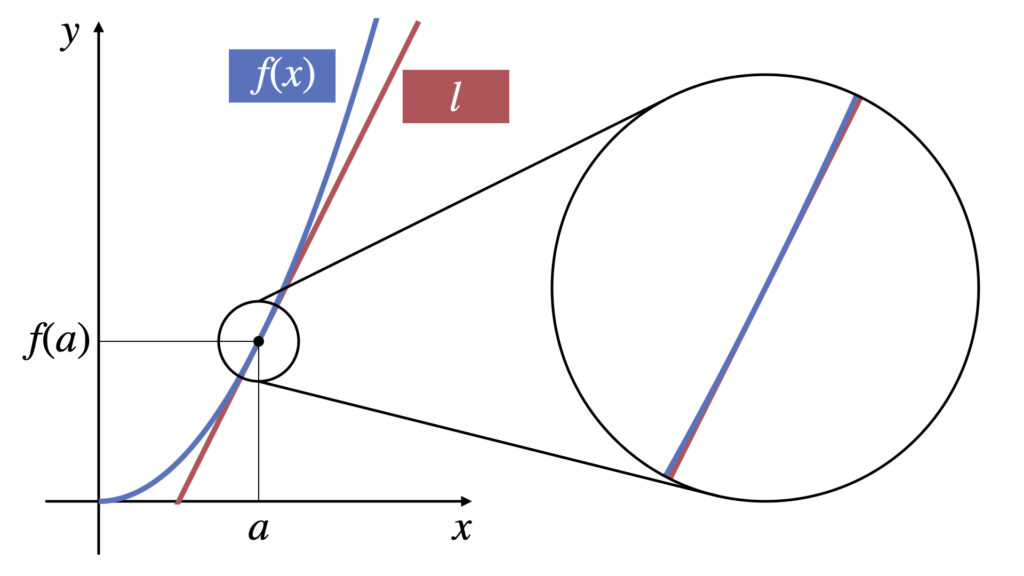
$x=a$の部分を拡大すれば$f(x)$と$l$はほぼ同じ関数とみなすことができます。

$$
f(x)
\simeq
f(a)+f'(a)(x-a)
$$

ですが$f(x)$は曲線なので、直線だけで近似するのは厳しいです。もう少し近似精度を上げるために2次式も追加してみます。

$$
f(x)
\simeq
f(a)+f'(a)(x-a)+px^2+qx+r
\tag{1}
$$

$x=a$付近で式(1)を満たす$p,q,r$を計算しましょう。

両辺を1階微分、2階微分します。

$$
f'(x)
\simeq
f'(a)+2px+q
\tag{2}
$$

$$
f'{}'(x)
\simeq
2p
\tag{3}
$$

式(1)(2)(3)に$x=a$を代入します。

$$
\begin{align}
f(a)
&\simeq
f(a)+pa^2+qa+r
\\\\
f'(a)
&\simeq
f'(a)+2pa+q
\\\\
f'{}'(a)
&\simeq
2p
\end{align}
$$

この3式より

$$
\begin{array}{l}
pa^2+qa+r=0
\\\\
2pa+q=0
\\\\
2p=f'{}'(a)
\end{array}
$$

を満たせば近似が成り立つので、これを解いて

$$
\begin{align}
p&=
\displaystyle\frac{1}{2}f'{}'(a)
\\\\
q&=
-af'{}'(a)
\\\\
r&=
\displaystyle\frac{1}{2}a^2f'{}'(a)
\end{align}
$$

よって

$$
px^2+qx+r
=
\displaystyle\frac{1}{2}f'{}'(a)(x-a)^2
$$

これを式(1)に代入して

$$
f(x)
\simeq
f(a)+f'(a)(x-a)+\displaystyle\frac{1}{2}f'{}'(a)(x-a)^2
$$

となります。これで2次式まで使った近似式ができました。

同じ要領で3次式も使った近似式を求めると

$$
f(x)
\simeq
f(a)+f'(a)(x-a)+\displaystyle\frac{1}{2}f'{}'(a)(x-a)^2
+
\displaystyle\frac{1}{6}f'{}'{}'(a)(x-a)^3
$$

こうなります。これを繰り返して$n$次式まで使うと

$$
f(x)
\simeq
\displaystyle\sum_{k=0}^n
\displaystyle\frac{1}{k!}
f^{(k)}(a)(x-a)^k
$$

となります。$n\to\infty$とすることで近似精度が高まり、もはや近似式ではなく等式になります。

$$
f(x)
=
\displaystyle\sum_{n=0}^\infty
\displaystyle\frac{1}{n!}
f^{(n)}(a)(x-a)^n
$$

この等式がテイラー展開の公式です。

近似精度の検証

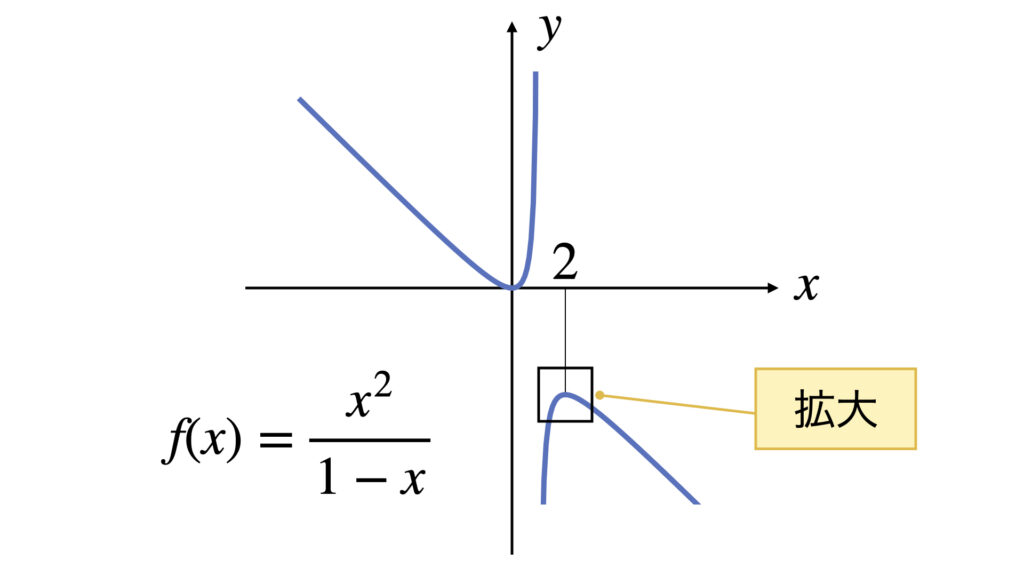
本当にテイラー展開の公式は近似できているのか、以下の関数で確かめてみましょう。

$$
f(x)
=
\displaystyle\frac{x^2}{1-x}
$$

この関数を$x=2$でテイラー展開します。

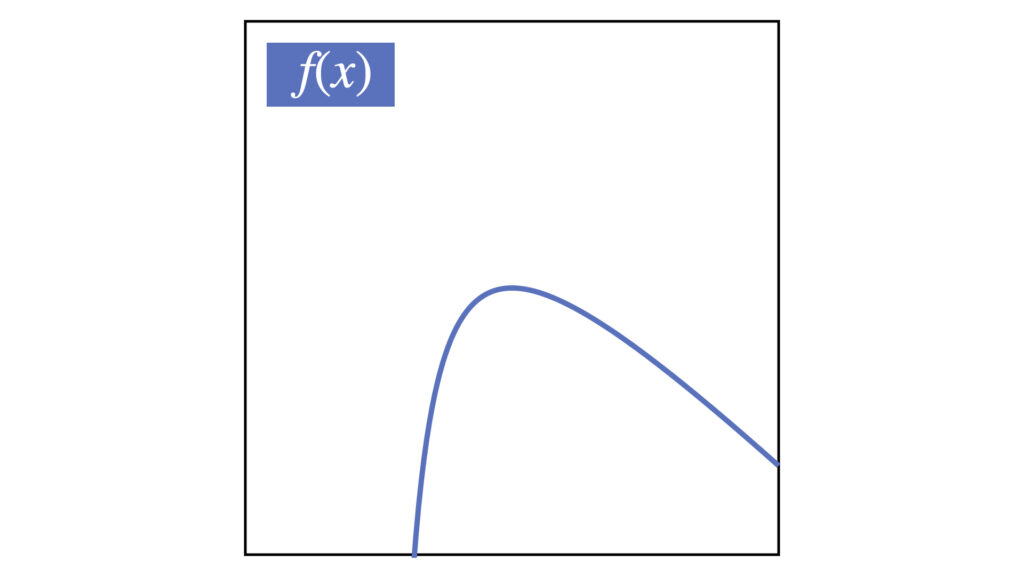
テイラー展開の準備

テイラー展開では$n$次導関数が必要なので、先に計算して準備しておきましょう。

$$
\begin{array}{ll}
f^{(n)}(x)
=
\displaystyle\frac{x(2-x)}{(1-x)^2}
&
(n=1)
\\\\
f^{(n)}(x)
=
n!(1-x)^{-n-1}
&
(n \geq 2)
\end{array}
$$

$n$次導関数の計算方法は$n$次導関数のページで解説していますのでご覧ください。

n次導関数の計算方法

n次導関数を計算する方法として、数学的帰納法とライプニッツの微分公式の2パターンを勉強します。テイラー展開の分野でn次導関数が必要になります。

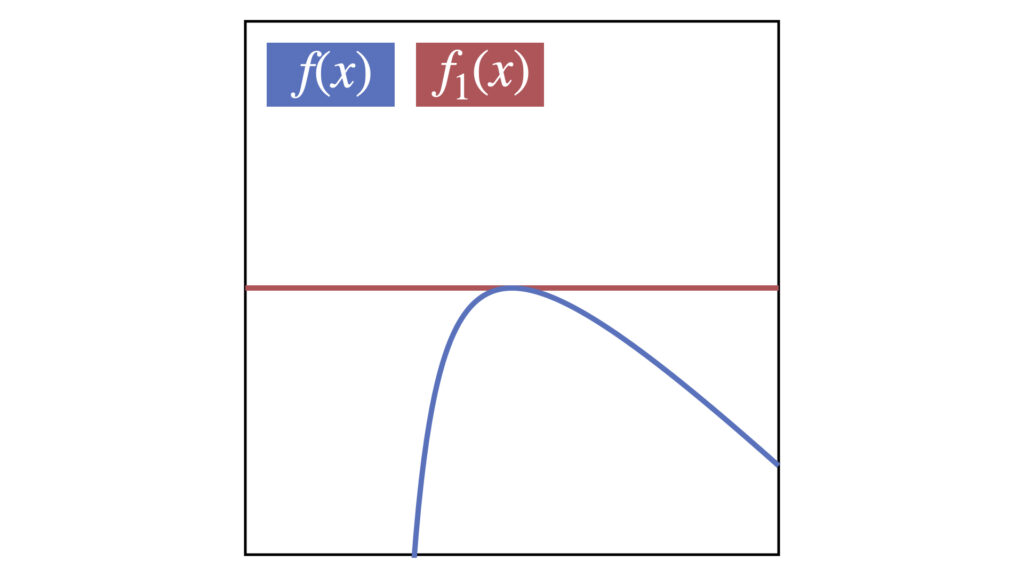
1次式で近似

$$
\begin{align}
f_1(x)
&=
\displaystyle\sum_{n=0}^1
\displaystyle\frac{1}{n!}
f^{(n)}(2)(x-2)^n
\\\\&=
f(2)+f^{(1)}(2)(x-2)
\\\\&=
-4
\end{align}
$$

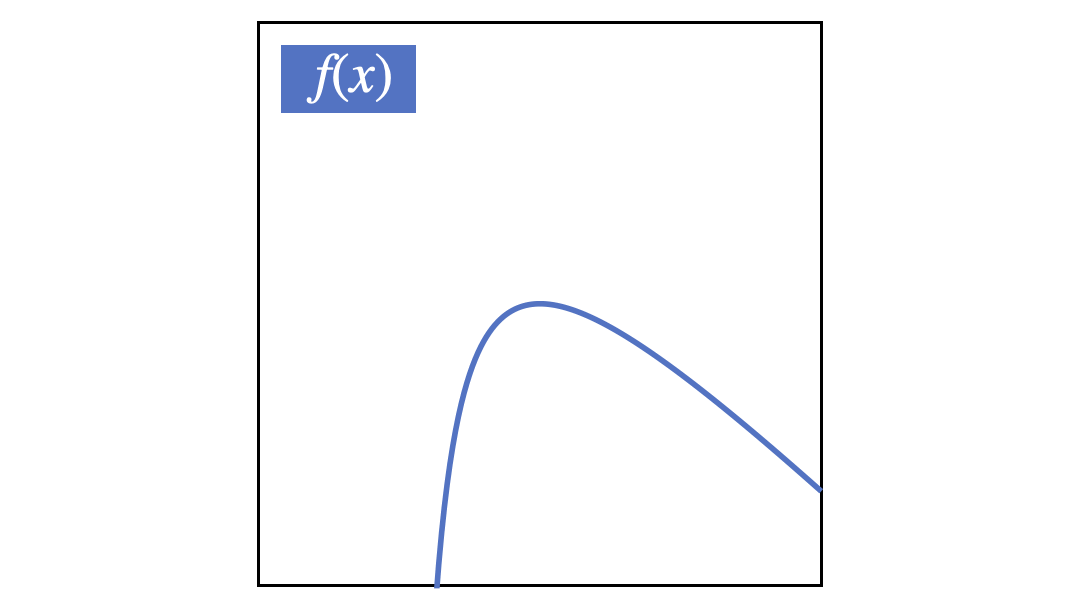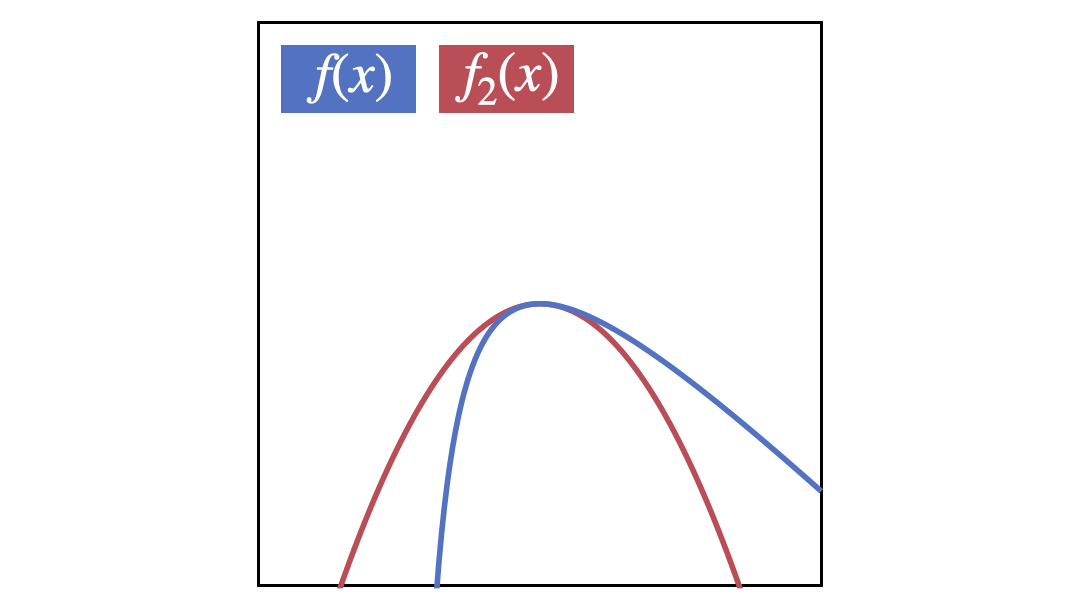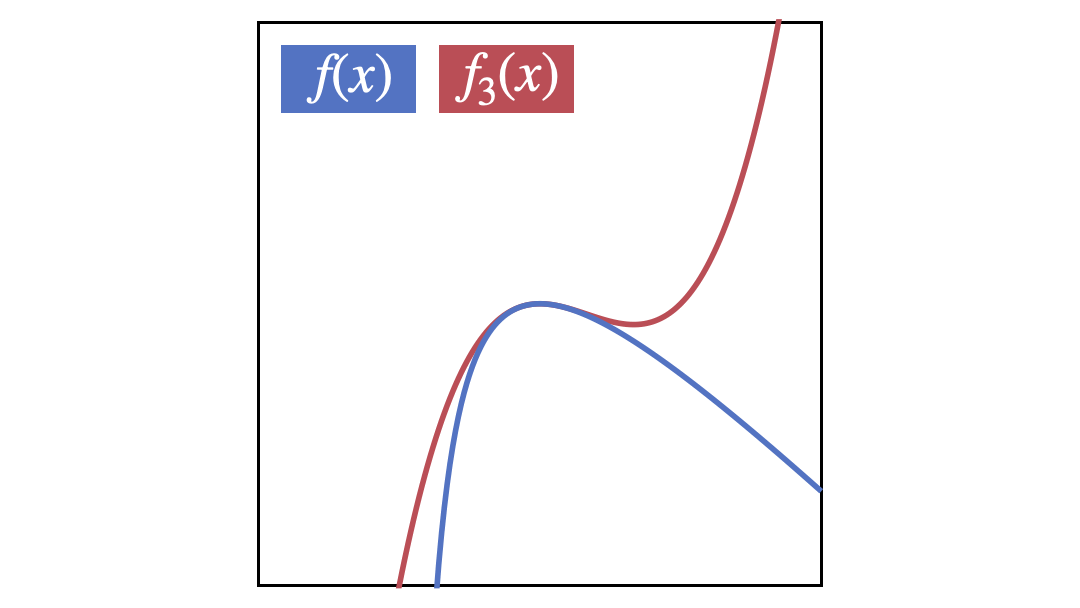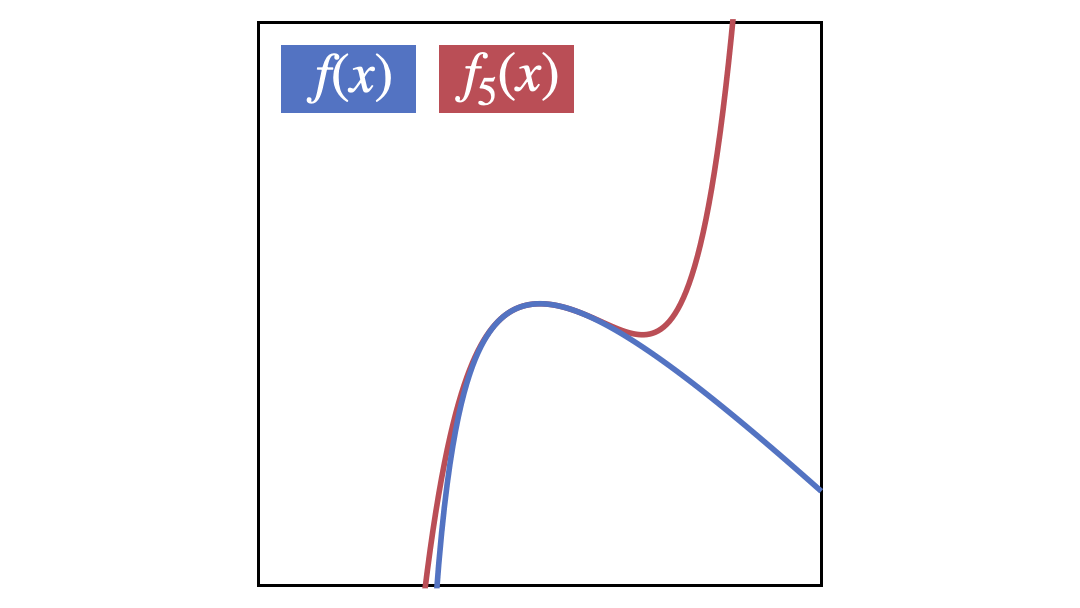
2次式で近似

$$
\begin{align}
f_2(x)
&=
\displaystyle\sum_{n=0}^2
\displaystyle\frac{1}{n!}
f^{(n)}(2)(x-2)^n
\\\\&=
f_1(x)+\displaystyle\frac{1}{2}f^{(2)}(2)(x-2)^2
\\\\&=
-x^2+4x-8
\end{align}
$$

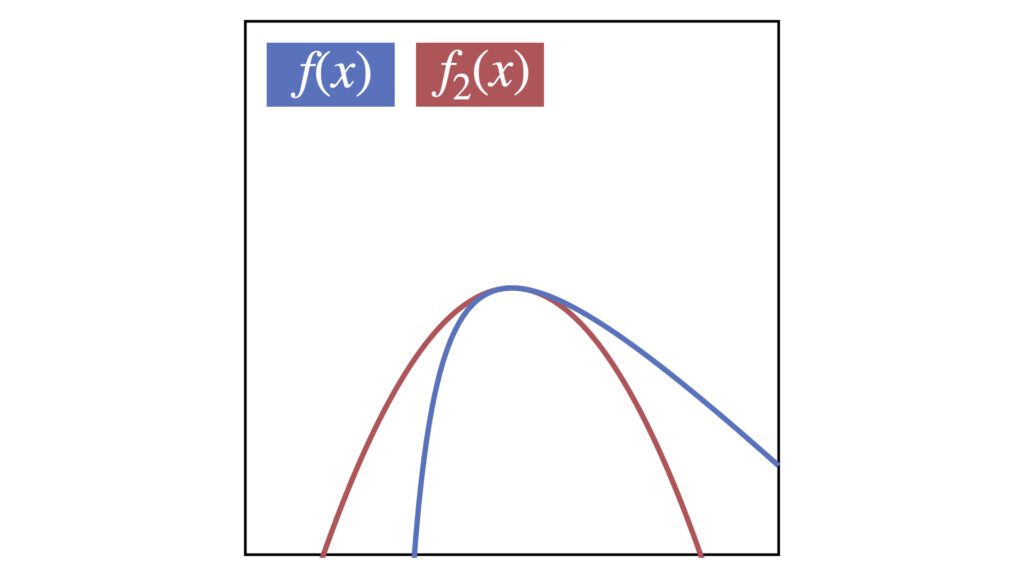
3次式で近似

$$
\begin{align}
f_3(x)
&=
\displaystyle\sum_{n=0}^3
\displaystyle\frac{1}{n!}
f^{(n)}(2)(x-2)^n
\\\\&=
f_2(x)+\displaystyle\frac{1}{6}f^{(3)}(2)(x-2)^3
\\\\&=
x^3-7x^2+16x-16
\end{align}
$$

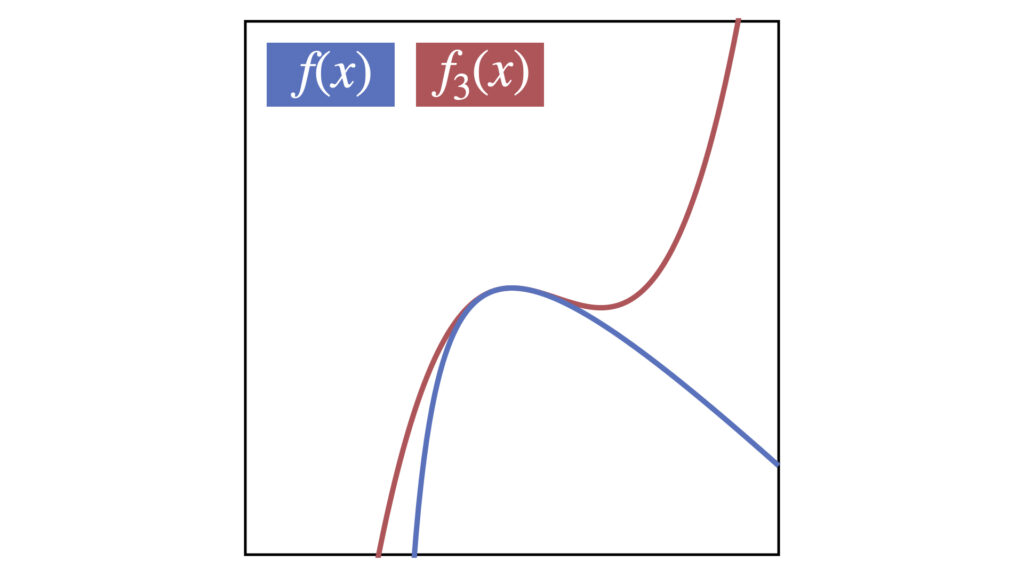
4次式で近似

$$
\begin{align}
f_4(x)
&=
\displaystyle\sum_{n=0}^4
\displaystyle\frac{1}{n!}
f^{(n)}(2)(x-2)^n
\\\\&=
f_3(x)+\displaystyle\frac{1}{24}f^{(4)}(2)(x-2)^4
\\\\&=
-x^4+9x^3-31x^2+48x-32
\end{align}
$$

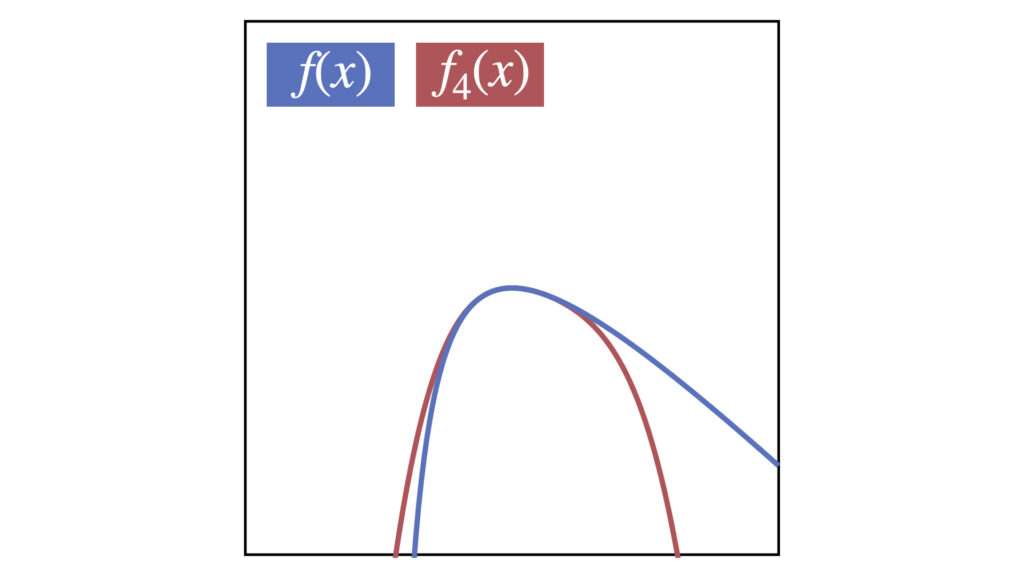
5次式で近似

$$
\begin{align}
f_5(x)
&=
\displaystyle\sum_{n=0}^5
\displaystyle\frac{1}{n!}
f^{(n)}(2)(x-2)^n
\\\\&=
f_4(x)+\displaystyle\frac{1}{120}f^{(5)}(2)(x-2)^5
\\\\&=
x^5-11x^4+49x^3-111x^2+128x-64
\end{align}
$$

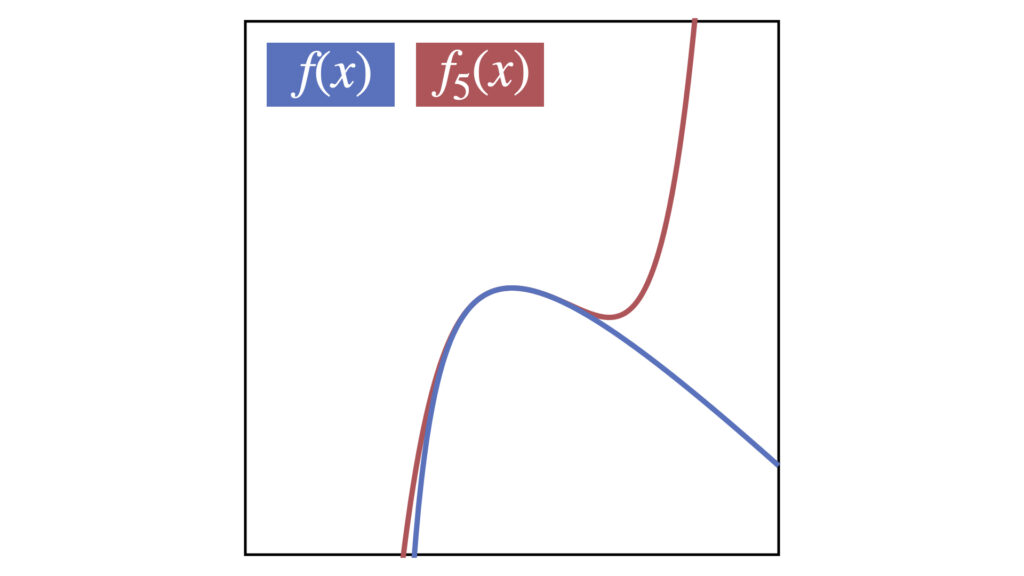
近似のGIF画像

$f_1$から$f_5$までを順番に表示するGIF画像です。徐々に近似精度が高くなっていることが分かると思います。

マクローリン展開との関係性

$x=0$でのテイラー展開をマクローリン展開と呼びます。

マクローリン展開の公式は以下の式です。

$$
f(x)
=
\displaystyle\sum_{n=0}^\infty
\displaystyle\frac{1}{n!}
f^{(n)}(0)x^n
$$

テイラー展開の公式に$a=0$を代入しただけです。

まとめ

テイラー展開の公式は以下の式です。