こんにちはコーヤです。
このページでは、ロピタルの定理の使用条件3つと使い方を勉強します。ロピタルは使用条件を満たしていることの確認が大変ですが、正攻法では解けない極限も計算できるようになります。
ロピタルの定理の概要
ロピタルの定理は関数の極限を計算するときに便利な定理で、以下の式が成り立ちます。
$$
\displaystyle\lim_{x \to p}
\displaystyle\frac{f(x)}{g(x)}
=
\displaystyle\lim_{x \to p}
\displaystyle\frac{f'(x)}{g'(x)}
$$
このように分母分子を微分しても極限の値が一致します。
もとの形では計算できなくても、微分すれば簡単に計算できる形になることがよくあります。
ロピタルの定理の威力
正攻法で関数の極限を求めるときは式変形に頭を使わないといけませんが、ロピタルの定理なら瞬殺できます。
この極限を例にしてロピタルの定理の威力を味わいましょう。
$$
\displaystyle\lim_{x \to \frac{1}{4}\pi}
\displaystyle\frac{\sin x -\cos x}{4x-\pi}
$$
この極限を正攻法で求めるには三角関数の合成に気付かなければいけません。
三角関数の合成で極限を求める方法は関数の極限のページをご覧ください。
ロピタルの定理を使えば、分母分子を微分するだけで求まります。
$$
\begin{align}
\displaystyle\lim_{x \to \frac{1}{4}\pi}
\displaystyle\frac{\sin x -\cos x}{4x-\pi}
&=
\displaystyle\lim_{x \to \frac{1}{4}\pi}
\displaystyle\frac{\cos x +\sin x}{4}
\\\\&=
\displaystyle\frac{\displaystyle\frac{1}{\sqrt{2}}+\displaystyle\frac{1}{\sqrt{2}}}{4}
\\\\&=
\displaystyle\frac{\sqrt{2}}{4}
\end{align}
$$
計算は楽になり、式変形に頭も使いません。これがロピタルの定理の威力です。
ロピタルの定理の注意ポイント
威力を知ってしまうと全ての極限計算をロピタルの定理で処理しようと思うようになりますが、ロピタルの定理が使えない関数もあります。
また例を挙げます。正攻法とロピタルの定理の両方で解いてみます。
$$
\displaystyle\lim_{x \to 0}
\displaystyle\frac{x^2+x+2}{x^2+1}
$$
まずは正攻法で解きます。単純に$x=0$を代入すれば解けます。
$$
\displaystyle\lim_{x \to 0}
\displaystyle\frac{x^2+x+2}{x^2+1}
=
2
$$
これをロピタルの定理で解いてみます。
$$
\begin{align}
\displaystyle\lim_{x \to 0}
\displaystyle\frac{x^2+x+2}{x^2+1}
&=
\displaystyle\lim_{x \to 0}
\displaystyle\frac{2x+1}{2x}
\\\\&=
\displaystyle\frac{1}{0}
\\\\&=
\infty
\end{align}
$$
正攻法で解いたときと答えが異なります。
このようにロピタルの定理が使えない関数なのに気付かずにロピタルの定理を使ってしまうと、間違った答えが出てきてしまいます。
ロピタルの定理の使用条件3つ
ロピタルの定理が使えるかどうかのチェックポイントは3つあります。
- 不定形であること
- 極限付近で$g'(x)\neq0$であること
- 微分後の極限が存在すること
それぞれ条件を見ていきましょう。
条件1. 不定形であること
まずは不定形であることを確かめないといけません。
$$
\displaystyle\lim_{x \to p}
\displaystyle\frac{f(x)}{g(x)}
=
\displaystyle\frac{0}{0}
$$
$$
\displaystyle\lim_{x \to p}
\displaystyle\frac{f(x)}{g(x)}
=
\displaystyle\frac{\pm \infty}{\pm \infty}
$$
このどちらかの形になっていないといけません。
冒頭の例は
$$
\displaystyle\lim_{x \to 0}
\displaystyle\frac{x^2+x+2}{x^2+1}
=
\displaystyle\frac{2}{1}
$$
このように不定形ではないのでロピタルの定理が使えません。
条件2. 極限付近で$g'(x)\neq0$であること
求めたい極限が$x\to a$のようにある実数$a$に近づく場合と、$x\to\infty$のように発散する場合で、極限付近の扱い方が異なります。
$x\to a$の極限の場合、極限付近は$i_1 < a < i_2$となる実数$i_1,i_2$を用いて、以下の画像で示す区間を極限付近の区間$I$として扱います。
$x\to\infty$の極限の場合、ある実数$m$を用いて、以下の画像で示す区間を極限付近の区間$M$として扱います。

$i_1,i_2,m$の値は自分の都合のいいように値を選んで大丈夫です。
逆に、どんな選び方をしても$g'(x)\neq0$となる極限付近の区間が設定できない場合、ロピタルの定理は使えません。
$g(x)=\cos x$の極限を例に区間を設定してみましょう。極限は$x \to 0$と$x \to \infty$の2つの場合を考えます。
$$
\begin{array}{ccc}
\displaystyle\lim_{x \to 0}
\displaystyle\frac{f(x)}{\cos x}
&
,
&
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{f(x)}{\cos x}
\end{array}
$$
下の図は$g'(x)=-\sin x = 0$となる点に黒丸をつけています。
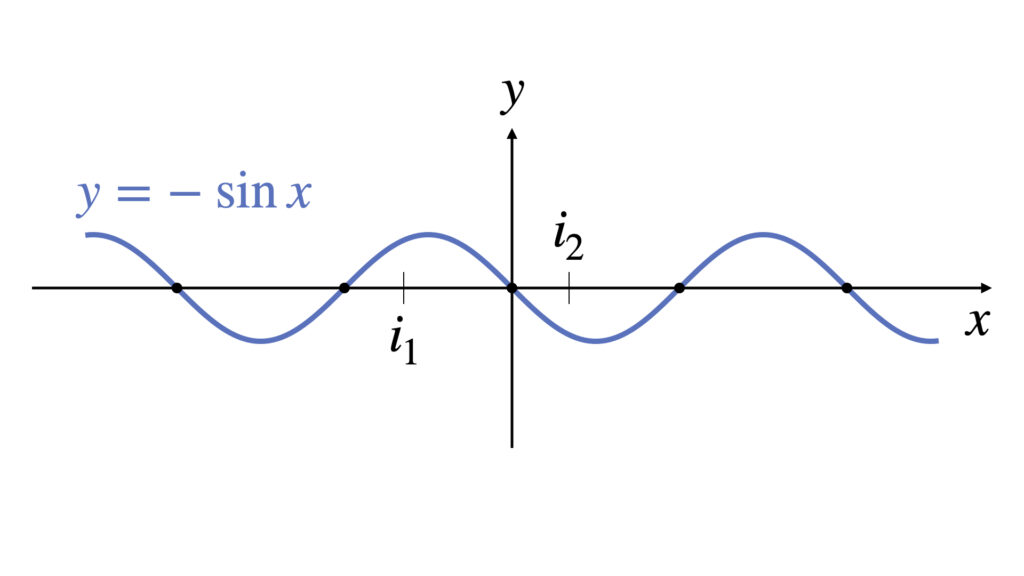
$x \to 0$の極限の場合、図に示したように$i_1$と$i_2$を設定すれば極限付近の区間$I$で$g'(x)=0$となる点が存在しなくなります。
$x \to \infty$の極限の場合、$m$の値をどこに設定しても区間$M$で$g'(x)=0$となる点が現れます。
これより、$g(x)=\cos x$かつ$x \to \infty$の極限はロピタルの定理が使えないということになります。
$x\to -\infty$の極限では区間$M=(-\infty,m)$となります。
$x\to -\infty$のときは$x=-t$として$t\to \infty$に変形したほうが分かりやすいかもしれません。
条件3. 微分後の極限が存在すること
ロピタルの定理の右辺、つまり微分した後の極限が存在しない場合はロピタルの定理は使えません。
$$
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{f'(x)}{g'(x)}
=
\displaystyle\lim_{x \to \infty}
\sin x
$$
例えば微分した計算結果が$\sin x$になった場合の極限は振動です。振動の場合は極限なしなので、ロピタルの定理は使えません。
ロピタルの定理が使えるのは収束する場合、発散する場合です。
ロピタルの定理が使えないのは振動する場合、右側極限と左側極限が異なる場合です。
ロピタルの定理の例題
それでは例題5つでロピタルの定理を使う練習をしましょう。
例題1
$$
\displaystyle\lim_{x \to 0}
\displaystyle\frac{x}{\sqrt{1+x}+\sqrt{1-x}}
$$
条件1の「不定形であること」を調べます。
$$
\displaystyle\lim_{x \to 0}
\displaystyle\frac{x}{\sqrt{1+x}+\sqrt{1-x}}
=
\displaystyle\frac{0}{2}
$$
不定形ではないのでロピタルの定理は使えません。
単純に代入するだけで答えが求まります。
$$
\displaystyle\lim_{x \to 0}
\displaystyle\frac{x}{\sqrt{1+x}+\sqrt{1-x}}
=
0
$$
例題2
$$
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{x}{(2x+\sin 2x)e^{\sin x}}
$$
条件1の「不定形であること」を調べます。
分子は$\infty$です。分母は不定形か怪しいので「はさみうち」で調べます。
$$
\displaystyle\frac{1}{e}
\leq
e^{\sin x}
\leq
e
$$
$$
-1
\leq
\sin 2x
\leq
1
$$
この2式より
$$
(2x-1)\displaystyle\frac{1}{e}
\leq
(2x+\sin 2x)e^{\sin x}
\leq
(2x+1)e
$$
両サイドはどちらも
$$
\displaystyle\lim_{x \to \infty}
(2x-1)\displaystyle\frac{1}{e}
=
\displaystyle\lim_{x \to \infty}
(2x+1)e
=
\infty
$$
となるので
$$
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{x}{(2x+\sin 2x)e^{\sin x}}
=
\displaystyle\frac{\infty}{\infty}
$$
と不定形になります。
条件2の「極限付近で$g'(x)\neq0$であること」を調べます。
$$
g(x)
=
(2x+\sin 2x)e^{\sin x}
$$
より
$$
\begin{align}
g'(x)
&=
\left( 2+2\cos 2x \right)e^{\sin x}+\left( 2x+\sin 2x \right)e^{\sin x}\cos x
\\\\&=
\left( 2+4\cos^2 x-2 \right)e^{\sin x}+\left( 2x+\sin 2x \right)e^{\sin x}\cos x
\\\\&=
4\cos ^2 x e^{\sin x}+(2x+\sin 2x)e^{\sin x}\cos x
\\\\&=
e^{\sin x}\cos x(4\cos x+2x+\sin 2x)
\end{align}
$$
分母に$\cos x$があります。したがって極限付近の区間$(m,\infty)$において、$m$の値をどこに設定しても$m$より大きい場所で$g'(x)=0$となる点は周期的に現れます。
これよりロピタルの定理は使えません。
代わりに正攻法で解きます。
$$
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{x}{(2x+\sin 2x)e^{\sin x}}
=
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{x}{2x+\sin 2x}
\cdot
\displaystyle\frac{1}{e^{\sin x}}
$$
この2つに分解して考えます。まずは左側から
$$
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{x}{2x+1}
\leq
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{x}{2x+\sin 2x}
\leq
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{x}{2x-1}
$$
この「はさみうち」より
$$
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{x}{2x+\sin 2x}
=
\displaystyle\frac{1}{2}
$$
となります。
次に右側です。
$$
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{1}{e^{\sin x}}
$$
これは振動です。
以上の結果より
$$
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{x}{(2x+\sin 2x)e^{\sin x}}
$$
は振動です。極限なしとなります。
例題3
$$
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{x-\cos x}{x}
$$
条件1の「不定形であること」を調べます。
$\cos x$が振動しているので「はさみうち」で処理しましょう。
$$
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{x-1}{x}
\leq
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{x-\cos x}{x}
\leq
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{x+1}{x}
$$
両サイドはどちらも
$$
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{x-1}{x}
=
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{x+1}{x}
=
\displaystyle\frac{\infty}{\infty}
$$
となるので
$$
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{x-\cos x}{x}
=
\displaystyle\frac{\infty}{\infty}
$$
です。
条件2の「極限付近で$g'(x)\neq0$であること」を調べます。
$$
g(x)
=
x
$$
より
$$
g'(x)
=
1
$$
です。
したがって極限付近の区間$(m,\infty)$において、$m$の値をどんな値に設定しても$g'(x)=0$となる点は現れません。
条件3の「微分後の極限が存在すること」を調べます。
$$
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{1-\sin x}{1}
=
\displaystyle\lim_{x \to \infty}
1-\sin x
$$
これは振動です。極限なしとなります。
微分後の極限が存在しないため、ロピタルの定理は使えません。
代わりに正攻法で解きます。分母分子を$x$で割って
$$
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{x-\cos x}{x}
=
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{1-\displaystyle\frac{\cos x}{x}}{1}
$$
さらに「はさみうち」を用いて
$$
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{-1}{x}
\leq
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{\cos x}{x}
\leq
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{1}{x}
$$
両サイドを計算して
$$
0
\leq
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{\cos x}{x}
\leq
0
$$
以上より
$$
\displaystyle\lim_{x \to \infty}
\displaystyle\frac{1-\displaystyle\frac{\cos x}{x}}{1}
=
1
$$
です。
例題4
$$
\displaystyle\lim_{x \to 0}
\displaystyle\frac{\tanh(\arcsin x)}{x}
$$
この形のままロピタルの定理が使えるかどうか調べるのは面倒なので、慣れ親しんだ関数へ変形してからにしましょう。
$\arcsin x=t$とおいて$t \to\infty$の極限に変形します。
$$
\begin{align}
\displaystyle\lim_{x \to 0}
\displaystyle\frac{\tanh(\arcsin x)}{x}
&=
\displaystyle\lim_{t \to 0}
\displaystyle\frac{\tanh t}{\sin t}
\\\\&=
\displaystyle\lim_{t \to 0}
\displaystyle\frac{e^t-e^{-t}}{\left(e^t+e^{-t}\right)\sin t}
\\\\&=
\displaystyle\lim_{t \to 0}
\displaystyle\frac{e^{2t}-1}{\left(e^{2t}+1\right)\sin t}
\end{align}
$$
この形でロピタルの定理が使えるか調べていきます。
条件1の「不定形であること」を調べます。
$$
\begin{align}
\displaystyle\lim_{t \to 0}
\displaystyle\frac{e^{2t}-1}{\left(e^{2t}+1\right)\sin t}
=
\displaystyle\frac{0}{0}
\end{align}
$$
不定形です。
条件2の「極限付近で$g'(x)\neq0$であること」を調べます。
$$
g(t)
=
\left(e^{2t}+1\right)\sin t
$$
より
$$
\begin{align}
g'(t)
&=
2e^{2t}\sin t + \left( e^{2t}+1 \right)\cos t
\\\\&=
\sqrt{5e^{4t}+2e^{2t}+1}
\sin
\left(
t+
\arctan
\displaystyle\frac{e^{2t}+1}{2e^{2t}}
\right)
\end{align}
$$
この式変形は三角関数の合成を使いました。
$g'(t)$のグラフを書くのは無理そうですが、今は$t\to\ 0$の付近で$g'(t)\neq0$であること調べればいいだけです。
$t=0$を代入して
$$
\begin{align}
g'(0)
&=
\sqrt{8}
\sin
(\arctan 1)
\\\\&=
2\sqrt{2}
\sin
\displaystyle\frac{1}{4}\pi
\\\\&=
2
\end{align}
$$
となります。$t=0$で$g'(t)\neq0$であることは分かりました。
極限付近の区間の設定ですが、グラフが書けないのでテキトーに$i_1=-0.00001,$$i_2=0.00001$みたいな感じで設定します。
こうすれば$t \to 0$のとき、区間$(i_1,0)\cup(0,i_2)$で$g'(t)=0$となる点が存在しなくなります。
条件3の「微分後の極限が存在すること」を調べます。
$$
\begin{align}
\displaystyle\lim_{t \to 0}
\displaystyle\frac{2e^{2t}}
{
\sqrt{5e^{4t}+2e^{2t}+1}
\sin
\left(
t+
\arctan
\displaystyle\frac{e^{2t}+1}{2e^{2t}}
\right)
}
&=
\displaystyle\frac{2}{2}
\\\\&=
1
\end{align}
$$
微分後の極限が存在します。
使用条件3つをクリアしたので、ロピタルの定理が使えることが分かりました。
微分後の極限は既に条件3で求めているので、もとの極限も
$$
\displaystyle\lim_{t \to 0}
\displaystyle\frac{e^{2t}-1}{\left(e^{2t}+1\right)\sin t}
=
1
$$
となります。したがって式変形する前の極限も
$$
\displaystyle\lim_{x \to 0}
\displaystyle\frac{\tanh(\arcsin x)}{x}
=
1
$$
となります。
関数の極限のページでは同じ問題を正攻法で解いていますので、計算過程を見比べてみてください。
ロピタルの定理は一見便利なように思えますが、正攻法で解ける問題は正攻法で解いた方がよっぽど楽です。
例題5
$$
\displaystyle\lim_{x \to 0}
\left(
\displaystyle\frac{\sin x}{x}
\right)
^{\frac{1}{x^2}}
$$
ロピタルの定理を使うために分数の形に分解します。
$$
\displaystyle\lim_{x \to 0}
\left(
\displaystyle\frac{\sin x}{x}
\right)
^{\frac{1}{x^2}}
=
\displaystyle\lim_{x \to 0}
\displaystyle\frac{\sin ^{\frac{1}{x^2}}x}{x^{\frac{1}{x^2}}}
$$
ロピタルの定理が使えるかを調べるのはちょっと面倒な形です。
ゴリ押しで調べてもOKですが、正攻法で式変形して単純な形にならないか試してみましょう。
$1+t=\displaystyle\frac{\sin x}{x}$として$t\to 0$の極限に変形します。
$$
\begin{align}
\displaystyle\lim_{x \to 0}
\left(
\displaystyle\frac{\sin x}{x}
\right)
^{\frac{1}{x^2}}
&=
\displaystyle\lim_{t \to 0}
(1+t)
^{\frac{1}{x^2}}
\\\\&=
\displaystyle\lim_{t \to 0}
\left\{
(1+t)
^{\frac{1}{t}}
\right\}
^{\frac{t}{x^2}}
\\\\&=
\displaystyle\lim_{t \to 0}
e^{\frac{t}{x^2}}
\end{align}
$$
ここで$\displaystyle\frac{t}{x^2}$について詳しく見ていきます。
$$
\begin{align}
\displaystyle\lim_{t \to 0}
\displaystyle\frac{t}{x^2}
&=
\displaystyle\lim_{x \to 0}
\displaystyle\frac{\displaystyle\frac{\sin x}{x}-1}{x^2}
\\\\&=
\displaystyle\lim_{x \to 0}
\displaystyle\frac{\sin x-x}{x^3}
\end{align}
$$
ロピタルの定理が使えそうな形がでてきました。
条件1の「不定形であること」を調べます。
$$
\displaystyle\lim_{x \to 0}
\displaystyle\frac{\sin x-x}{x^3}
=
\displaystyle\frac{0}{0}
$$
不定形です。
条件2の「極限付近で$g'(x)\neq0$であること」を調べます。
$$
g(x)
=
x^3
$$
より
$$
g'(x)
=
3x^2
$$
$g'(x)=0$になるのは$x=0$のときだけです。
これより$i_1,i_2$は$i_1<0<i_2$を満たすテキトーな値に設定します。
こうすれば$x \to 0$のとき、区間$(i_1,0)\cup(0,i_2)$で$g'(x)=0$となる点が存在しなくなります。
条件3の「微分後の極限が存在すること」を調べます。
$$
\begin{align}
\displaystyle\lim_{x \to 0}
\displaystyle\frac{\cos x-1}{3x^2}
&=
\displaystyle\frac{1-\cos x}{x^2}
\cdot
\displaystyle\frac{-1}{3}
\\\\&=
\displaystyle\frac{1}{2}
\cdot
\displaystyle\frac{-1}{3}
\\\\&=
-\displaystyle\frac{1}{6}
\end{align}
$$
微分後の極限が存在します。
使用条件3つをクリアしたので、ロピタルの定理が使えることが分かりました。
微分後の極限は既に条件3で求めているので、もとの極限も
$$
\displaystyle\lim_{x \to 0}
\displaystyle\frac{\sin x-x}{x^3}
=
-\displaystyle\frac{1}{6}
$$
となります。この結果を代入して
$$
\begin{align}
\displaystyle\lim_{x \to 0}
\left(
\displaystyle\frac{\sin x}{x}
\right)
^{\frac{1}{x^2}}
&=
\displaystyle\lim_{t \to 0}
e^{\frac{t}{x^2}}
\\\\&=
e^{-\frac{1}{6}}
\end{align}
$$
となります。
まとめ
ロピタルの定理が使えるかどうかのチェックポイントは3つあります。
- 不定形であること
- 極限付近で$g'(x)\neq0$であること
- 微分後の極限が存在すること
これらを満たした場合、以下のロピタルの定理が成り立ちます。
$$
\displaystyle\lim_{x \to p}
\displaystyle\frac{f(x)}{g(x)}
=
\displaystyle\lim_{x \to p}
\displaystyle\frac{f'(x)}{g'(x)}
$$




コメント欄