こんにちはコーヤです。
このページでは、多変数関数に含まれる変数のうちの1つ変数に注目して微分する、偏微分の意味と計算方法を勉強します。
※普通の微分と偏微分を区別するために、普通の微分のことを「常微分」と記載します。
常微分と偏微分の違い
常微分と比べながら偏微分の意味を確認します。
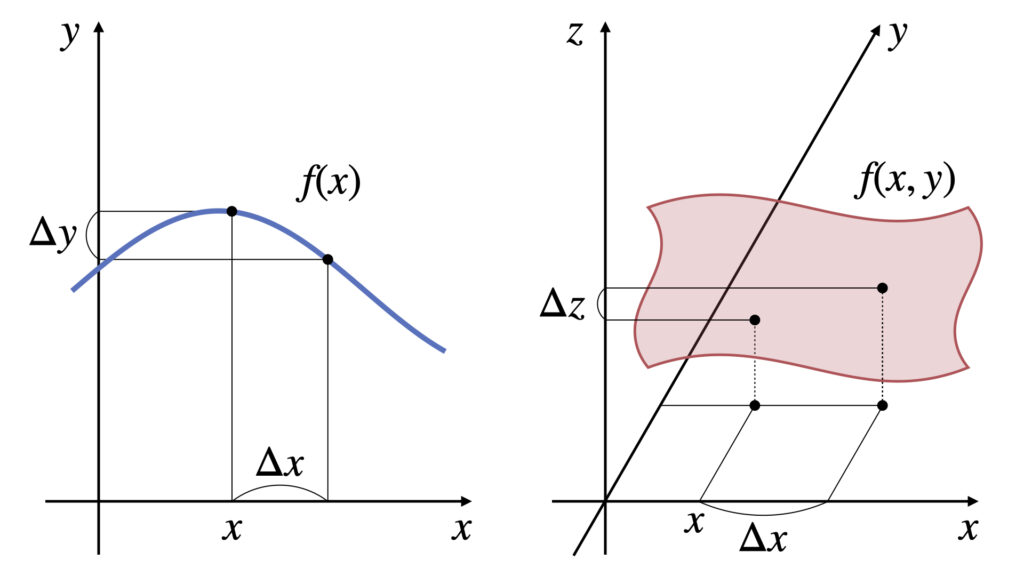
常微分の意味
$x$が$\Delta x$だけ変化した時の$y$の変化量$\Delta y$は
$$
\Delta y
=
f(x+\Delta x)-f(x)
$$
なので、平均変化率は
$$
\displaystyle\frac{\Delta y}{\Delta x}
=
\displaystyle\frac{f(x+\Delta x)-f(x)}{\Delta x}
$$
であり、ここで$\Delta x \to 0$のとき
$$
\displaystyle\frac{dy}{dx}
=
\displaystyle\lim_{\Delta x \to 0}
\displaystyle\frac{f(x+\Delta x)-f(x)}{\Delta x}
$$
となる。
偏微分の意味
$x$が$\Delta x$だけ変化した時の$z$の変化量$\Delta z$は
$$
\Delta z
=
f(x+\Delta x,y)-f(x,y)
$$
なので、平均変化率は
$$
\displaystyle\frac{\Delta z}{\Delta x}
=
\displaystyle\frac{f(x+\Delta x,y)-f(x,y)}{\Delta x}
$$
であり、ここで$\Delta x \to 0$のとき
$$
\displaystyle\frac{\partial z}{\partial x}
=
\displaystyle\lim_{\Delta x \to 0}
\displaystyle\frac{f(x+\Delta x,y)-f(x,y)}{\Delta x}
$$
となる。
偏微分の意味は以上です。常微分と同じ計算です。
偏微分の表現方法
偏微分には$\partial$という記号を使います。常微分の$d$に当たる記号で、「常微分ではなく偏微分をしている」ことを表すために$d$から$\partial$に変えています。
読み方はデル、ラウンド、ラウンドディー、パーシャル、など様々ありますので、好きな呼び方で呼んでください。

$dx$の「ディーエックス」と同じように$\partial x$は「デルエックス」と言うのが一般的かと思います。
1変数関数$f(x)$の導関数の表現方法は下のように様々な方法がありました。
$$
\begin{array}{ccccc}
f'(x)
& , &
\displaystyle\frac{df}{dx}
& , &
\displaystyle\frac{d}{dx}f(x)
\end{array}
$$
同様に2変数関数$f(x,y)$の偏導関数の表現方法は下のように様々な方法があります。上段が$x$での偏微分、下段が$y$での偏微分です。
$$
\begin{array}{ccccc}
f_x(x,y)
& , &
\displaystyle\frac{\partial f}{\partial x}
& , &
\displaystyle\frac{\partial}{\partial x}f(x,y)
\\\\
f_y(x,y)
& , &
\displaystyle\frac{\partial f}{\partial y}
& , &
\displaystyle\frac{\partial}{\partial y}f(x,y)
\end{array}
$$
偏微分計算の例題
それでは例題で偏微分の計算をしてみましょう。
以下の関数の2階偏導関数まで求めます。
$$
f(x,y)
=
x^3+y^2+\sin(xy)
$$
まず1階偏導関数を求めます。$x$での偏微分と$y$での偏微分の2種類があります。
$$
\begin{align}
f_x(x,y)
&=
3x^2+y\cos(xy)
\\\\
f_y(x,y)
&=
2y+x\cos(xy)
\end{align}
$$
偏微分と関係ない方の変数は定数とみなして常微分計算すればOKです。
次に2階偏導関数を求めます。$f_x$の$x$での偏微分と$y$での偏微分の2種類、$f_y$の$x$での偏微分と$y$での偏微分の2種類で、計4種類あります。
$$
\begin{align}
f_{xx}(x,y)
&=
6x-y^2\sin(xy)
\\\\
f_{xy}(x,y)
&=
\cos(xy)-xy\sin(xy)
\\\\
f_{yx}(x,y)
&=
\cos(xy)-xy\sin(xy)
\\\\
f_{xx}(x,y)
&=
2-x^2\sin(xy)
\end{align}
$$
となります。
$f_{xy}$は$f_x$を$y$で偏微分した関数です。
$$
f_{xy}
=
(f_x)_y
=
\displaystyle\frac{\partial}{\partial y}f_x
$$
こんな感じのイメージです。
この例でも分かる通り偏微分の計算自体は常微分計算と同じです。気楽に計算しましょう。
シュワルツの定理
シュワルツの定理の概要
偏微分の順番を入れ替えてもOKかどうかを判断するシュワルツの定理という定理があります。
上記の例題でも
$$
f_{xy}=f_{yx}
$$
となっていたように、例題の$f(x,y)$は$x$と$y$のどちらから先に偏微分しても偏導関数は一致します。つまり偏微分の順番を勝手に入れ替えてもOKということです。
逆に言うと、偏微分の順番を入れ替えたらいけない関数もあります。これを判断するのがシュワルツの定理です。
シュワルツの定理の具体例
$f(x,y)$が$C^2$級の関数なら以下の式が成り立ちます。
$$
f_{xy}=f_{yx}
$$
$C^2$級は関数の滑らかさを表す表現方法です。
$f(x,y)$が$C^2$級であるためには、2階偏導関数$f_{xx},f_{xy},f_{yx},f_{yy}$が存在し、かつ2階偏導関数4つとも連続である必要があります。
$C^n$級の意味の詳細は解析関数のページをご覧ください。
$f(x,y)$が$C^3$級の関数なら以下の式が成り立ちます。
$$
\begin{align}
f_{xxy}=f_{xyx}=f_{yxx}
\\\\
f_{xyy}=f_{yxy}=f_{yyx}
\end{align}
$$
一般化すると「$f(x,y)$が$C^n$級の関数なら$n$階偏微分の順番を入れ替えてもOK」ということです。
まとめ
偏微分は多変数関数に含まれる変数のうちの1つ変数に注目して微分します。計算方法は常微分と同じです。






コメント欄